廣告倒排服務(wù)極致優(yōu)化

作者：百度Geek說 2023-01-03 09:33:56

漏斗優(yōu)化是檢索系統(tǒng)不變的話題，過去一年來，廣告漏斗優(yōu)化一改往日做“加法”，而通過簡化漏斗，提升全系統(tǒng)一致性。如百度這樣龐大的廣告庫規(guī)模、高流量規(guī)模以及復(fù)雜的業(yè)務(wù)規(guī)則，要做到極簡的漏斗層次，需要最高效的策略設(shè)計(jì)和最極致的工程實(shí)現(xiàn)。

1、業(yè)務(wù)背景 - 全系統(tǒng)Limitless

大家都清楚，廣告漏斗包括召回、粗排、精排這三部分，理想中的漏斗上寬下窄很規(guī)整，而現(xiàn)實(shí)中因?yàn)榉N種原因，漏斗已經(jīng)略顯飄逸了，這種不一致性會(huì)帶來很多業(yè)務(wù)繼續(xù)發(fā)展的復(fù)雜度。我們希望達(dá)到：模型一致，精簡漏斗，全系統(tǒng)Limitless。

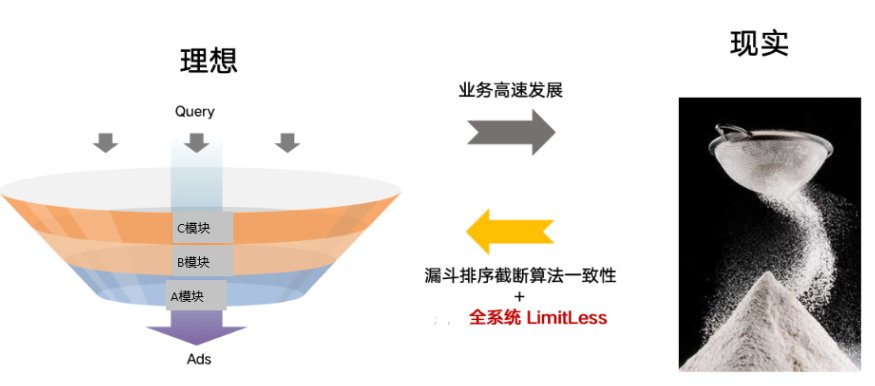
我們對(duì)Limitless的認(rèn)識(shí)：細(xì)節(jié)處見真章，挑戰(zhàn)軟件工程性能極限，方能漏斗近似無截?cái)唷?/p>

今天想跟大家聊聊『BS Limitless』項(xiàng)目里我們?cè)趺磽讣?xì)節(jié)的，整個(gè)項(xiàng)目其實(shí)挑戰(zhàn)很大，網(wǎng)絡(luò)、計(jì)算和存儲(chǔ)方方面面都涉及到，一篇短文很難講透，因此我決定選一個(gè)數(shù)據(jù)結(jié)構(gòu)-倒排表，讓大家感受到『極致』優(yōu)化。

2、技術(shù)背景 - 倒排表

先介紹一下優(yōu)化前的倒排表，它的組成比較經(jīng)典特點(diǎn)，HashMap<keysign, SkipList>。一次檢索pv根據(jù)觸發(fā)的N個(gè)詞（keysign）掃描拉鏈（SkipList），廣告業(yè)務(wù)投放特點(diǎn)天然會(huì)有長鏈、超長鏈，為此鏈表需要有序，做過漏斗的同學(xué)知道，在倒排階段排序能用的信息其實(shí)是很少的，這也說明了掃描Limitless對(duì)業(yè)務(wù)的高價(jià)值。

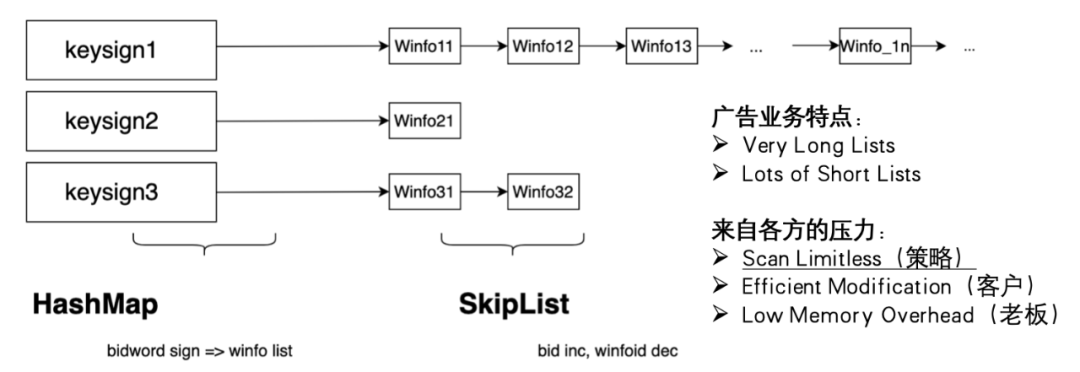
這樣一個(gè)小小的數(shù)據(jù)結(jié)構(gòu)承擔(dān)了各方的要求，1、讀性能決定有限時(shí)間能放出多少量，2、實(shí)時(shí)插入決定客戶投放能不能立即生效，3、單庫規(guī)模巨大，內(nèi)存損耗要低。對(duì)工程的合理要求，確實(shí)是既要...又要...還要...。在Limitless的大背景下，我們要顯著提升1達(dá)到scan limitless，但是不能損害到2和3。

回過頭來看，這么簡單的數(shù)據(jù)結(jié)構(gòu)，Limitless的瓶頸到底是什么？大家回憶一下計(jì)算機(jī)體系結(jié)構(gòu)的內(nèi)容。cpu并不直接訪存，而通過層層緩存到達(dá)內(nèi)存，存儲(chǔ)層次越低，它的容量越大但延遲越高，mem和L2、L1之間有量級(jí)差距[1]。List這種數(shù)據(jù)結(jié)構(gòu)顯然缺乏空間局部性。

緩存不親和的List對(duì)比緩存友好的Array，在掃描上究竟有多差呢？我們做了如下的評(píng)測，其中橫軸代表鏈長或數(shù)組長度，縱軸是平均到單條元素的掃描耗時(shí)，結(jié)果是10+差距。換成數(shù)組Array，也是不行的，客戶要求實(shí)時(shí)生效，為了低效拷貝損耗需要O(2N)的增長速度，內(nèi)存成本要求也不能滿足。

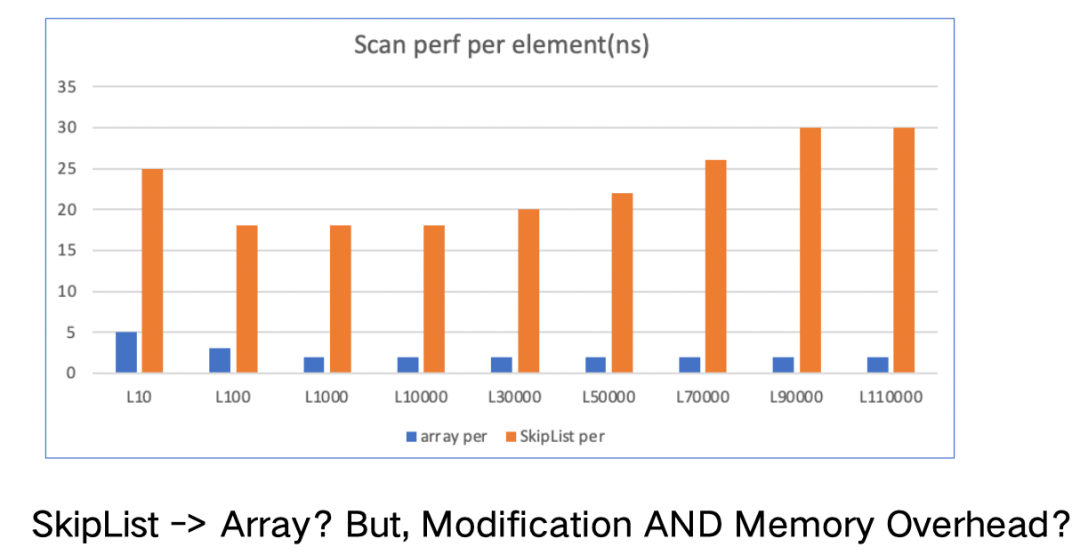
3、方案 - HybridIndexTable

我們針對(duì)業(yè)務(wù)的特點(diǎn)和Limitless的要求進(jìn)行極致設(shè)計(jì)和優(yōu)化，推出了新一代的內(nèi)存數(shù)據(jù)結(jié)構(gòu)HybridIndexTable，簡稱HIT。升級(jí)后的倒排表：

用HashMap索引keysign，
短鏈采用連續(xù)存儲(chǔ)，長鏈則是一棵葉子連續(xù)存儲(chǔ)的前綴樹，前綴樹則參考了業(yè)界AdaptiveRadixTree，簡稱ART，
短鏈和葉子的）連續(xù)存儲(chǔ)都采用了自研的RowContainer，簡稱RC。?

在簡短的數(shù)據(jù)結(jié)構(gòu)之外，還要和大家分享兩個(gè)關(guān)鍵細(xì)節(jié)：

Key序路由兜底超長鏈有序，
RC間無序，以RC為單位掃描。

HIT這樣的數(shù)據(jù)結(jié)構(gòu)有如下三點(diǎn)優(yōu)勢，恰到好處地滿足了前面的三個(gè)要求。

讀取性能高，連續(xù)存儲(chǔ)+前綴樹降低cachemiss，線程安全做法reader-friendly，還有面向負(fù)載的優(yōu)化；

更新時(shí)效性高，連續(xù)存儲(chǔ)但append-only/mark-delete；

內(nèi)存損耗少，應(yīng)用了大量的自適應(yīng)算法。

HIT上線后拿到了非常可觀的業(yè)務(wù)收益，Limitless的道路上技術(shù)就是生產(chǎn)力！

4、HIT緣起，內(nèi)存索引ModernCPU的探索

內(nèi)存索引領(lǐng)域已在面向Modern Cpu深耕，ModernCpu由于Cpu運(yùn)行得很快，使得緩存一致性的影響、訪存的影響成為高性能的瓶頸。內(nèi)存索引在2000s也有些階段性的標(biāo)志成果，包括FAST[4]，它是面向體系結(jié)構(gòu)的數(shù)據(jù)結(jié)構(gòu)設(shè)計(jì)的典型，無論是思想還是成果非常適用于靜態(tài)數(shù)據(jù)；CSBtree[2][3]，它提出數(shù)據(jù)結(jié)構(gòu)上通過KV分離，使得一次訪存能比較多個(gè)Key，同時(shí)還提出了SMO的無鎖解法；還有ART前綴樹[5]。有序索引中BTree居多，我們?yōu)楹巫⒁獾搅饲熬Y樹呢？

鏈表類型的緩存失效發(fā)生在每次訪問下一個(gè)節(jié)點(diǎn)，緩存失效復(fù)雜度O(n)。排序樹類型的緩存失效發(fā)生在訪問下一層節(jié)點(diǎn)，緩存失效復(fù)雜度O(lgn)。而對(duì)于前綴樹來說，緩存失效只和鍵長k(len)/扇出s(pan) 有關(guān)，緩存失效復(fù)雜度O(k/s)。如下圖[5]，假設(shè)k是鍵長的bit數(shù)，隨著存儲(chǔ)數(shù)據(jù)量上漲2^(k/8)、2^(k/4)、...，完全平衡樹高不斷增加，分別是k/8、k/4、...，而對(duì)于一顆前綴樹，樹高對(duì)于給定的span是恒定的，如針對(duì)span=8和4，樹高分別是k/8、k/4。前綴樹更加緩存友好。

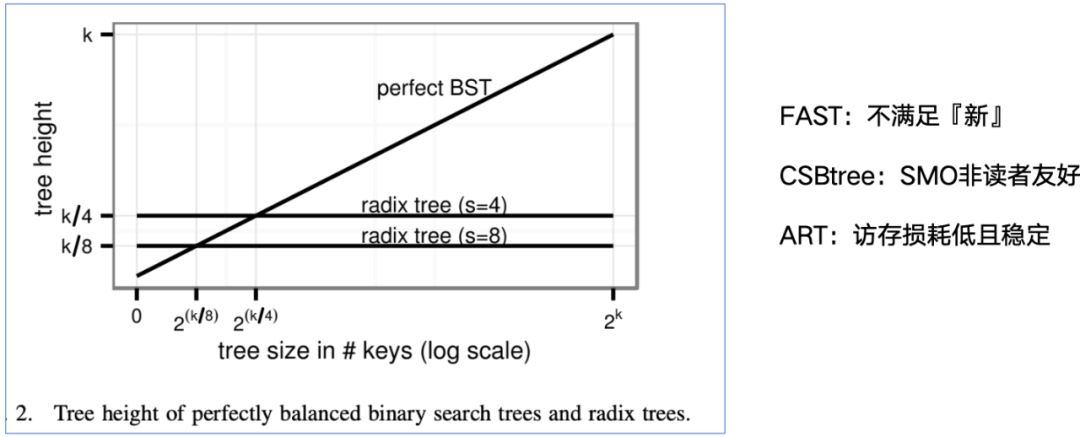
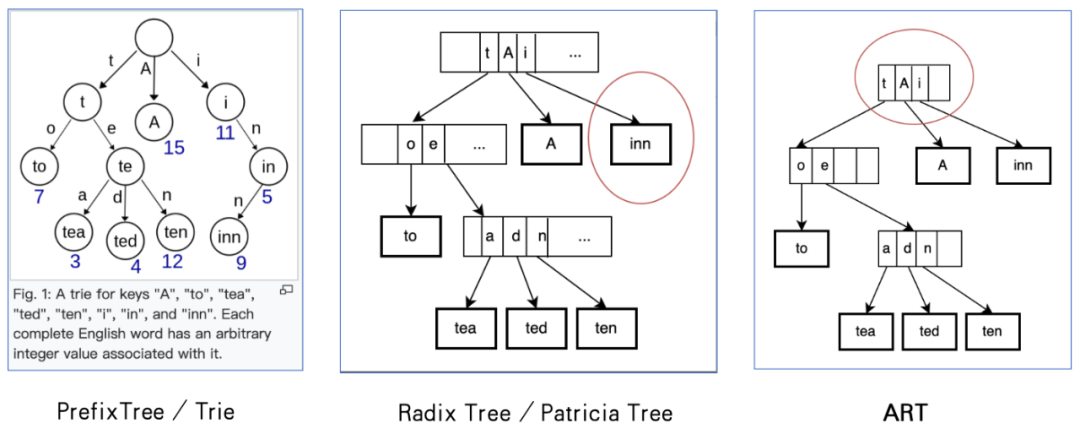
這里簡單介紹下前綴樹，英文是Trie、Prefix tree或Digit tree，左圖是維基百科的實(shí)例，這是個(gè)典型的沒有任何優(yōu)化的前綴樹，一方面，只有單分叉的情況下也多分出一級(jí)，比如inn；另一方面，由于在分支節(jié)點(diǎn)需要分配 2 ^ s * pointer 的內(nèi)存，對(duì)于實(shí)際扇出極少的場景，內(nèi)存損耗非常大。

RadixTree是一種通過合并前綴（PathCompression）優(yōu)化內(nèi)存的前綴樹。合并前綴是指壓縮掉僅有一個(gè)孩子的分支節(jié)點(diǎn)，這樣存在的節(jié)點(diǎn)或者是葉子節(jié)點(diǎn)，或者是有分叉的分支節(jié)點(diǎn)。名字中的radix=2^span，它在radix=2的情況下，也叫做Patricia tree[6]。Linux PageCache頁面緩存用的是RadixTree，以太坊幣ETH的核心數(shù)據(jù)結(jié)構(gòu)是Merkle Patricia tree。中間圖是按照RadixTree重新組織的。

即便有合并前綴，由于大部分扇出是填不滿，浪費(fèi)了空間。比如上面例子的RadixTree(radix = 256, s=8)，那么即便在第一級(jí)只有t、A、i，也需要多分配 253 * 8 ~ 1Kbytes。調(diào)整radix(span = lg(radix))是一種內(nèi)存優(yōu)化方式，但這提高了樹高增加了緩存失效[5]。2013年，A(daptive)R(adix)T(ree)[6]用自適應(yīng)的節(jié)點(diǎn)類型來解決問題，用適合數(shù)據(jù)分布的最緊湊的節(jié)點(diǎn)表示，而不是固定的Node256。論文中 InnerNode 分為 Node4、Node16、Node80和Node256這四種，按照實(shí)際需要的分叉數(shù)選擇，通過類分?jǐn)偹惴?Amortization Alg)復(fù)雜度分析方法，可證明理論上這棵樹內(nèi)存復(fù)雜度是O(52N)，其中N是存儲(chǔ)數(shù)據(jù)量。ART論文提供了一種方式，在提高扇出降低樹高的同時(shí)，還能大幅度降低內(nèi)存開銷。按照ART重新組織上面例子中的RadixTree，如圖所示。

5、HIT優(yōu)化，RC實(shí)現(xiàn)ShortList+LongList Leaf的自適應(yīng)

我們定義 RC_x 為不超過x個(gè)元素的連續(xù)存儲(chǔ)空間，支持Append-Only和Mark-Delete操作，單元素額外成本不超過8byte。接下來看RC的設(shè)計(jì)要點(diǎn)。

既然RC被設(shè)計(jì)為只支持Append-Only/Mark-Delete修改的數(shù)據(jù)類型，為此元數(shù)據(jù)需有cursor和valids。同時(shí)針對(duì)不同容量的RC，為了控制理論上單條數(shù)據(jù)損耗不超過8byte，需要分別設(shè)計(jì)和實(shí)現(xiàn)，我們不希望引入繼承virtual指針的內(nèi)存開銷，采用根據(jù)type分發(fā)的實(shí)現(xiàn)方案。

RC1元數(shù)據(jù)8byte，可輕松容納cursor和valids，那么下一階的RC_x，x是幾呢？按照分?jǐn)偡治龇椒ǎ琑C_x至少有2個(gè)元素，也就是16byte的預(yù)算，在分配前還是要先看選型，RC_x需要變長因此元數(shù)據(jù)還有留出來8byte給dataptr，這樣的話，valids不能采用std::bitset<N>，因?yàn)閎itset的實(shí)現(xiàn)至少需要一個(gè)字也就是8byte。valids和cursor用bit field 的方式來做分配看上去還是比較充裕的，存放58個(gè)數(shù)據(jù)元素都沒問題，實(shí)際上考慮到系統(tǒng)分配器的特點(diǎn)，我們并沒有這樣做。

主流的系統(tǒng)分配器大部分是slab-based，在實(shí)際應(yīng)用時(shí)，除過理論單條數(shù)據(jù)損耗，還需要考慮因內(nèi)存池帶來的對(duì)齊損耗。一方面，RC1所在的鏈約占整體的80%，這樣海量的小對(duì)象適合用內(nèi)存池來管理，為避免檢索時(shí)候多一次內(nèi)存池地址轉(zhuǎn)化，我們把vaddr存儲(chǔ)在元數(shù)據(jù)中，釋放時(shí)再使用。另一方面，分散式地分配 N*sizeof(data)，會(huì)造成每類slab的內(nèi)部非充分使用，為此RC16+采取了Array of data_array的組織方式。

RC設(shè)計(jì)有不少實(shí)現(xiàn)細(xì)節(jié)，包括什么時(shí)候一次性多申請(qǐng)多少空間，控制內(nèi)存成本和操作效率。時(shí)間關(guān)系就不多介紹了。

6、LeafCompaction優(yōu)化稀疏

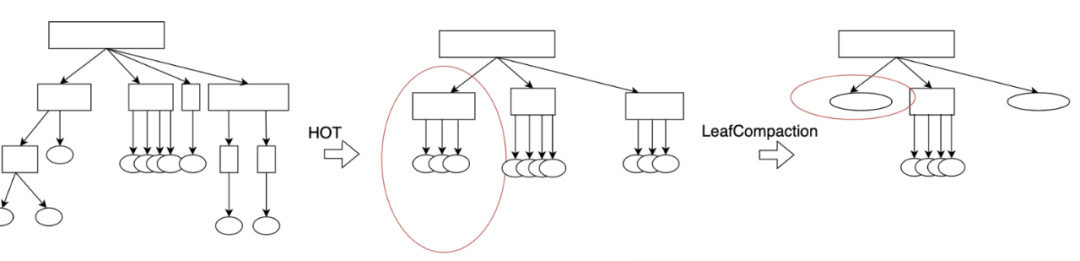
前綴樹在緩存失效方面優(yōu)于BTree，ART進(jìn)一步地采用自適應(yīng)節(jié)點(diǎn)類型，既能增加扇出優(yōu)化緩存訪問，又能控制內(nèi)存損耗。然而實(shí)際應(yīng)用中，ART仍然受到key值分布稀疏的影響，這表現(xiàn)為在部分子樹扇出很小很深（較Node256），樹高無法全面降低，從而影響點(diǎn)查的緩存。HOT[7]提出一種自適應(yīng)動(dòng)態(tài)span提升平均扇出，進(jìn)而降低樹高的方法，具體來說，定義節(jié)點(diǎn)最大扇出k，尋找一種樹的劃分，在每個(gè)劃分的分支節(jié)點(diǎn)數(shù)不大于k-1的前提下，沿著葉子到根的劃分?jǐn)?shù)的最大值取最小，這樣的實(shí)際效果就是對(duì)于稀疏段的span足夠大，對(duì)于密集段的span足夠小，整體扇出逼近最大扇出k。如中圖所示。

對(duì)于ART+目標(biāo)的連續(xù)性應(yīng)用場景來說，僅僅提升扇出降低樹高是不夠的，我們發(fā)現(xiàn)存在扇出很高，但扇出后葉子數(shù)據(jù)很稀疏，同時(shí)總數(shù)據(jù)量也不高，這顯然影響了掃描性能。我們提出葉子合并（LeafCompaction），它包括判定器和操作算法。給定一個(gè)分支節(jié)點(diǎn)，如果它被判定為合并，則用一個(gè)葉子節(jié)點(diǎn)替換它，該葉子節(jié)點(diǎn)的前綴同該樹的前綴，內(nèi)容是該樹的數(shù)據(jù)，后續(xù)插入/刪除過程遵從葉子的操作方式；如果它被判定為不變，則保持。給定一個(gè)葉子節(jié)點(diǎn)，如果它被判定為分裂，則用一顆樹替換它，該樹的前綴同該葉子的前綴，內(nèi)容通過BulkLoad的方式生成，如果它被判定為不變，則保持。判定器的默認(rèn)算法依據(jù)子樹平均和總數(shù)，節(jié)點(diǎn)壓縮率高達(dá)90%。如圖所示。

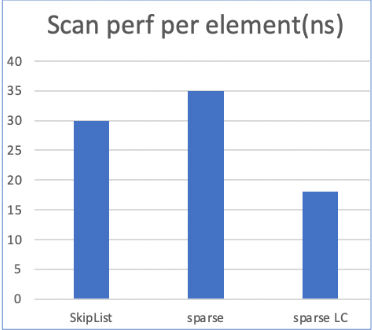
實(shí)際評(píng)測效果，平均到單條數(shù)據(jù)的掃描性能，稀疏場景下LC版本優(yōu)于普通版本一倍。

7、RCU面向讀者實(shí)現(xiàn)讀寫安全

一般使用深度優(yōu)化的細(xì)粒度鎖來保護(hù)倒排數(shù)據(jù)結(jié)構(gòu)的并行操作，但鎖競爭帶來的性能抖動(dòng)，完全抹殺了訪存優(yōu)化，我們必須探索出一種無鎖(lock-free)安全模式。提到無鎖lock-free，大家都覺得是CAS，其實(shí)一方面CAS不是銀彈，CAS常見的寫法是whileloop直到成功，如果有10個(gè)線程都在高速修改一個(gè)鏈表尾巴，這時(shí)候CAS只是說把陷入內(nèi)核省掉了，但是還是要不停地重做，這并不能完全釋放并行的能力，最好能從業(yè)務(wù)上打散。另一方面，CAS也有問題，多核下 CPU cache coherence protocol總線仲裁，導(dǎo)致破壞流水線。

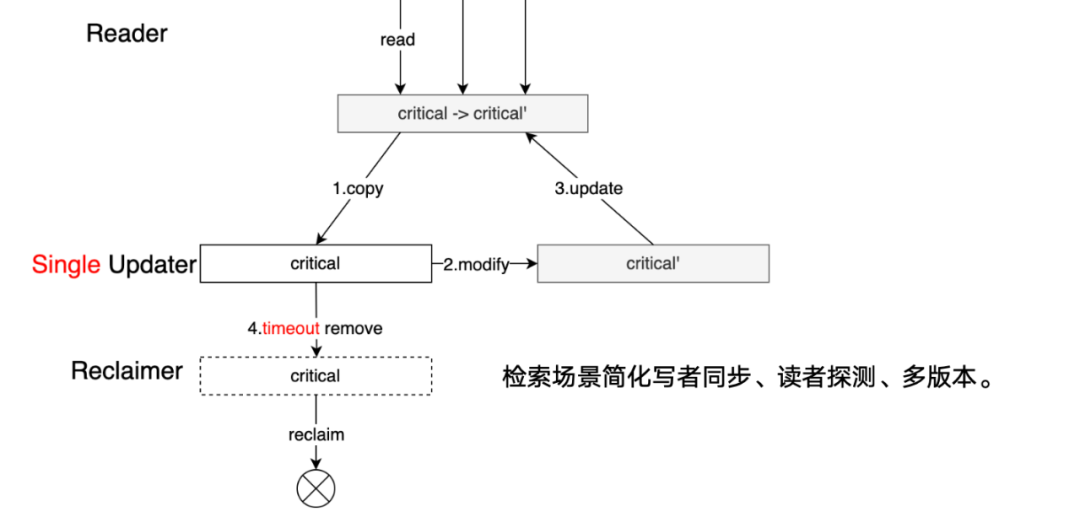
Read-Copy-Update 是Linux內(nèi)核中的一種同步機(jī)制，被用來降低讀者側(cè)的鎖開銷，同時(shí)提供安全的寫機(jī)制，具體地來說，多個(gè)讀者（reader）并行地訪問臨界資源，寫者（writer）在更新臨界資源（critical resource）時(shí)候，拷貝一份副本作為修改基礎(chǔ)，修改后原子性替換掉。當(dāng)所有讀者釋放了這個(gè)臨界資源后（Grace peroid），再釋放資源（reclaimer）。

Linux還需要較復(fù)雜的機(jī)制：

探測靜止?fàn)顟B(tài) Quiescent Status，當(dāng)所有CPU都經(jīng)歷過至少一次靜止?fàn)顟B(tài)時(shí)，才認(rèn)為Grace peroid結(jié)束；
多寫者間同步，避免丟失修改。

對(duì)于檢索服務(wù)來說，它有下面3個(gè)特點(diǎn)，這些特點(diǎn)大幅度地降低了我們的設(shè)計(jì)復(fù)雜度：

單寫者，我們可能有其他的準(zhǔn)備線程并行做更重的準(zhǔn)備工作，但只有Reload單線程負(fù)責(zé)物料更新；
非事務(wù)，檢索線程召回的多條數(shù)據(jù)間沒有嚴(yán)格約束；
讀者持有時(shí)間有限，檢索線程有嚴(yán)格的超時(shí)要求。這些特點(diǎn)大幅度地降低了我們的設(shè)計(jì)復(fù)雜度。

8、LearnedIndex面向Workload自適應(yīng)

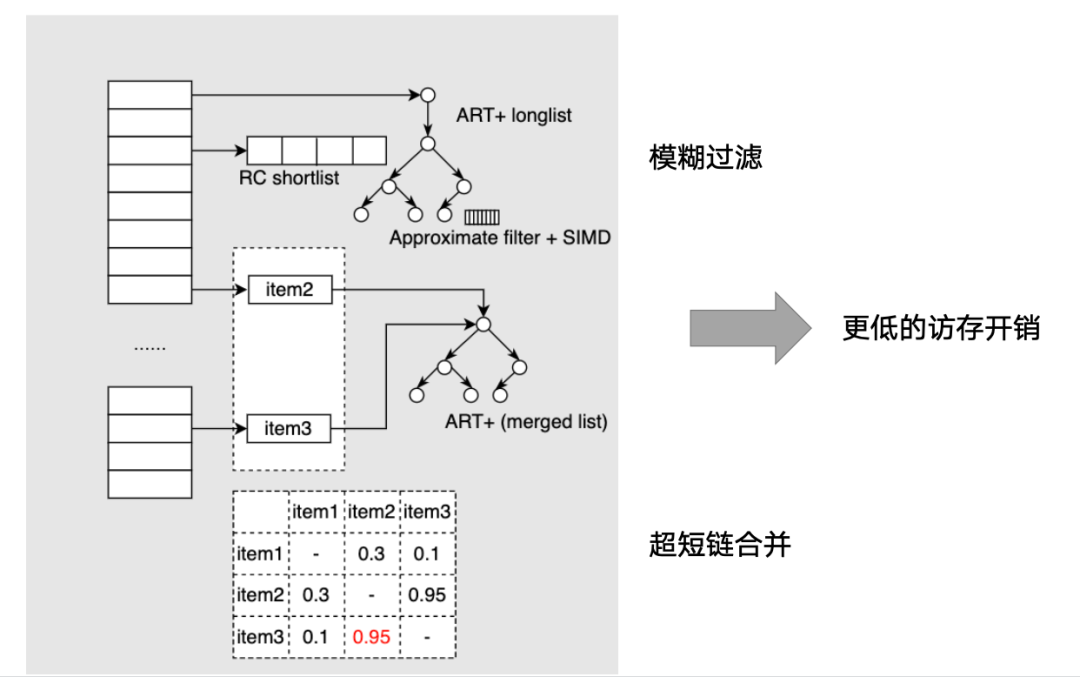
最后，我再介紹下進(jìn)行中的工作L2I。剛才都是對(duì)單鏈的優(yōu)化緩存失效，已有不錯(cuò)的效果，但從更宏觀全局的視角來看，我們系統(tǒng)還有可挖掘空間：一方面，廣告投放天然導(dǎo)致存在較多超短鏈，另一方面，需要掃描過程跨表查詢做各類過濾邏輯等等。這些已不單單是數(shù)據(jù)分布的問題，而是在線流量和客戶投放的匹配，需要用更智能的手段來解決。

行業(yè)里面，JeffDean&TimK 聯(lián)合發(fā)表了Learned Index[8]引入RMI、CDF的模型，后續(xù)TimK團(tuán)隊(duì)又有動(dòng)態(tài)化、多維索引、sagedb等多種方向的發(fā)展，本質(zhì)是構(gòu)建面向負(fù)載的半自動(dòng)化尋優(yōu)系統(tǒng)。我們既要引入負(fù)載特征，但由于掃描過程很輕量，不能做過重的預(yù)測，同時(shí)作為對(duì)客戶有承諾的商業(yè)系統(tǒng)，不能產(chǎn)生錯(cuò)誤。借鑒L2I的思想，我們還做了兩個(gè)事情，一方面、通過觸發(fā)出口離線計(jì)算共現(xiàn)關(guān)系，用來合并超短鏈、短鏈，用上HIT的高性能的連續(xù)掃描能力；另一方面，取熵最大的組合<pid,cid>，提取到倒排表的bit位，確定不過1，否則為0，對(duì)于后者 fallback到點(diǎn)查計(jì)算。