譯者 | 朱先忠
審校 | 孫淑娟

圖1:原作者自己設計的Iluminado項目的封面
2019年世界衛生組織估計,全球共有約22億視力障礙者,其中至少有10億人本可以預防或仍在治療。就眼部護理領域而言,全世界面臨許多挑戰,包括預防、治療和康復服務的覆蓋面和質量不平等。缺乏訓練有素的眼部護理人員,眼部護理服務與主要衛生系統的整合也很差。我的目標是激發人們的行動來共同應對這些挑戰。本文中展示的項目是我目前正在進行的數據科學頂峰項目Iluminado的一部分。
Capstone項目的設計目標
我創建本文項目的目的是想訓練一個深度學習集成模型,最終實現該模型對于低收入家庭來說非常容易獲得,并且可以以低成本執行初始疾病風險診斷。通過使用我的模型程序,眼科醫生就可以根據視網膜眼底攝影確定是否需要立即進行干預。
項目數據集來源
OphthAI提供了一個名為視網膜眼底多疾病圖像數據集(Retinal Fundus Multi-Disease Image Dataset,簡稱“RFMiD”)的公共可用圖像數據集,該數據集包含3200張眼底圖像,這些圖像由三臺不同的眼底相機拍攝,并由兩名資深視網膜專家根據已裁決的共識進行注釋。
這些圖像是從2009-2010年期間進行的數千次檢查中提取的,既選擇了一些高質量的圖像也包含不少低質量的圖像,從而使數據集更具挑戰性。
數據集共分為三個部分,包括訓練集(60%或1920張圖像)、評估集(20%或640張圖像)和測試集(20%和640張)。平均而言,訓練集、評估集和測試集中的患有疾病的占比分別為60±7%、20±7%和20±5%。該數據集的基本目的是解決日常臨床實踐中出現的各種眼部疾病,共確定了45類疾病/病理。這些標簽可以分別在三個CSV文件中找到,它們是RFMiD_Training_Labels.CSV、RFMiD_Validation_Labels.SSV和RFMiD_Testing_Labels.CSV。
圖像來源
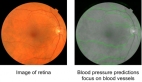
下面這張圖是用一種被稱為眼底照相機的工具拍攝的。眼底照相機是一種專門的低倍顯微鏡,連接在一臺閃光照相機上,用來拍攝眼底,即眼睛后部的視網膜層。
現在,大多數眼底照相機都是手持式的,因此患者只需直視鏡頭。其中,明亮的閃光部分表示已拍攝眼底圖。
手持攝像機是有其優點的,因為它們可以被攜帶到不同的位置,并且可以容納有特殊需求的患者,例如輪椅使用者。此外,任何接受過所需培訓的員工都可以操作攝像頭,從而能夠使服務水平低下的的糖尿病患者可以快速、安全、高效地進行年度檢查。
眼底視網膜成像系統拍照情況:
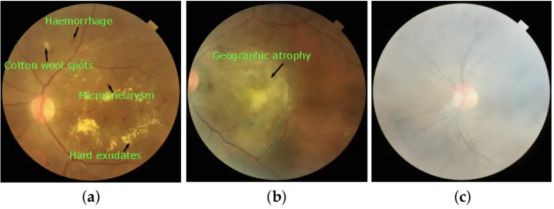
圖2:基于各自視覺特征拍攝的圖像:(a)糖尿病視網膜病變(DR)、(b)老年性黃斑變性(ARMD)和(c)中度霾(MH)。
最終診斷在哪里進行?
最初的篩查過程可以通過深度學習來輔助,但最終診斷由眼科醫生使用裂隙燈檢查進行。
這一過程也被稱為生物顯微鏡診斷,它涉及對活細胞的檢查。醫生可以進行顯微鏡檢查,以確定病人的眼睛是否出現任何異常。
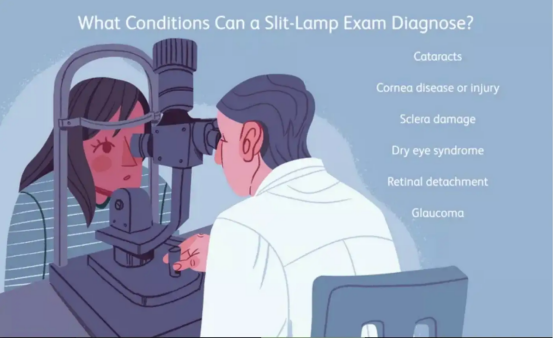
圖3:裂隙燈檢查圖示
深度學習在視網膜圖像分類中的應用
與傳統的機器學習算法不同,深度卷積神經網絡(CNN)可以使用多層模型的辦法實現從原始數據中自動提取和分類特征。
最近,學術界發表了大量文章,都是有關使用卷積神經網絡(CNN)來識別各種眼部疾病的,如糖尿病視網膜病變和結果異常(AUROC>0.9)的青光眼等。
數據指標
AUROC分數將ROC曲線匯總為一個數字,該數字描述了模型在同時處理多個閾值時的性能。值得注意的是,AUROC分數為1代表是一個完美的分數,而AUROC得分為0.5對應于隨機猜測。
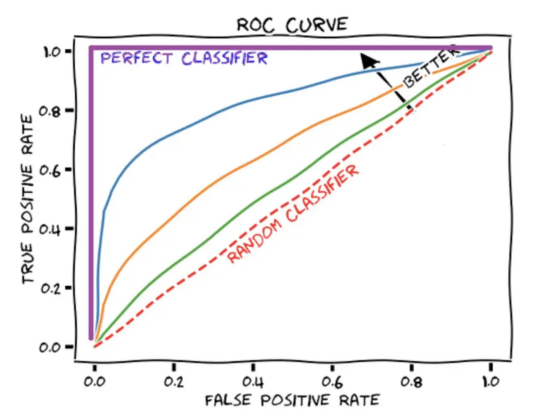
圖4:ROC曲線示意圖展示
所用方法——交叉熵損失函數
交叉熵通常在機器學習中用作損失函數。交叉熵是信息理論領域的一種度量,它建立在熵定義的基礎上,通常用于計算兩個概率分布之間的差異,而交叉熵可以被認為是計算兩個分布之間的總熵。
交叉熵也與邏輯損失有關,稱為對數損失。盡管這兩種度量方法來自不同的來源,但當用作分類模型的損失函數時,這兩種辦法計算的數量相同,可以互換使用。
(有關具體詳情,請參考:https://machinelearningmastery.com/logistic-regression-with-maximum-likelihood-estimation/)
什么是交叉熵?
交叉熵是給定隨機變量或事件集的兩個概率分布之間差異的度量。您可能還記得,信息量化了編碼和傳輸事件所需的位數。低概率事件往往包含更多的信息,而高概率事件則包含較少的信息。
在信息論中,我們喜歡描述事件的“驚訝”。事件發生的可能性越小,就越令人驚訝,這意味著它包含了更多的信息。
- 低概率事件(令人驚訝):更多信息。
- 高概率事件(不足為奇):信息較少。
在給定事件P(x)的概率的情況下,就可以為事件x計算信息h(x),如下所示:
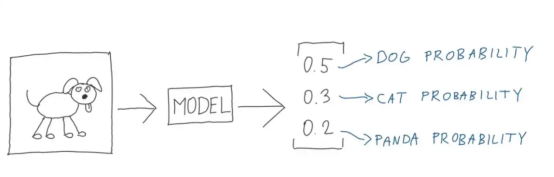
圖4:完美的插圖(圖片來源:Vlastimil Martinek)
熵是從概率分布中傳輸隨機選擇的事件所需的比特數。偏態分布具有較低的熵,而事件具有相等概率的分布一般具有較大的熵。
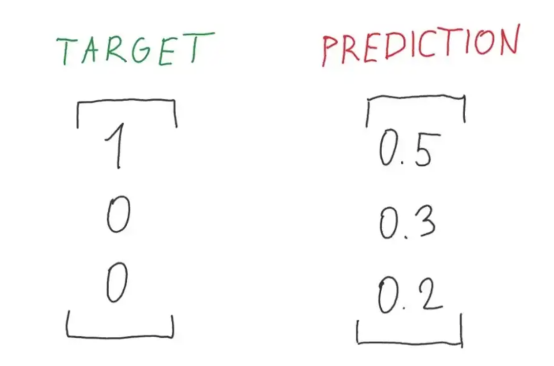
圖5:目標與預測概率之比的完美說明(圖片來源:Vlastimil Martinek)
偏態概率分布具有較少的“意外”,反過來也具有較低的熵,因為可能的事件占主導地位。相對來說,平衡分布更令人驚訝,而且熵更高,因為事件發生的可能性相同。
- 偏態概率分布(不足為奇):低熵。
- 平衡概率分布(令人驚訝):高熵。
熵H(x)可以針對具有x個離散狀態中的一組x的隨機變量及其概率P(x)計算,如下圖所示:
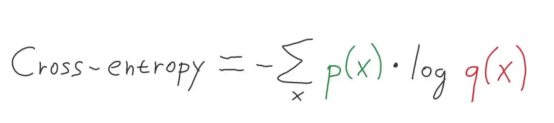
圖6:多級交叉熵公式(圖片來源:Vlastimil Martinek)
多類別分類——我們使用多分類交叉熵——屬于交叉熵的一種具體應用情形,其中的目標采用的是單熱編碼向量方案。(有興趣的讀者可參考Vlastimil Martinek的文章)

圖7:熊貓和貓損失計算的完美分解圖(圖片來源:Vlastimil Martinek)
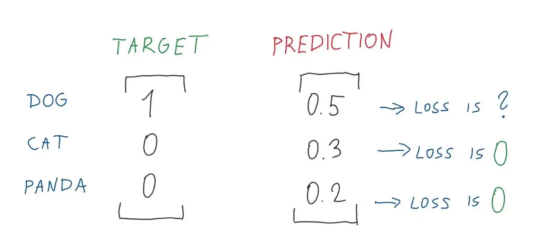
圖8:損失值的完美分解圖1(圖片來源:Vlastimil Martinek)
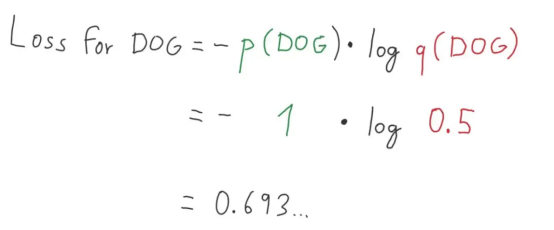
圖9:損失值的完美分解圖2(圖片來源:Vlastimil Martinek)
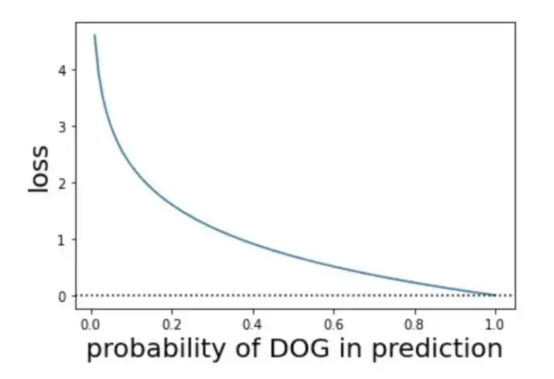
圖9:關于概率和損失的可視化展示(圖片來源:Vlastimil Martinek)
二元交叉熵怎么樣?

圖10:分類交叉熵公式圖解(圖片來源:Vlastimil Martinek)
在我們的項目中選擇使用了二元分類——二元交叉熵方案,即目標為0或1的交叉熵方案。如果我們將目標分別轉換為[0,1]或[1,0]的熱編碼向量方式并進行預測,那么我們就可以使用交叉熵公式來進行計算。

圖11:二元交叉熵計算公式圖解(圖片來源:Vlastimil Martinek)
使用非對稱損失算法處理不平衡數據
在一個典型的多標簽模型環境中,數據集的特征可能存在不成比例數量的正標簽和負標簽的情況。此時,數據集傾向于負標簽的這種趨勢對于優化過程具有主導性影響,并最終導致正標簽的梯度強調不足,從而降低預測結果的準確性。
這也正是我當前選用的數據集所面臨的情況。
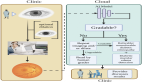
本文項目中采用了BenBaruch等人開發的非對稱損失算法(參考圖12),這是一種解決多標簽分類的方法,不過其中的類別也存在嚴重不平衡分布情形。
我想到的辦法是:通過不對稱地修改交叉熵中的正負分量,從而減少負標簽部分的權重,最終實現突出上述處理起來較為困難的正標簽部分的權重。
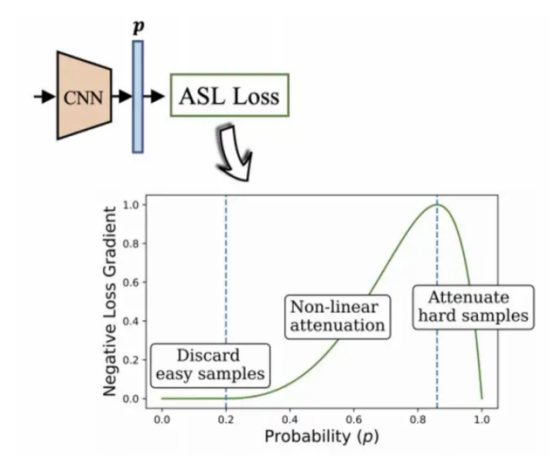
圖12:非對稱多標簽分類算法(2020,作者:Ben-Baruch等)
待測試的體系架構
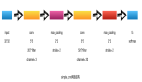
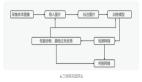
總體歸納一下,本文項目使用了如圖所示的體系架構:
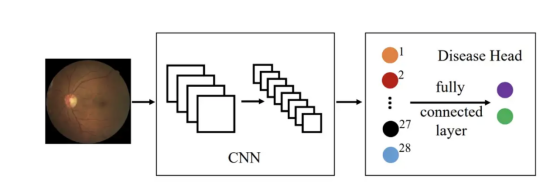
圖13(圖片來源:Sixu)
上述架構所采用的關鍵算法主要包括:
- DenseNet-121
- InceptionV3
- Xception
- MobileNetV2
- VGG16
另外,上述有關算法有關內容一定會在我完成本文Capstone項目后加以更新!有興趣的讀者敬請期待!
譯者介紹
朱先忠,51CTO社區編輯,51CTO專家博客、講師,濰坊一所高校計算機教師,自由編程界老兵一枚。
原文標題:??Deep Ensemble Learning for Retinal Image Classification (CNN)??,作者:Cathy Kam