TensorFlow Probability是一個(gè)構(gòu)建在TensorFlow之上的Python庫(kù)。它將我們的概率模型與現(xiàn)代硬件(例如GPU)上的深度學(xué)習(xí)結(jié)合起來(lái)。

極大似然估計(jì)

最大似然估計(jì)是深度學(xué)習(xí)模型中常用的訓(xùn)練過(guò)程。目標(biāo)是在給定一些數(shù)據(jù)的情況下，估計(jì)概率分布的參數(shù)。簡(jiǎn)單來(lái)說(shuō)，我們想要最大化我們?cè)谀硞€(gè)假設(shè)的統(tǒng)計(jì)模型下觀察到的數(shù)據(jù)的概率，即概率分布。

這里我們還引入了一些符號(hào)。連續(xù)隨機(jī)變量的概率密度函數(shù)大致表示樣本取某一特定值的概率。我們將表示這個(gè)函數(shù)??(??|??)，其中??是樣本的值，??是描述概率分布的參數(shù):

tfd.Normal(0, 1).prob(0)
 
 <tf.Tensor: shape=(), dtype=float32, numpy=0.3989423>

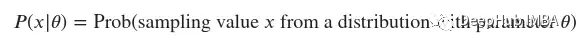
當(dāng)從同一個(gè)分布中獨(dú)立抽取多個(gè)樣本時(shí)(我們通常假設(shè))，樣本值??1，…，????的概率密度函數(shù)是每個(gè)個(gè)體????的概率密度函數(shù)的乘積:

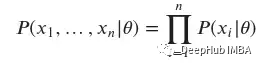
可以很容易地用一個(gè)例子來(lái)計(jì)算上面的問(wèn)題。假設(shè)我們有一個(gè)標(biāo)準(zhǔn)的高斯分布和一些樣本:??1=?0.5，??2=0和??3=1.5。正如我們上面定義的那樣，我只需要計(jì)算每個(gè)樣本的概率密度函數(shù)，并將輸出相乘。

X = [-0.5, 0, 1.5]
 
 np.prod(tfd.Normal(0, 1).prob(X))
 
 0.01819123

現(xiàn)在，我想直觀地告訴大家概率密度函數(shù)和似然函數(shù)之間的區(qū)別。它們本質(zhì)上是在計(jì)算類(lèi)似的東西，但角度相反。

從概率密度函數(shù)開(kāi)始，我們知道它們是樣本??1，…，????的函數(shù)。參數(shù)??被認(rèn)為是固定的。因此當(dāng)參數(shù)??已知時(shí)，我們使用概率密度函數(shù)，找出相同樣本??1，…，????的概率。簡(jiǎn)單地說(shuō)，當(dāng)我們知道產(chǎn)生某個(gè)過(guò)程的分布并且我們想從它中推斷可能的抽樣值時(shí)，我們使用這個(gè)函數(shù)。

對(duì)于似然函數(shù)，我們所知道的是樣本，即觀測(cè)數(shù)據(jù)??1，…，????。這意味著我們的自變量現(xiàn)在是??，因?yàn)槲覀儾恢朗悄膫€(gè)分布產(chǎn)生了我們觀察到的這個(gè)過(guò)程。所以當(dāng)我們知道某個(gè)過(guò)程的樣本時(shí)，使用這個(gè)函數(shù)，即我們收集了數(shù)據(jù)，但我們不知道最初是什么分布生成了該過(guò)程。也就是說(shuō)既然我們知道這些數(shù)據(jù)，我們就可以對(duì)它們來(lái)自的分布進(jìn)行推斷。

對(duì)于似然函數(shù)，慣例是使用字母??，而對(duì)于概率密度函數(shù)，我們引入了上面的符號(hào)。我們可以這樣寫(xiě):

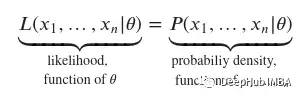
我們準(zhǔn)備定義參數(shù)為??和??的高斯分布的似然函數(shù):

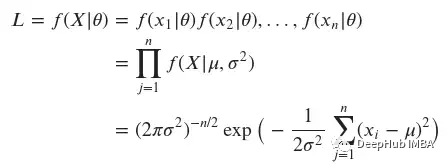
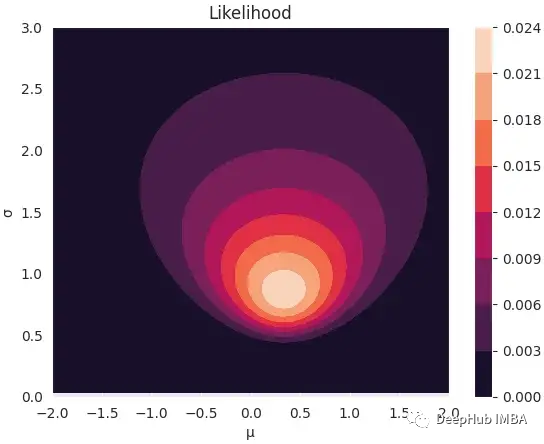
作為對(duì)似然函數(shù)有更多直觀了解，我們可以生成足夠多的樣本來(lái)直觀地了解它的形狀。我們對(duì)從概率分布中生成樣本不感興趣，我們感興趣的是生成參數(shù)??，使觀測(cè)數(shù)據(jù)的概率最大化，即??(??1，…，????|??)。

我們使用與上面相同的樣本??1=?0.5，??2=0和??3=1.5。

X
 
 [-0.5, 0, 1.5]

為了能夠構(gòu)建2D可視化，我們可以創(chuàng)建一個(gè)潛在參數(shù)的網(wǎng)格，在一段時(shí)間間隔內(nèi)均勻采樣，??從[-2,2]采樣，??從[0,3]采樣。由于我們對(duì)每個(gè)參數(shù)采樣了100個(gè)值，得到了??^2個(gè)可能的組合。對(duì)于每個(gè)參數(shù)的組合，我們需要計(jì)算每個(gè)樣本的概率并將它們相乘。

μ = np.linspace(-2, 2, 100)
 σ = np.linspace(0, 3, 100)
 
 l_x = []
 for mu in μ:
  
  
  
 l_x = np.asarray(l_x).reshape((100, 100)).T

現(xiàn)在準(zhǔn)備繪制似然函數(shù)。注意這是觀察到的樣本的函數(shù)，這些是固定的，參數(shù)是我們的自變量。

plt.contourf(μ, σ, l_x)
 plt.xlabel('μ')
 plt.ylabel('σ')
 plt.colorbar()
 plt.title('Likelihood');

我們感興趣的是最大化數(shù)據(jù)的概率。這意味著想要找到似然函數(shù)的最大值，這可以借助微積分來(lái)實(shí)現(xiàn)。函數(shù)的一階導(dǎo)數(shù)對(duì)參數(shù)的零點(diǎn)應(yīng)該足以幫助我們找到原函數(shù)的最大值。

但是，將許多小概率相乘在數(shù)值上是不穩(wěn)定的。為了克服這個(gè)問(wèn)題，可以使用同一函數(shù)的對(duì)數(shù)變換。自然對(duì)數(shù)是一個(gè)單調(diào)遞增的函數(shù)，這意味著如果x軸上的值增加，y軸上的值也會(huì)增加。這很重要，因?yàn)樗_保概率對(duì)數(shù)的最大值出現(xiàn)在與原始概率函數(shù)相同的點(diǎn)。它為我們做了另一件非常方便的事情，它將乘積轉(zhuǎn)化為和。

讓我們執(zhí)行變換:

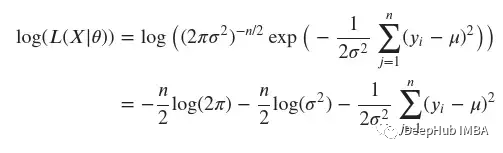
現(xiàn)在可以著手解決優(yōu)化問(wèn)題了。最大化我們數(shù)據(jù)的概率可以寫(xiě)成:

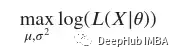
上面的表達(dá)式可以被求導(dǎo)以找到最大值。展開(kāi)參數(shù)有l(wèi)og(??(??|??，??))。由于它是兩個(gè)變量??和??的函數(shù)，使用偏導(dǎo)數(shù)來(lái)找到最大似然估計(jì)。

專(zhuān)注于??′("撇"表示它是一個(gè)估計(jì)值，即我們的輸出)，我們可以使用以下方法計(jì)算它:

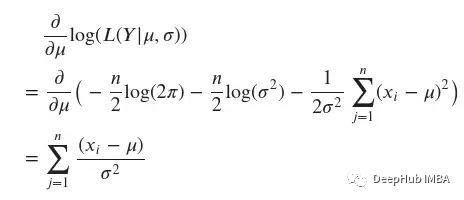
為了找到最大值，我們需要找到臨界值，因此需要將上面的表達(dá)式設(shè)為零。

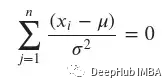
得到

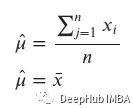
這是數(shù)據(jù)的平均值，可以為我們的樣本??1=?0.5，??2=0和??3=1.5計(jì)算μ和σ的最大值，并將它們與真實(shí)值進(jìn)行比較。

idx_μ_max = np.argmax(l_x, axis=1)[-1]
 print(f'μ True Value: {np.array(X).mean()}')
 print(f'μ Calculated Value: {μ[idx_μ_max]}')
 print(f'σ True Value: {np.array(X).std()}')
 print(f'σ Calculated Value: {σ[np.nanargmax(l_x[:,idx_μ_max], axis=0)]}')
 
 μ True Value: 0.3333333333333333
 μ Calculated Value: 0.3434343434343434
 σ True Value: 0.8498365855987975
 σ Calculated Value: 0.8484848484848485

最大似然估計(jì)在TensorFlow Probability中的實(shí)現(xiàn)

我們先創(chuàng)建一個(gè)正態(tài)分布隨機(jī)變量并從中取樣。通過(guò)繪制隨機(jī)變量的直方圖，可以看到分布的形狀。

x_train = np.random.normal(loc=1, scale=5, size=1000).astype('float32')[:, np.newaxis]
 
 plt.hist(x_train, bins=50);

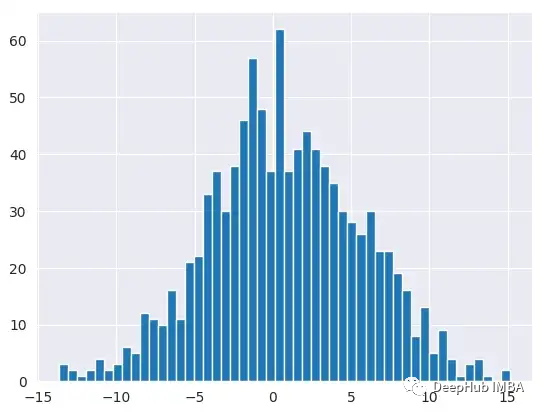
然后計(jì)算隨機(jī)變量的均值，這是我們想用最大似然估計(jì)學(xué)習(xí)的值。

x_train.mean()
 
 0.85486585

將TensorFlow Variable對(duì)象定義為分布的參數(shù)。這向TensorFlow說(shuō)明，我們想在學(xué)習(xí)過(guò)程中學(xué)習(xí)這些參數(shù)。

normal = tfd.Normal(loc=tf.Variable(0., name='loc'), scale=5)
 normal.trainable_variables
 
 (<tf.Variable 'loc:0' shape=() dtype=float32, numpy=0.0>,)

下一步是定義損失函數(shù)。我們已經(jīng)看到了我們想要達(dá)到的目標(biāo)最大化似然函數(shù)的對(duì)數(shù)變換。但是在深度學(xué)習(xí)中，通常需要最小化損失函數(shù)，所以直接將似然函數(shù)的符號(hào)改為負(fù)。

 def nll(x_train):
    return -tf.reduce_sum(normal.log_prob(x_train))

最后建立訓(xùn)練程序，使用自定義訓(xùn)練循環(huán)，可以自己定義過(guò)程細(xì)節(jié)(即使用自定義損失函數(shù))。

使用tf.GradientTape()，它是訪問(wèn)TensorFlow的自動(dòng)微分特性的API。然后指定要訓(xùn)練的變量，最小化損失函數(shù)并應(yīng)用梯度。

 @tf.function
 def get_loss_and_grads(x_train):
    with tf.GradientTape() as tape:
        tape.watch(normal.trainable_variables)
        loss = nll(x_train)
        grads = tape.gradient(loss, normal.trainable_variables)
    return loss, grads
 
 optimizer = tf.keras.optimizers.SGD(learning_rate=0.001)

現(xiàn)在訓(xùn)練程序已經(jīng)準(zhǔn)備完畢了。

 @tf.function
 def get_loss_and_grads(x_train):
    with tf.GradientTape() as tape:
        tape.watch(normal.trainable_variables)
        loss = nll(x_train)
        grads = tape.gradient(loss, normal.trainable_variables)
    return loss, grads
 
 optimizer = tf.keras.optimizers.SGD(learning_rate=0.001)
 
 Step 000: Loss: 13768.004 Loc: 0.855
 Step 001: Loss: 13768.004 Loc: 0.855
 Step 002: Loss: 13768.004 Loc: 0.855
 ...
 Step 1997: Loss: 13768.004 Loc: 0.855
 Step 1998: Loss: 13768.004 Loc: 0.855
 Step 1999: Loss: 13768.004 Loc: 0.855

我們通過(guò)最大化在第一時(shí)間生成的抽樣數(shù)據(jù)的概率，計(jì)算了參數(shù)??的最大似然估計(jì)。它是有效的，因?yàn)槟軌虻玫揭粋€(gè)非常接近原始值的??值。

 print(f'True Value: {x_train.mean()}')
 print(f'Estimated Value: {normal.trainable_variables[0].numpy()}')
 
 True Value: 0.8548658490180969
 Estimated Value: 0.8548658490180969

總結(jié)

本文介紹了最大似然估計(jì)的過(guò)程，和TensorFlow Probability的實(shí)現(xiàn)。通過(guò)一個(gè)簡(jiǎn)單的例子，我們對(duì)似然函數(shù)的形狀有了一些直觀的認(rèn)識(shí)。最后通過(guò)定義一個(gè)TensorFlow變量、一個(gè)負(fù)對(duì)數(shù)似然函數(shù)并應(yīng)用梯度，實(shí)現(xiàn)了一個(gè)使用TensorFlow Probability的自定義訓(xùn)練過(guò)程。