概念及入門
前言
在數據領域,有幾類經典的查詢場景:
- 想要統計某段時間內訪問某網站的 UV 數,或是統計某段時間內既訪問了頁面 A 又訪問了頁面 B 的 UV 數,亦或是統計某段時間內訪問了頁面 A 但未訪問頁面 B 的 UV 數,通常我們對這種查詢叫做基數統計。
- 想要觀察某些指標的數據分布,例如統計某段時間范圍內訪問頁面 A 與頁面 B 各自的瀏覽時長 95 分位數、50 分位數,則需要用到分位數統計。
- 想要統計某段時間內播放量最多或者點擊率最高的 10 個視頻或者文章(熱榜列表),則需要用到 TopN 統計。
這幾類問題在數據量不大的情況下都是非常容易處理的。我們可以通過遍歷+排序輕易而準確的解決這種問題。但一旦數據到達 Billion 量級,常規算法可能要花費數小時甚至數天的時間,并且即使提供充足的計算資源也于事無補,因為這幾類問題都難以并行化處理。
DataSketches[1] 就是為了解決大數據和實時場景下的這幾類典型問題而誕生的一組算法,最初由雅虎開源。這些算法以犧牲查詢結果的精確性為代價,可以在極小的空間內并行、快速地解決上述幾類問題。
Sketch 結構的核心思想
Sketch 結構即「數據草圖」結構,主要是為了計算海量的流式數據的概率指標而設計的一種數據結構。一般占用固定大小的內存,不隨著數據量的增加而增大。這種結構通過巧妙地保存或丟棄一些數據的策略,將數據流的信息抽象存儲起來,匯總成 Sketch 結構,最終能根據 Sketch 結構還原始數據的分布,實現基數統計、分位數計算等操作。
Sketch、Summary 都可以理解為數據草圖,不同論文中使用的稱呼不太一致,但是符號一般都是大寫的 S。
Sketch 一般具有以下幾個特征:
1. 單次遍歷
可以把 Sketch 理解為一個狀態存儲器,它時刻承載著數據流迄今為止的所有歷史信息,因此 Sketch 通常是 single-pass 的,只需要遍歷一遍數據即可取得所需的統計信息。
2. 占用空間小
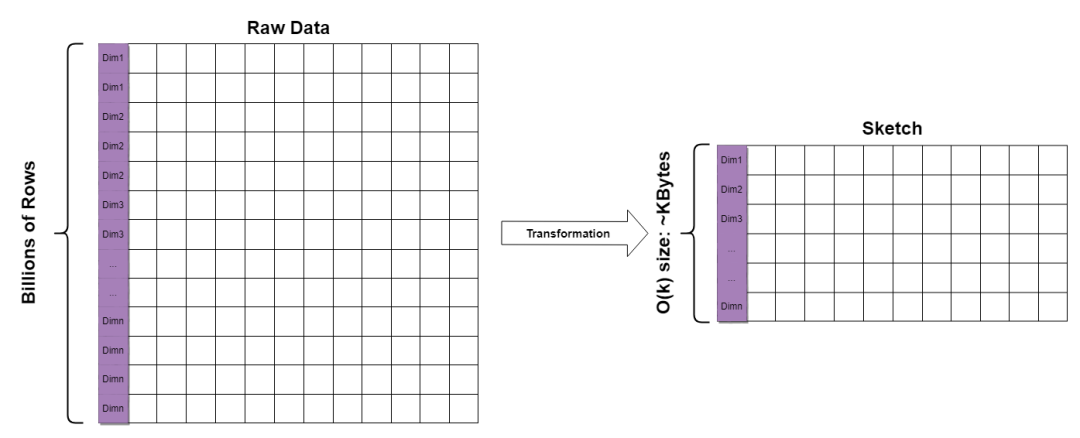
傳統的統計方式需要維護一個巨大的數據列表,且隨著數據的輸入越來越大。Sketch 可以在很小的常量空間內攝入海量的數據,通常在 KB 量級。這使得 Sketch 在海量數據的統計中非常有優勢。
對于一個包含上億條數據、包含多個維度組合的數據集,可以在每個維度組合上轉化生成一個 KB 大小的 Sketch 結構,從而加快查詢。
3. 可合并性
可合并性使得 Sketch 可以自由地分布式并行處理大量數據,因此具有快速、高效的優勢。以基數統計 (Distinct Value, DV)為例,要解決的問題是從具有重復元素的數據流中查找不同元素的數量,Sketch 可以輕易地將局部統計結果合并為全局統計結果,而直接計數則做不到這一點,即:
- DV(uid | city=北京 or 上海) ≠ DV(uid | city=北京) + DV(uid | city=上海)
- Sketch(uid | city=北京 or 上海) = Sketch(uid | city=北京) + Sketch(uid | city=上海)
PS: 第二個式子中的加號代表 Sketch 的合并操作。
在分布式計算中,兩個處在不同機器的 Sketch 的局部統計結果可以直接通過一個 Query 方法合并成一個 Sketch 結構,進行最終的分位數查詢。

4. 誤差可控的近似值
Sketch 為了節省空間必然會丟失一部分信息,因此統計結果不可能是完全精確的。但在現實中,許多分析和決策也并不要求數據是絕對精確的,有時候知道某個統計數據在 1% 的誤差范圍內往往跟精確的答案一樣有效。Sketch 可以在計算復雜度與誤差之間進行權衡,足以滿足大數據場景下大部分的統計需求。
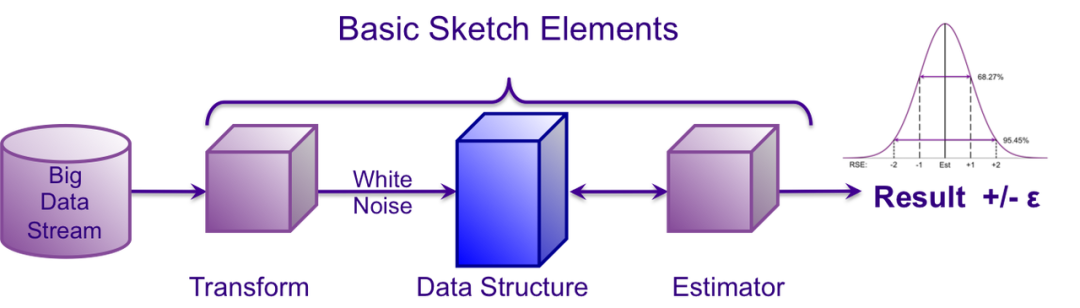
一個 Sketch 算法的使用流程通常如下:
原始數據經過轉化生成一個 Sketch 結構,當要進行查詢的時候,從 Sketch 生成一個 Estimator 返回查詢結果
Quantile 的定義
分位點/分位數(Quantile):考慮誤差近似,即給定誤差 ε 和分位點 φ,只需要給定排序區間[(φ - ε)*N, (φ + ε)*N] 內的任意元素即可(N 為元素個數)。
舉個例子,如果給定 input 序列如下,在 ε= 0.1 的情況下,求 PCT50(即 φ = 0.5)。返回 24、39、51 都是可以滿足條件的。但如果 ε= 0.01,只有返回 39 才是正確的結果。
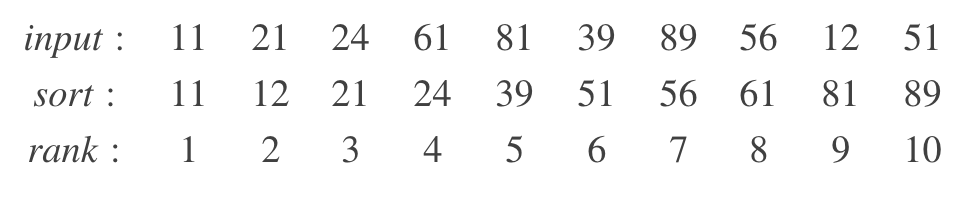
φ= 0.5 and ε = 0.1
Rank = [4, 5, 6] → V = [24, 39, 51]
這也就是為什么我們使用 DoublesSketch UDF 或者 Spark 的分位數近似算法的時候可能會出現分位數計算結果不準確的問題。此外,不同的分位數定位方法也會導致數據有細微的差距,后面會提及。
圖中,在當前維度下的數據只有兩條,針對這兩條數據求 50 分位數的結果會不一樣。在小基數求分位數問題的時候,數據會出現較大的誤差。
Quantile 的誤差
quantile 和 rank 實際上是兩個函數:
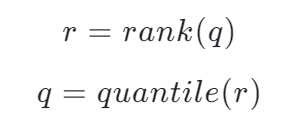
我們期待一對完美的函數,使得 q = quantile(rank(q)) 或者 r = rank(quantile(r)),但現實中,我們往往只能得到兩個有誤差的函數 r' = rank(q)和 q' = quantile(r)
分位數問題其實就是 quantile(r)問題,即給定 r,根據估計出來的 quantile 函數求出 q'。
函數的誤差由多種途徑帶來:
- 海量數據必然導致我們需要對數據進行有條件的整合和過濾,由此引入誤差。但合理的整合、過濾機制能夠將誤差控制在一定范圍內。為此,無數 researcher 貢獻了各種 idea,這也是文檔后半部分介紹的主要內容。
- 重復值也會帶來誤差。但實際上,如果我們對分位點的定義和邊界條件做了正確的假設,那么這種誤差已經被考慮在了算法之內,本文不再做詳細解釋。舉一個簡單的例子給大家感受一下,不同分位數定位方法與重復值是如何帶來誤差的:
Example
有五個數據輸入進來計算分位點:{10, 20, 20, 20, 30}
上邊是原始數據經過排序后的數值和位置對應圖,下邊則可以想象成一個簡單的存儲了這些數據的 Sketch 結構。
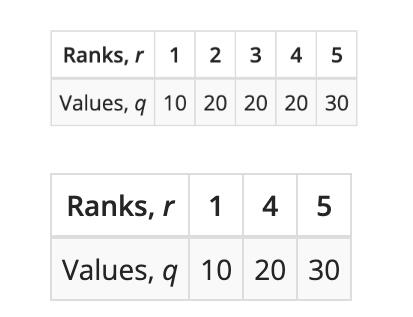
在計算分位點的時候有兩種定位分位點的規則,LT (less-than) 和 LE (less-than or equals)。兩者在舉例中有區別,但是上升到泛化問題上則區別不大,都屬于可接受誤差范圍內,在這個例子中我們對比 LT 和 LE 規則下得到的結果,能發現在重復值 20 上的 Rank' 和 Quantile' 是不一樣的,并且在邊界上的值的 Rank' 和 Quantile' 也有誤差。
LT (less-than) & GT(greater-than)

LE (less-than or equals) & GE(greater-than-or-equal)

想了解 LT 和 LE 規則的區別可以瀏覽 DataSketches 官網里關于 Quantiles 的定義[2]
業界 Quantile 實現
Quantile Sketches 經過層層迭代和不斷的演進,已經形成多種變種。以 Apache DataSketches 中的實現總結[3]為例,很多 Sketches 算法早已應用在了諸如 Spark、Hive、Druid 等等大數據開發常用框架中,當我們在 SQL 中調用 percentile 類函數的時候,不同框架會調用其對應的算法。但由于不同框架實現的算法不一樣,實現的效率也有高低,最終會導致在使用的時候能明顯感知到計算速度的差異。

KLL 和 GK 算法應該是目前被應用最廣泛的算法。這里,我們選取兩個大數據開發場景下最常用的兩個框架 Spark 和 Hive 來舉例,對比其中的分位數計算函數 percentile_approx 與一個由 Apache DataSketches 提供的算法實現,并簡單講解一下如何將 Apache DataSketches 提供的更高效的算法引入日常開發工作中。
Spark
在 Spark 中計算分位數不需要引入 UDF,Spark 中的 ApproximatePercentile[4] 類實現了 GK 算法,以 QuantileSummaries[5] 的結構作為數據 Sketch,后面會提到 GK 算法并且簡單解釋其概念。這個函數在數據量小的時候的計算效率是比較快的。
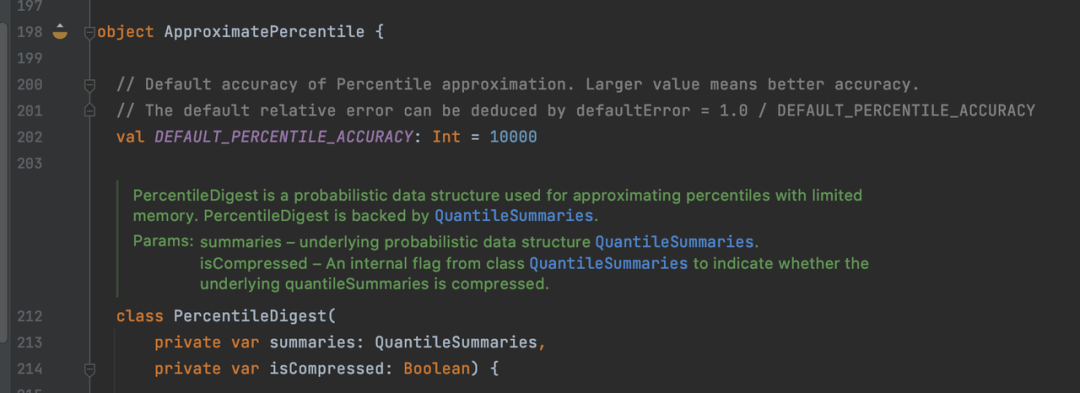
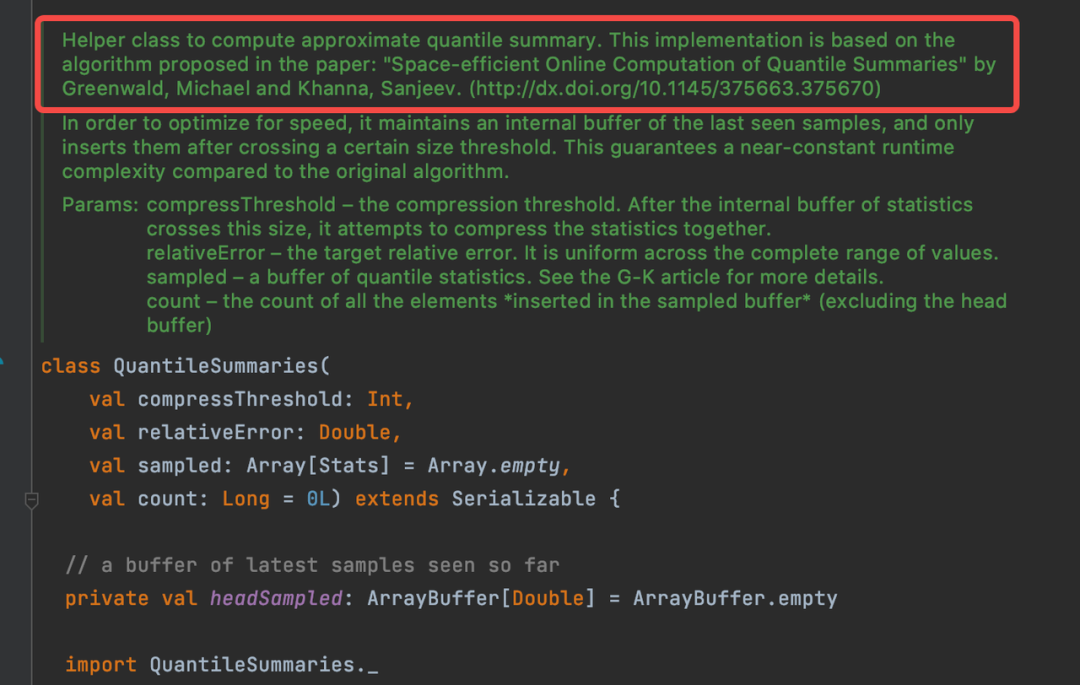
Hive
同樣,在 Hive 中計算分位數可以直接使用原生的分位數計算方法,但該方法背后算法并沒有 Spark 中的算法效率高效。Hive 中的 GenericUDAFPercentileApprox[6] 是通過計算近似數據直方圖的方式估算分位數。如 Hive 源碼提示,這個函數在數據量巨大的時候可能存在 OOM 的問題。此外,Hive 實現估計直方圖的算法主要依據 A Streaming Parallel Decision Tree Algorithm[7]。值得一提的是,這個算法的核心想法是如何在有限的內存中構建數據的直方圖。
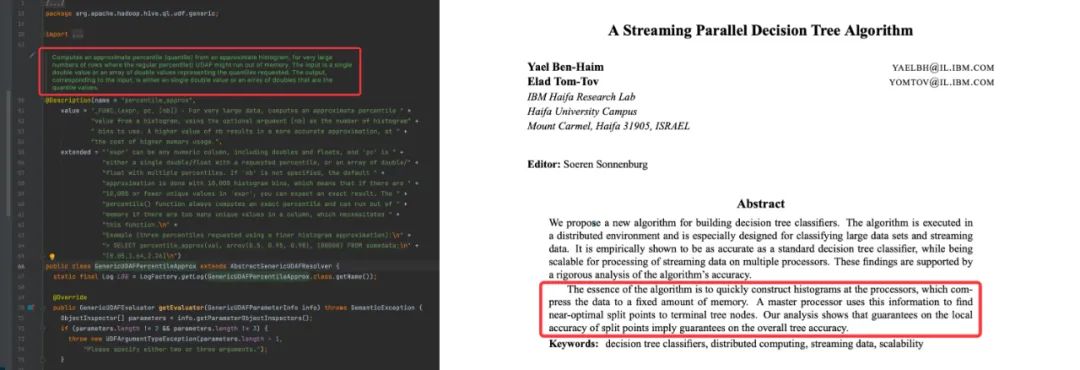
DataSketches
如果在面對海量數據的時候,Spark 原生分位數計算函數會顯得乏力,這時候就推薦引入 DataSketches 提供的分位數計算方法。該算法不光在空間占用上更優,其計算效率也更高。DataSketches 的 DoubleSketch[8] 是根據 Mergeable Summaries[9] 中提到的 Low Discrepancy Mergeable Quantiles Sketch 算法實現的。這篇論文主要討論了什么是 Mergeability 并對之前著名的算法的 Mergeability 進行了證明。同時提出了一個結合抽樣的 Randomized Mergeable Quantiles Sketch 算法。
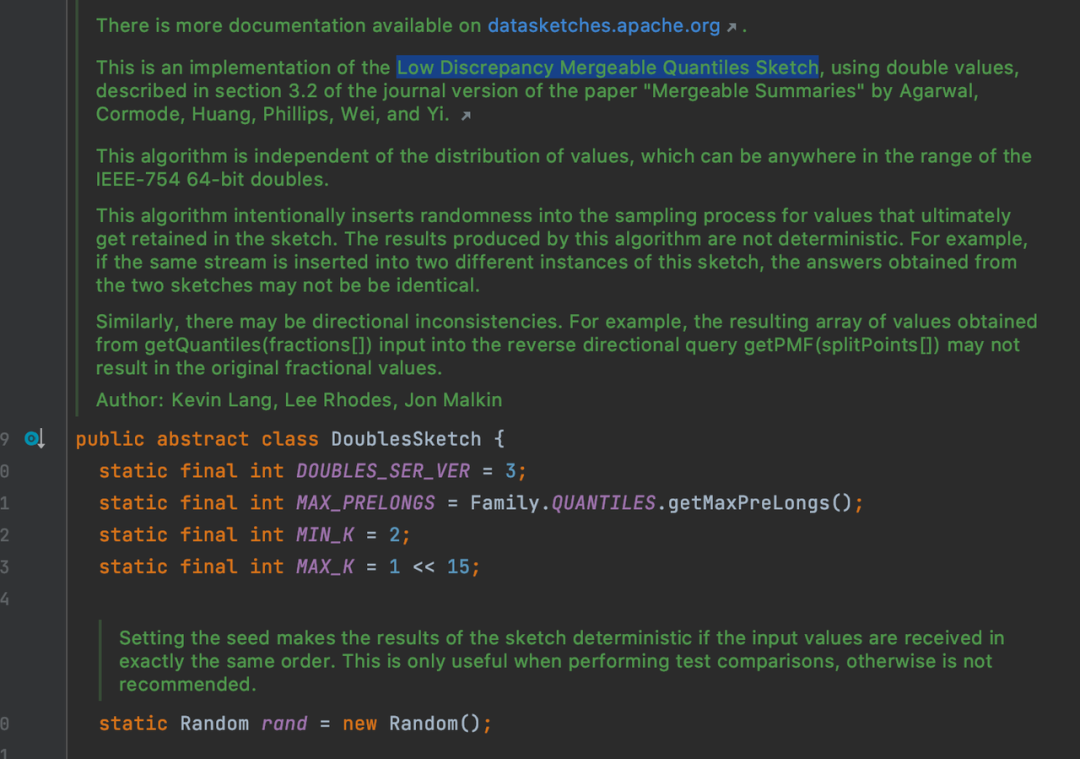
作為大數據開發同學,對于該算法需要了解以下幾點:
- 這個算法的 Sketch 結構能夠分布式進行。
- 由于算法引入隨機,每次的結果可能不同(但可以通過指定隨機種子來固定)。
- 算法實現上通過壓縮、位圖等操作進一步節省時空開銷。
- 能用這個算法就用這個算法,快得很!
算法落地到日常開發也很容易,Datasketches 已經提供了多種 UDF、UDAF,基本能夠滿足常見業務需求。需要先在 pom 文件中加入 org.apache.datasketches 依賴,然后可以根據業務需求,對 datasketches 提供的 UDF、UDAF 再次封裝。打包成 jar 包并注冊 UDF 之后,就可以在 SQL 中使用了。
Quantile Sketches 算法的演進過程
問題定義
Quantile Sketches 算法最早可以追溯到上世紀 90 年代,當流式數據以及分布式計算的概念剛剛在學術界得到普遍的認可,這個問題被拋了出來。如何在海量數據中,甚至無限數據中,使用有限的空間,找到其中的某一個 rank 對應的值,或找到某一個數對應的 rank。
Quantile Sketches 算法的發展依據重要的算法的推出,形成了幾個重要的階段。實際上,這個領域的初心是如何使用最小的內存空間,解決一個最泛化的問題。

什么是最泛化的問題呢?學術界把這種問題稱為 All Quantiles Approximation Problem,其定義如下:

與最泛化問題相對應,狹義問題被稱為 Single Quantile Approximation Problem。當然還有很多問題的變體,例如,給定 rank 求對應的數值(最常見的分位數問題)或者已知流數據大小求解 rank 或分位數等。
在明確了問題定義后,同樣也需要明確對算法的定義,一個合格的 Quantile Estimators 應該具備以下四種特性:
- 提供可調節的、可以被明確的誤差區間。
- 與輸入數據獨立。
- 只遍歷一次所有數據。
- 應使用盡可能小的內存。
合格的 Estimator 并沒有對可合并性作出什么顯性的要求,mergeability 只是一個 nice to have 的特性。問題定義中并沒有考慮 mergeability 的問題,所以有些算法沒有實現 mergeability,導致無法完全適配實際生產中的分布式計算模式。即使適配,往往也需要更多空間,更高的計算復雜度。
空間優化的終點在哪里?
業界和學術對于探索未知的東西往往具有相同的方法論:先找到最小內存占用的天花板在哪里。通過構造特殊的對抗數據流并且證明了在極端情況下,任何算法都需要的最小的內存。如何找到這個問題的天花板并不是本文的重點,感興趣的讀者可以閱讀論文 An Ω (1/ε log 1/ε) Space Lower Bound for Finding ε-Approximate Quantiles in a Data Stream[10] 進一步了解。
從壓縮出發 - MRL 算法[11]
最簡單的壓縮
數據丟棄
回想之前講解基礎概念的時候提及的例子,我們可以直觀的感受到,Sketch 數據結構的一個特性就是對數據進行合理的壓縮。壓縮后的數據盡可能的能夠全面還原數據原本的分布。為了實現這一原理,最直觀的想法就是針對每一個輸入數據通過某種規則選擇丟棄或保留,并確保將誤差控制在 ε 以內。那么問題就變成了如何找到合適的丟棄規則。
舉個例子,可以根據數據的 index 來判斷是否丟棄:對于一個未排序的數據流,丟棄所有偶數位的數字,而保留奇數位的數字。但這顯然是一個有缺陷的方法,而且很容易證明:只需要構建一個數據流,將所有較小的數據都放在偶數位,那么留下的數據則都是較大的數據,其中最小的數據也會大于或等于中位數。
從這個例子中得到啟發,我們可以先對數據流進行排序,然后再根據上面的原則來丟棄數據,那么這個方法就變得可行了。
權重增加
另一個顯而易見的邏輯是,丟棄的數據不能單純地丟棄,它的信息必須以某種方式保存在未丟棄的數據中。繼續上例,偶數位置的數據被丟棄,可以同時增大它前一個奇數位置數據的權重,使得一個奇數位數字表示原本一個奇數位+偶數位的數字。這樣,數據量的信息就保存了下來,權重越大,也就意味著在這個區域內的數據越多。
Batch 思想
然而流數據并不支持實時排序,并且隨著數據規模增大,排序所需要的時間和空間開銷都會不斷增長。一個自然的想法是,可以把流數據劃分成一個個的 batch,在每一個 batch 內部排序。
下圖中的例子結合了數據丟棄和權重增加兩個策略。其中,第一行是輸入數據被切分成一個個小 batch 并經過內部排序后的樣子。第二行表示丟棄所有偶數位的數據,并增加前一位奇數位數據的權重(小方格的高度增大了一倍)。第三行表示丟棄所有奇數位的數據,并增加后一位偶數位數據的權重。可以觀察到,一些位置的 Rank 發生改變,如果 Compactor 內部數據是偶數的時候 Rank 不發生改變,如果是奇數則會相對加一或減一。按照這個過程就可以構建一個最簡單的 Sketch 結構。
單個 batch 數據壓縮問題的思路得到了初步的驗證,那么問題來了,單個 batch 如何推演到多個 batch 甚至流數據上的呢?
壓縮與合并
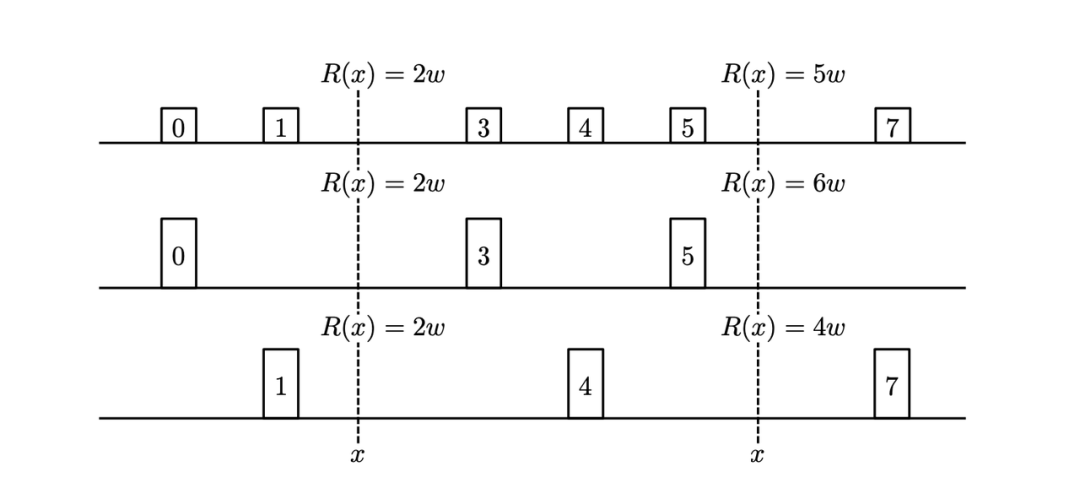
假設有兩個 Sketch 結構,我們想要達成的效果是,當把這兩個 Sketch 結構合并成一個之后,仍然能夠提供準確的 Rank。
如下圖所示,紅點表示數據 s_i < v,當我們把兩個 Sketch 結構合并后發現,v 在合并后的數據集中的 Rank 就等于兩個 Sketch 分別統計紅點個數的和,合并數據集的 Rank 不會因為拆分統計而變化。
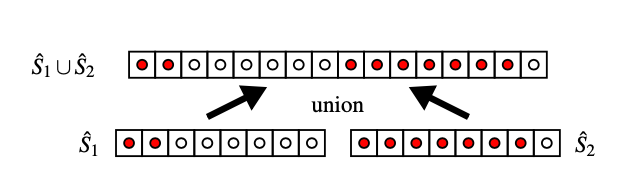
因此,我們得到兩條推論:
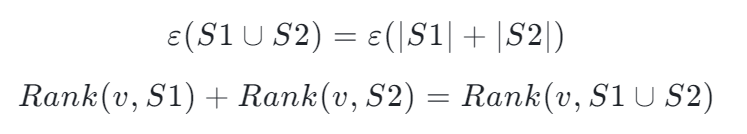
但如果單純地把兩組數據拼接在一起,顯然會面臨數據量增加帶來的空間開銷增大的問題。此時再回到之前提到的壓縮、合并的思路,可以將這個過程不斷循環起來,即合并、壓縮、再合并、再壓縮……
MRL 算法原理簡介
Random Sampling Techniques for Space Efficient Online Computation of Order Statistics of Large Datasets[11](MRL 算法)就是在壓縮、合并思想上加以改進得來的。MRL 算法構建了一個樹狀多層級壓縮合并結構:
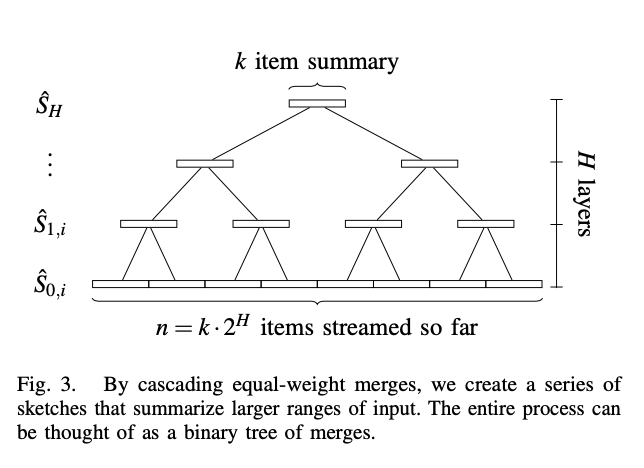
選擇一個固定大小的 k 作為 Sketch 結構的大小。根據流數據量大小可以反推需要壓縮的層級數 H。顯然,k 越大壓縮層級越少,相對丟失的信息就越少,結果就越精確。
過程很簡單,原始流數據輸出到 level0 的一個 Sketch 結構中,當數據填滿了大小為 k 的 Sketch 結構后,如果 level0 沒有其他 Sketch,則這個 Sketch 暫時緩存下來,等待另一個 Sketch 到來。如果有另一個 Sketch,則將兩個 Sketch 歸并排序后保留所有奇數位置的數據,將 2k 大小的數據壓縮為 k 大小并傳入下一層級。同樣,如果下一層級已經存在一個 Sketch,那么進行類似的歸并排序和丟棄壓縮后,將 Sketch 傳入下一層級,層層遞進。
k 的大小直接影響數據準確性,甚至還決定了這個算法能否收斂,比較合適的取值為 k = O(ε^{?1} _ log^2(εn))。MRL 算法在每一層級只需要兩個 Sketch 結構存儲數據。層級數決定了所需要的總共空間大小,而層級數的是根據總數據量和單個 Sketch 結構大小推演得到的:
O(H) = O(log^2(n/k)) = O(log^2(εn)), 總共空間 O(kH) = O(ε^{-1} _ log^2(εn))。
從抽樣出發 - Sample 算法[12]
假如現有一億個數字,我們想要對其中的某一個數字 x 求他的 Rank 是多少,Reservoir-Based Random Sampling with Replacement from Data Stream[12] 告訴我們,通過隨機抽樣我們可以用下面的公式從樣本估計整體的 Rank:
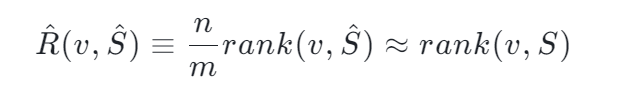
但這個是一個近似公式。一個嚴謹的算法需要搞清楚,這東西有多近似。碰巧存在這么一個不等式 Hoeffding's inequality 并根據 Hoeffding's inequality 推出了這么一個定理
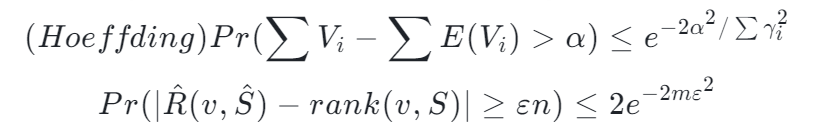
作為使用方,能理解證明是最好的,所以指路這篇文章的 VI 部分[13]。但是如果不理解證明,那么下面這段話會告訴你這個證明干了什么,有什么重要的意義(個人理解,可能存在不準確的地方,歡迎指正)。
本質上,Hoeffding's inequality 給出了隨機變量的和與其期望值偏差的概率上限。這個不等式是一個 Bernoulli 過程的一個衍生(關于 Hoeffding's inequality 更詳細的指路這里[14])。這種隨機抽樣到估計一個數字的 Rank 也是存在聯系的(誤差上限)。這種上限恰巧能夠讓把估計誤差限定在一個范圍內,滿足了 Quantile Sketch 算法的要求。況且抽樣的過程將 Rank 結果與數據量 n 獨立開來。結果的誤差只取決于 m。而 m 是我們可以設定的一個數,換句話說,m 是我們可以設定的一個內存大小,這個內存大小決定了抽樣后估計的 Rank 的誤差上限。
可以觀察到,這里所需要的內存大于 MRL 算法。但是它的最大意義在于移除了與數據量大小 n 的關系。需要明確的是,這種抽樣需要預先知道數據量大小 n,如果不知道數據量大小 n,抽樣仍然是有用的,但需要隨著數據量增大而降低抽樣概率。詳情見[13]
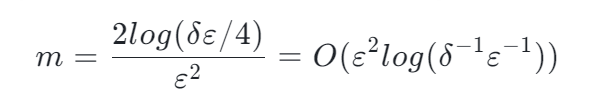
從結構出發 - GK 算法[15]
Summary 結構設計
GK 算法 Space-Efficient Online Computation of Quantile Summaries[15] 的靈感來源于下面這個想法:假設我們收到的流數據的第一個數字就是中位數,那么我們只需要隨著數據的輸入統計大于這個數的數量和小于這個數的數量,最后就能很輕易的驗證這個數是不是中位數。我們能不能對 k 個輸入的數據都保持這個一個結構,記錄大于這個結構的數據的個數和小于這個結構的數據的個數,那能找到對應數字的 Rank 是多少了。
存在下面一個結構,每一個 tuple 存儲真實值、最小 Rank、最大 Rank,每一個 tuple 叫 Summary:
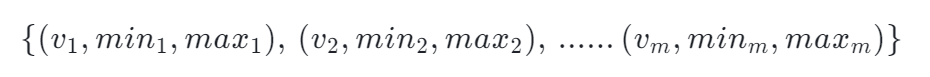
對于任意數據,只要滿足下面的公式,那么算法總體誤差就是收斂的。
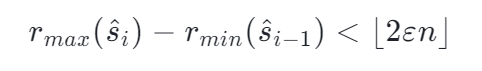
但是這個結構存在缺陷。在處理流數據的時候,如果新來的數據需要插入中間,那么每次都需要更新后面所有的 Summary。這樣更新的復雜度實在太高了。GK 算法就此提出了一個針對插入數據操作更友好的 Summary 結構:
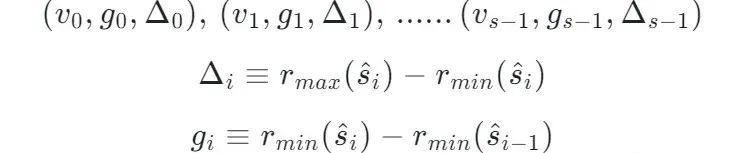
將絕對位置轉化成相對位置進行表示。
- g 表示兩個相鄰 Summary 的相對位置差異,根據 g 和一個起始點我們能夠推演出這個起始點和 Summary 的距離是多少。
- Δ 表示這個 Summary 覆蓋的 Rank 的范圍是多少。
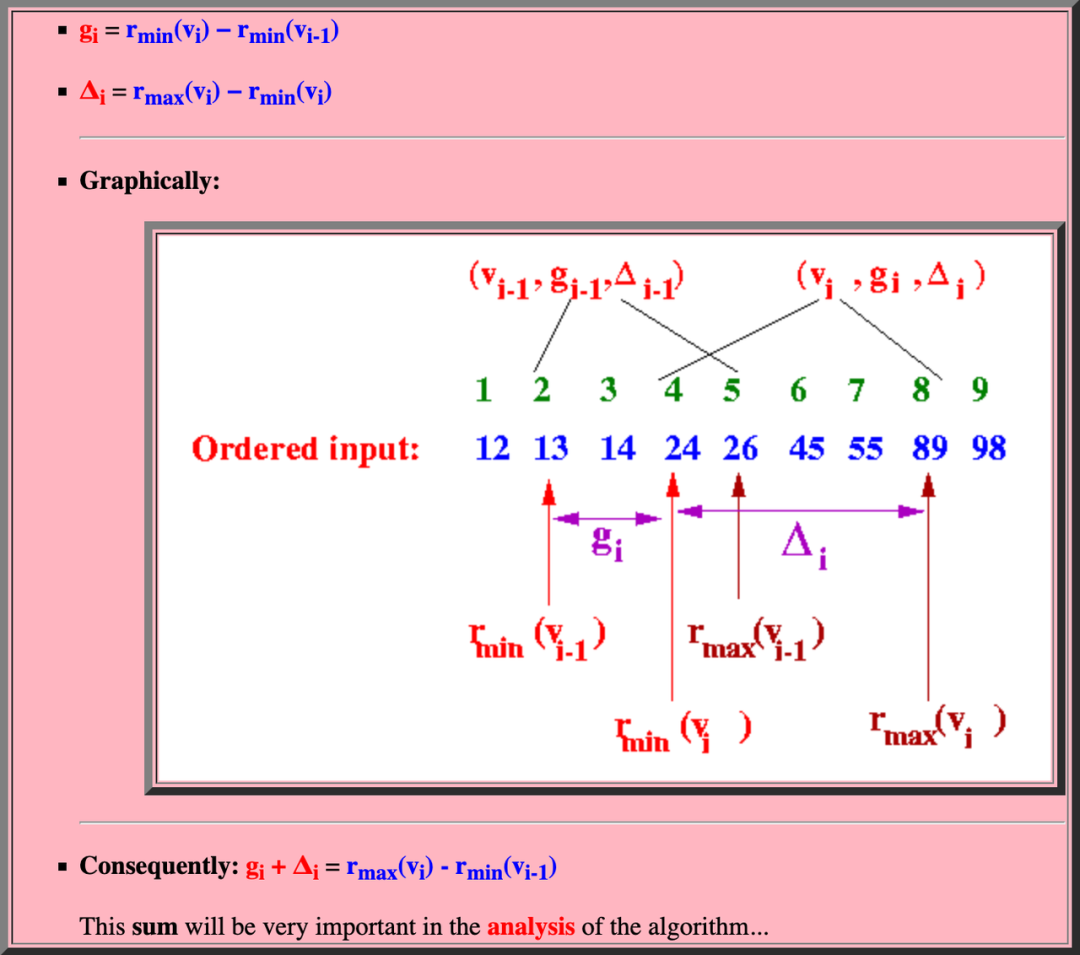
根據這個上面這個定義能推論出一下三條性質,詳細的推論這里不再贅述,有興趣的可以看這篇文章[16][17]

結合 Summary 結構的一些操作
經過一番數據公式的狂轟濫炸后,好像又摸不著 GK 算法在干什么了。如果想了解 GK 算法的細節,指路原始論文[15]。但如果僅僅想了解算法的思想,那么上面這都不重要,下面這段話告訴你這么一圈折騰到底為了什么。
如同數據庫的增刪改查一樣,構建這么一個特殊的 Summary 結構并推到這么多性質,只是為了更快、更方便的實行以下這些操作:
- 構建一個 Summary + 一個特殊的 INSERT() 方法 -> 使得更新數據特別快。
- 構建一個 Summary + 一個特殊的 QUERY() 方法 -> 使得查詢滿足誤差約束。
- 構建一個 Summary + 一個特殊的 DELETE() 方法 + 一個特殊的 COMPRESS() 方法 -> 使得空間保持不變且最優。
INSERT

最大最小情況都很好理解。對于一般情況,新插入的數據 i 顯然對 i-1 前面的任何數據都沒有影響,但是后面的數據每一個 Rank 都應該增加一位 ,所以 g = 1。精妙之處就在于用相對位置的變化累加而表示了絕對位置的變化。Δ = g_i + Δ_i - 1 的原因后文會提及。
QUERY
All Quantiles Approximation Problem 有一條必須要滿足的性質就是所有 x 都應該滿足|R'(x) ? R(x)| ≤ εn,白話文解釋就是,當我們發起一個查詢的時候(查詢 x 對應的 Rank)返回值的誤差都應該保持在一個與數據量成正比的線性關系中。
巧妙的設置查詢的方式就能將總體誤差控制在收斂范圍內。


DELETE and COMPRESSDELETE and COMPRESS
面對海量的數據,單純的增加信息而不對信息做壓縮刪減顯然是不合理的。刪除規則如下:

刪除操作只改變 v_i+1 所在 Summary 的 g_i+1, 并不改變 Δ_i+1。也就是說 Δ 越小,在滿足誤差約束下,具有合并更多 Summary 的潛力。
為了更加高效的對數據進行壓縮 GK 算法又提出了 Fullness、Capacity 和 Bands 三個概念。

這三個概念的誕生就是為了輔助進行 COMPRESS 操作的,簡單講,每個 Summary 對應的 Capacity 大小,從右向左來看,大小稱指數級倍數增大 ,而壓縮也是從右向左進行的。下圖展示了不同大小 Sketch 對應的每一個小的 Summary 的 Capacity 大小的關系,

下面的偽代碼展示了一個壓縮過程。滿足壓縮條件時,對 Summary 結構從右向左進行合并,使得 Summary 先嘗試最少的內存方法。

滿足壓縮條件后,相鄰 Summary 經過 COMPRESS 操作后,數據更新到 Band 值較小的 Summary 上。由于 DELETE 操作并不改變 Δ 的特性,如果保留 Band 值大的 Summary 結構,便有了更大的 Capacity,后期也就能夠容納更多的 Summary(將更多的 Summary 壓縮到一起)。
此外,GK 算法還引入了樹模型,通過右先序遍歷二叉樹,實現對于子節點的快速有序 COMPRESS 到父節點操作,不過,這里不再詳細介紹,感興趣的同學可以指路原始論文[15]。
需要注意的是,GK 算法是一個 mergeable 的算法,準確來說,是一個 One-way mergeable 的算法。
One-way mergeability is a weaker form of mergeability that informally states that the following setting can work: The data is partitioned among several machine, each creates a Summary of its own data, and a single process merges all of the summaries into a single one. 換句話說,One-way mergeability merge 算法不能夠分布式進行,否則誤差不在可控范圍內,而 Fully mergeable 的算法可以,雖然論文中對這點描述的不是特別清楚,但是詳細證明指路這幾篇講解 [18][19][20]。
GK 到底好在哪?
說了這么多 GK 算法的原理,這算法到底好在哪里?
- GK 算法以一種獨特的方式存儲了數據信息,實現了海量數據的高效查詢,高效插入。
- GK 算法在原本的樹狀模型上引入了不同層級則不同大小的 Summary 結構,更高效的利用了空間。
融合之開端 - ACHPWY 算法[9]
中國古話常講,取其精華,去其糟粕。后面的算法切實貫徹了這種思想。ACHPWY 算法 Mergeable Summaries[9] 的 Low Discrepancy Mergeable Quantiles Sketch 是一個基于 MRL 算法的衍生算法。在 MRL 算法上又增加隨機抽樣的方式,使得最終得到的 Quantile Estimator 是一個無偏的 Estimator。ACHPWY 算法的整體架構和 MRL 算法一樣,都采用相同的大小為 k 的 Sketch 結構,組成多層級樹狀模型。唯一不同的是,在進行 Sketch 合并的時候,引入隨機變量 F 來決定取奇數位置數據還是偶數位置數據。

原本 MRL 算法在任何合并時只取奇數位,隨機的引入帶來了 unbiased Estimator,并且帶來更少的空間使用空間的。如同上文解釋的一樣,如果需要探討隨機變量的和與其期望值偏差的概率上限,那么 Hoeffding's inequality 一定不會缺席的。具體的證明和講解請參考[9][13]。
而對空間使用大小的估計和 MRL 算法原理一樣,都是需要選擇一個合適的 k 作為 Sketch 結構的大小以達到空間最優的目的。總共需要的內存大小在 MRL 算法基礎上更進一步。

此外,相較于其他算法,ACHPWY 算法更加清楚的定義并證明了 One-way mergeability 在其算法的可行性。并且證明了 Same-weight merges 情況和 Uneven-weight merges 情況下的的可行性(誤差收斂),使得分布式的 merge 操作實現有了基礎。
融合之大鍋燉 - KLL 算法[21]
KLL 算法原理簡介
KLL 算法 Optimal Quantile Approximation in Streams[21] 可以理解為融合了之前提及的所有算法的優點,在空間上做出了極致的壓縮,并且全面的證明了 KLL 算法能解決 All Quantiles Approximation Problem。
根據以往經驗可知:
- 多層級的樹狀模型能滿足空間要求并且解決 All Quantiles Approximation Problem(MRL 算法)。
- 對數據流的隨機抽樣策略解耦了誤差與數據量大小的關系,但是單獨使用空間效率不如 MRL 算法高(Sample 算法)。
- 相對距離表示的數據結構 + 不同層級不同 Sketch 大小的策略提高了空間利用率(GK 算法)。
- 融合多層級樹狀壓縮模型 + 隨機抽樣的策略能夠產生 unbiased Estimator 并且帶來更高效的空間利用率(ACHPWY 算法)。
KLL 算法則把這四點融合起來,并加以改進,形成了這個更優的算法。
下圖展示了 KLL 算法融合迭代的過程:
- 第一層為使用空間指數級增大的 Sketch 結構的算法。
- 第二層將部分低層級的 Sketch 替換為 Sampler 的結構。
- 第三層將頂層 Sketch 結構替換為等大小的 Sketch 結構并使用 MRL 算法的思想。
- 第四層再次將頂層 Sketch 結構替換成等大小的 Sketch 結構并使用 GK 算法的思想。
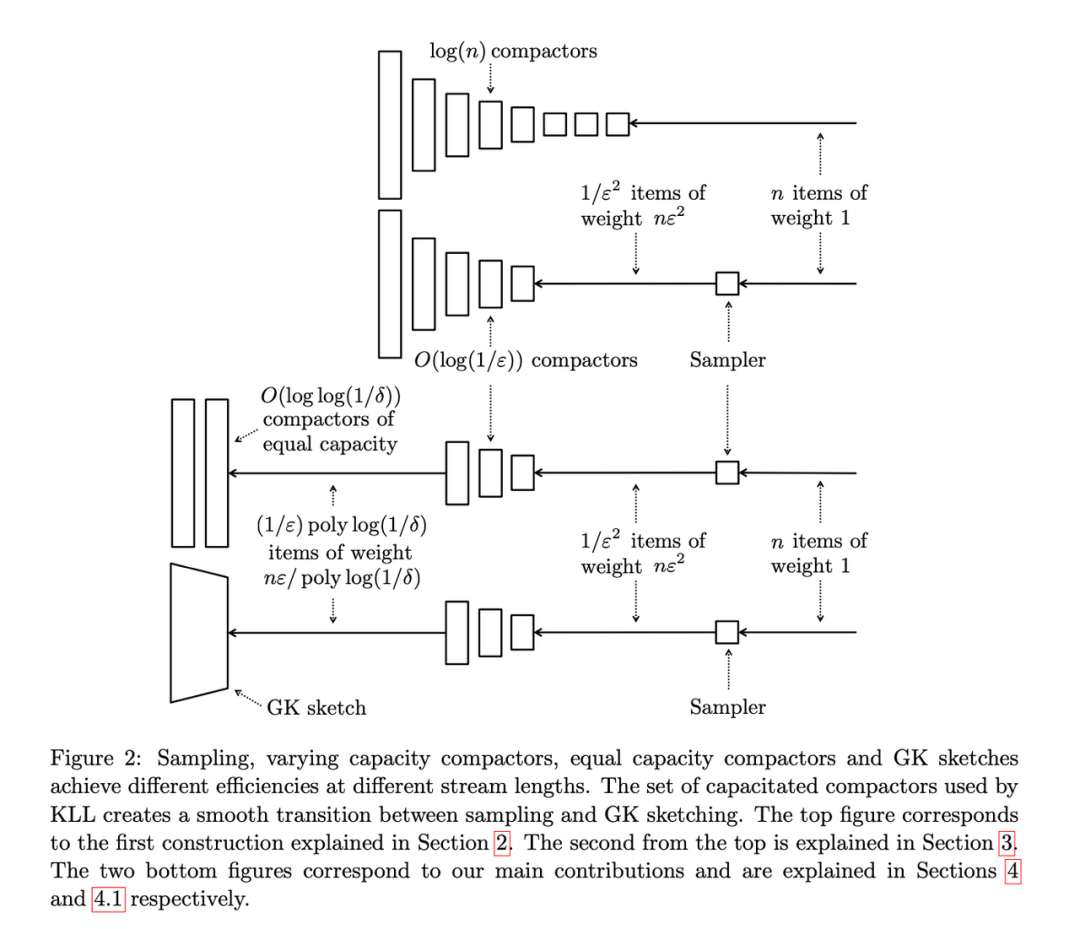
Sketch 空間指數增加設計
首先,為了節約空間,KLL 算法在 ACHPWY 算法基礎上將多層級同樣大小的壓縮結構轉化為指數級增大的壓縮結構。原理很好理解,數據剛輸入的時候沒有經過過多的壓縮,沒有帶來更多的誤差,自然需要更大的空間去限制誤差的增大。但隨著數據不斷壓縮合并,丟失的信息越來越多,自然需要更大的空間去限制誤差增大的趨勢。
Bernoulli Sampler
隨著層級的降低,低層級的 Sketch 結構空間大小不斷減小逐漸趨近于最小空間 2。如果空間小于 2,那么 Sketch 結構沒有辦法進行正常的壓縮。如果空間等于 1,Sketch 結構將變成一個沒有意義的數據傳輸通道。那為何不把這些等于 2 的 Sketch 結構換成一個簡單的 Bernoulli Sampler 呢?這樣能夠在解耦合數據量大小的時候還將 Quantile Estimator 轉化成一個 unbiased Estimator,還能更進一步節省空間。空間大小將不再與數據量大小有任何關系(即是這個空間大小大約之前提到的算法的最優解)。這種方法的所需空間大小為:
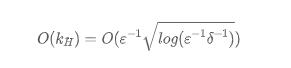
要想理解為什么這個結構能夠將所需空間和數據大小獨立開來,需要想象這么一個過程。隨著新的數據不斷的流入,在原本的最高層級 H 被裝滿后,自然會壓縮合并出下一個更高層級 H+1。那么假設 H+1-> H,我們知道,為了保證誤差的收斂,對于 Sketch 大小是根據下面這個公式算出來的。不難發現,當新的一個層級取代舊層級后,每一層級的 Capacity 其實都縮小了 1/c 倍。直到這個層級大小小于 2 的時候,Sketch 結構便轉化成一個 Bernoulli Sampler。將過小的 Sketch 結構 吸收到 Sampler 結構里使得整體的空間大小保持不變,是這個結構的核心優勢。
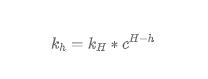
上層空間的進一步優化
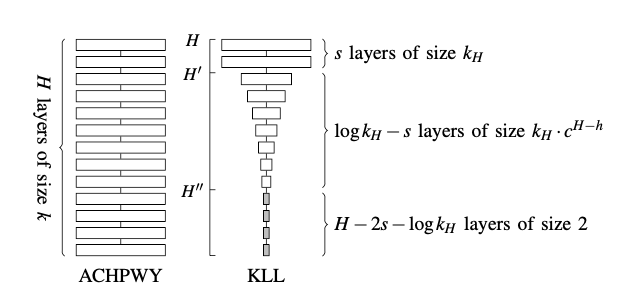
在此基礎上,KLL 另一個核心發現是,大量的誤差主要由最上面的幾層 Sketch 結構導致。優化最上面幾層的結構將大大降低誤差。KLL 算法提出將最上層的 s 個 Sketch 從指數大小關系轉化成固定大小關系(新的 Sketch 的空間大小不一定等于最高一層 Sketch 的空間大小),換句話說,將最上層的 s 個 Sketch 用 MRL 算法來實現。這種方法的所需空間大小為:
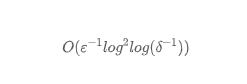
追求極致
為了追求極致的空間要求。KLL 算法提出用 GK 算法取代用 MRL 算法來實現最上層的 s 個 Sketch,因為理論上 GK 算法的所需空間更加的小。KLL 算法提出,將上層 s 個 MRL Sketch 拆分成兩個緊密相連的 GK Sketch,使得在任何合并的時候,都會至少有一個 GK Sketch 有數,并給出證明這種大融合的結構能夠達到的最優空間為:
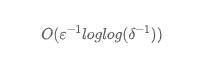
但是不得不提及的是 KLL 算法作者們沒有給出 Fully mergeable 的證明,也無法保證 Fully mergeable 的存在。因為 GK 算法只支持 One-way mergeable,本身就不是 Fully mergeable 的。所以業界實現的時候,通常選用上層為 MRL Sketch 的方法實現。
總結
到這里,這篇文章從 Sketch 結構的定義和特性出發,解釋了 Sketch 結構如何解決大數據計算場景中海量數據計算痛點,明確了 Quantile 問題的定義。其次,結合大數據開發中常用組件,討論了如何將 Quantile Sketch 算法帶入工程實踐中。本文著重介紹了 Quantile Sketches 算法原理,涵蓋了算法發展的幾個重要階段和重要產物。筆者嘗試用最簡單的語言和邏輯講解了每一個算法的核心思想、優點和缺陷,嘗試將多種算法的發展串聯起來,方便沒有相關背景的人從零開始了解這個領域。但實際上 Quantile Sketches 算法仍然有很多的變種,例如為解決長尾分布而優化的 Quantile Sketches 算法,為計算精確 PCT 邊界值而設計的 Digest 類算法[22][23],根據 Histogram 估計分位數的 Sketches 算法等……
希望大數據開發同學能夠了解算法推論、證明、衍生,期待有朝一日能看到以你們名字命名的 Quantile Sketches 算法。