用深度學習解決旅行推銷員問題,研究者走到哪一步了?

組合優化問題的背景
組合優化是數學和計算機科學交叉領域的一個實用領域,旨在解決 NP 難的約束優化問題。NP 難問題的挑戰性在于詳盡地尋找 NP 難問題的解超出了現代計算機的限制,因此不可能在大規模問題上最優地解決 NP 難問題。
我們為什么要關心這個問題?因為針對流行問題的穩健可靠的近似算法具有巨大的實際應用價值,并且也是現代產業的支柱。例如,旅行推銷員問題 (TSP) 是最流行的組合優化問題 (COP),從物流和調度到基因組學和系統生物學等多種應用中都有出現。
旅行推銷員問題是如此著名,或者說難以攻克,甚至有專門的 xkcd 漫畫!

TSP 和路由問題
TSP 也是路由問題的經典示例——路由問題是一類 COP,它需要一系列節點(例如城市)或邊(例如城市之間的道路)以特定順序遍歷,同時需要滿足一組約束或優化一組變量。TSP 要求按照確保所有節點都被訪問一次的順序遍歷一組邊。從算法的角度來看,我們的銷售人員的最佳「旅行」路線是一系列選定的邊,這些邊滿足了哈密頓循環中的最小距離或時間,請參見圖 1 中的說明。
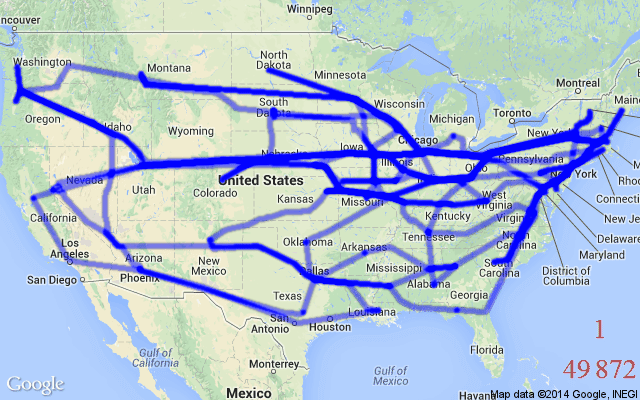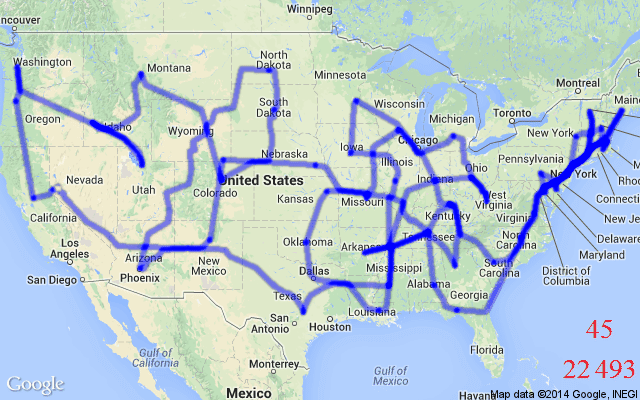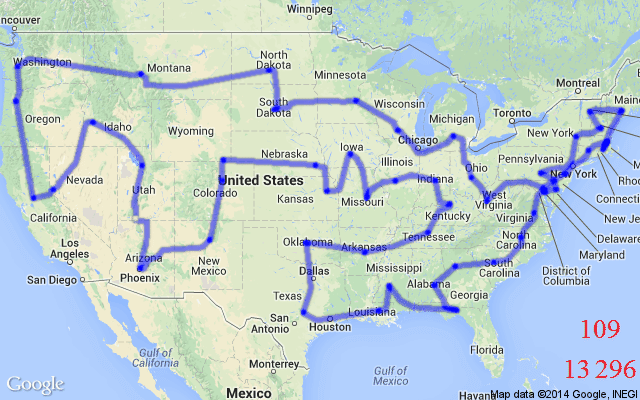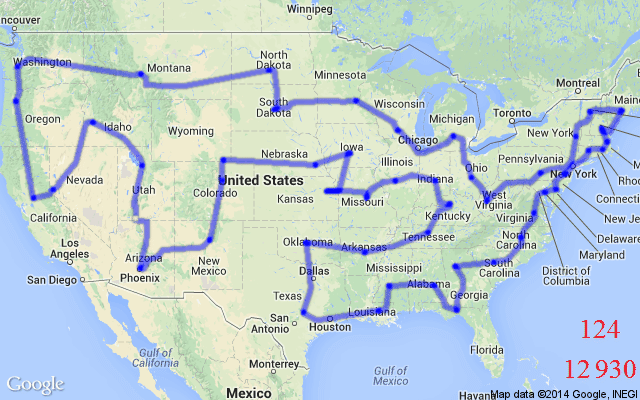
圖 1:TSP 提出以下問題:給定一個城市列表和每對城市之間的距離,銷售人員訪問每個城市并返回出發城市的最短路線是什么?(來源:MathGifs)
在現實世界和實際場景中,路由問題或車輛路由問題 (VRP) 可能會涉及超出普通的 TSP 的挑戰性約束。例如,帶有時間窗口的 TSP (TSPTW) 將「時間窗口」約束添加到 TSP 圖中的節點。這意味著某些節點只能在固定的時間間隔內訪問。另一種變體是,容量車輛路線問題 (CVRP) ,旨在為訪問一組客戶(即城市)的車隊(即多個銷售人員)找到最佳路線,每輛車都具有最大承載能力。
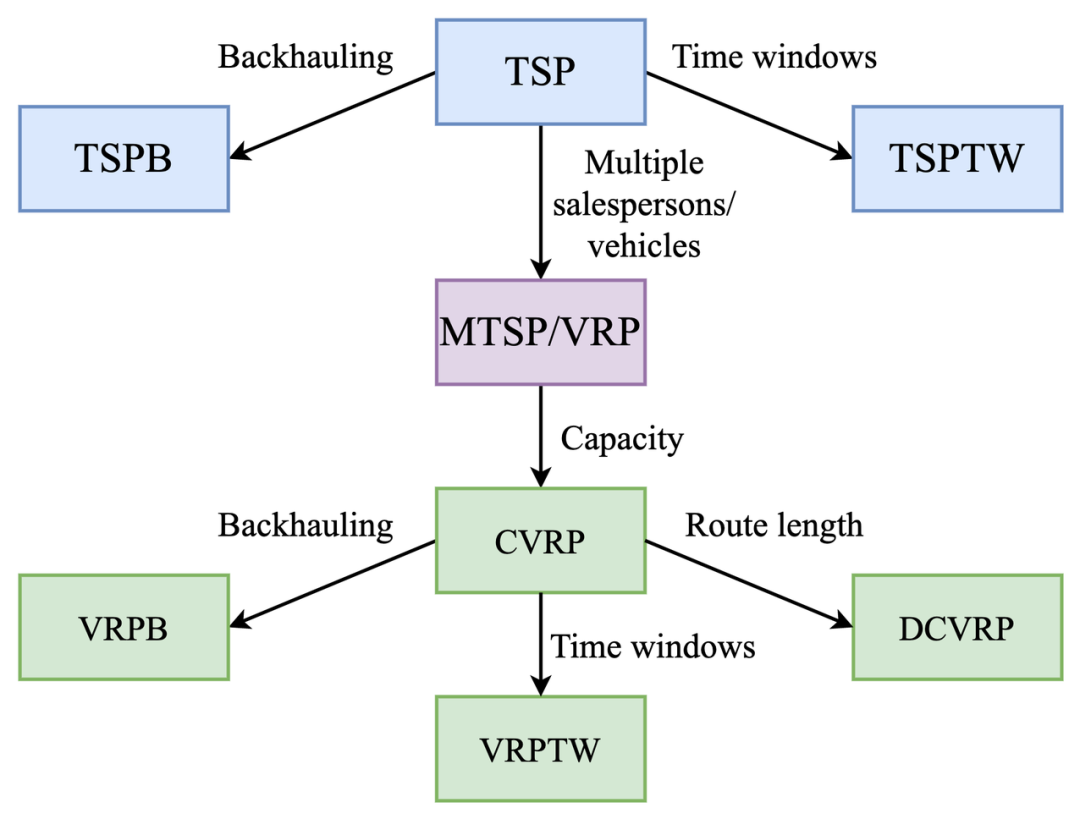
圖 2:TSP 和相關的車輛路徑問題類別。VRP 的約束的條件和 TSP 的不同,該圖呈現了相對充分研究的那些約束條件。在真實世界中可能存在具有更復雜和非標準約束的類 VRP 問題!(來源:改編自 Benslimane 和 Benadada,2014 年)
用深度學習解決路由問題
為路由問題開發可靠的算法和求解器需要大量的專家直覺和多年的反復試驗。例如,線性規劃、切割平面算法和分支定界問題中最先進的 TSP 求解器 Concorde 耗費了人們 50 多年的時間才得到;這是一段關于其歷史的鼓舞人心的視頻(https://www.youtube.com/watch?v=q8nQTNvCrjE)。Concorde 可以找到多達數萬個節點的最優解,但執行時間極長。正如讀者所想象的那樣,為復雜的 VRP 設計算法會更具挑戰性,也更耗時,尤其是在現實世界的限制條件下,例如混合容量或時間窗口問題。
于是,機器學習社區開始關注以下問題:
我們可以使用深度學習來讓解決 COP 所需的專家直覺流程自動化,甚至增強專家直覺嗎?有關更深入的動機,請參閱 Mila 的這項精妙調查:https://arxiv.org/abs/1811.06128
神經組合優化
如果把 COP 問題比作一根釘子,那么神經組合優化可以說是一種嘗試使用深度學習方法來解決問題的錘子。神經網絡經過訓練之后,可以直接從問題實例本身中學習來產生 COP 的近似解。這一系列研究始于 Google Brain 的開創性 Seq2seq 指針網絡和使用強化學習來實現神經組合優化的論文。如今,圖神經網絡通常是深度學習驅動的求解器的核心架構選擇,因為它們解決了這些問題相關的圖結構。
神經組合優化旨在通過以下方式改進傳統的 COP 求解器:
- 非手工的啟發式方法。神經網絡不需要應用專家手動設計啟發式和規則,而是通過模仿最佳求解器或通過強化學習來學習這些啟發式和規則(下一節中展示了一個示例)。
- GPU 快速推理。對于問題規模較大的情況,傳統求解器的執行時間通常很長,例如 Concorde 用了 7.5 個月的時間解決了擁有 109,399 個節點的最大 TSP。另一方面,一旦用來近似求解 COP 的神經網絡訓練完成,那么使用的時候就具有顯著有利的時間復雜度,并且可以通過 GPU 進行并行化。這使得它們非常適合解決實時決策問題,尤其是路由問題。
- 應對新穎且研究不足的 COP。神經組合優化可以顯著加快針對具有深奧約束的新問題或未研究問題的特定 COP 求解器的開發進度。此類問題經常出現在科學級的發現或計算機體系結構中,一個令人興奮的成功例子是谷歌的芯片設計系統,它將為下一代 TPU 提供動力。你沒看錯——下一個運行神經網絡的 TPU 芯片是由神經網絡設計的!
神經組合優化步驟
使用 TSP 作為典型示例,我們現在提出一個通用的神經組合優化步驟,可用于表征現代深度學習驅動的幾個路由問題的方法。
最先進的 TSP 方法將城市的原始坐標作為輸入,并利用 GNN 或 Transformer 結合經典圖搜索算法來建設性地構建近似解。其架構可以大致分為:(1)自回歸模型,以逐步的方式構建解集;(2) 非自回歸模型,一次性產生所有解。可以通過監督學習或通過強化學習最小化 TSP 遍歷的長度來訓練模型以模仿最佳求解器。 圖 3:神經組合優化步驟(來源:Joshi 等人,2021)。
圖 3:神經組合優化步驟(來源:Joshi 等人,2021)。
Joshi 等人在 2021 年提出的 5 階段步驟將突出的模型架構和學習范式整合到一個統一的框架中。這個步驟將使我們能夠剖析和分析深度學習在路由問題方面的最新發展,并為激勵未來的研究提供新的方向。
第一步通過圖定義問題
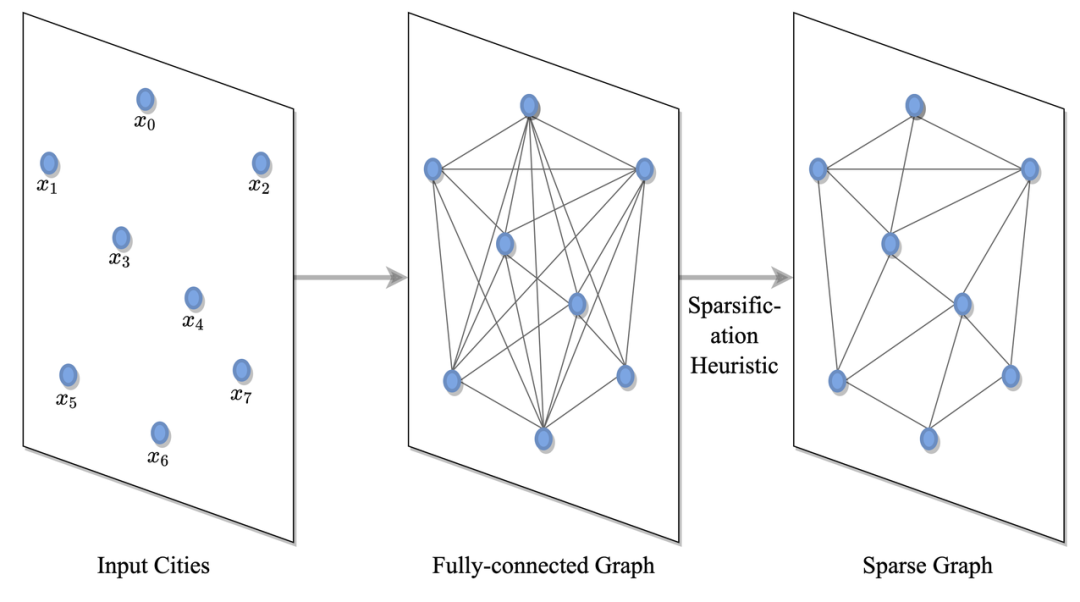 圖 4:問題定義:TSP 是通過城市 / 節點的全連接圖定義的,此圖可以進一步稀疏化。
圖 4:問題定義:TSP 是通過城市 / 節點的全連接圖定義的,此圖可以進一步稀疏化。
TSP 是通過一個全連接圖定義的,其中節點對應于城市,邊表示它們之間的道路。該圖可以通過啟發式算法(例如 k-nn 最近鄰算法)進行稀疏化。這使模型能夠擴展到所有節點的成對計算都難以處理的大型實例中 [Khalil 等人,2017 年],或者通過減少搜索空間來更快地學習 [Joshi 等人,2019 年]。
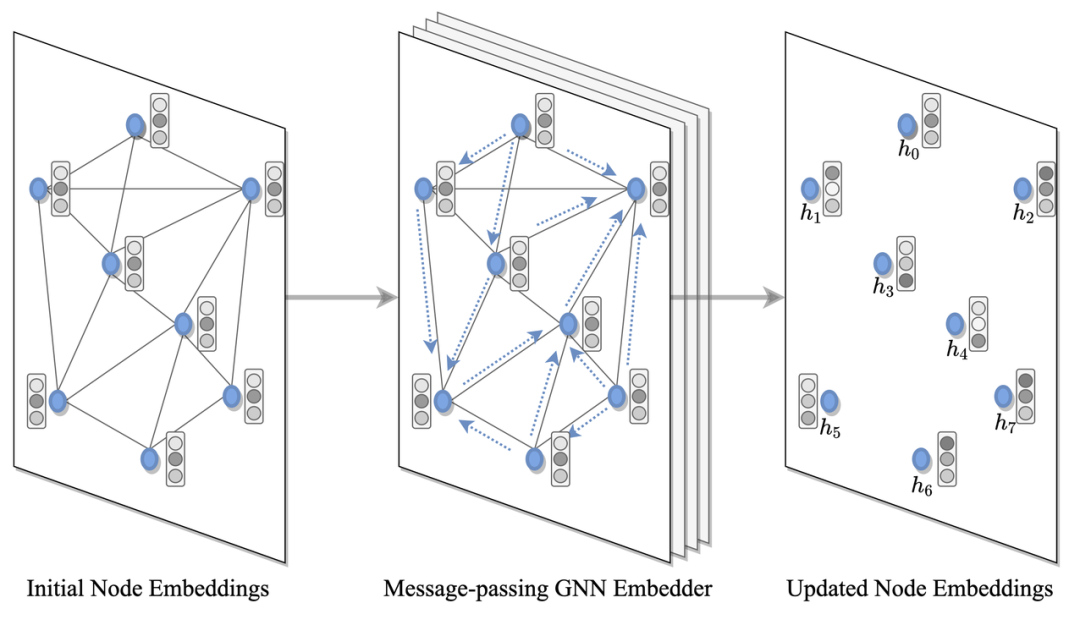
第二步:獲取圖節點和邊的隱空間嵌入
圖 5:圖嵌入:每個圖節點的嵌入是使用圖神經網絡編碼器獲得的,該編碼器通過遞歸聚合來自每個節點的鄰居的特征來構建局部結構特征。
GNN 或 Transformer 編碼器將 TSP 圖中的每個節點和邊,或者在兩者中選擇一個,作為輸入來計算隱空間表示或嵌入特征。在每一層當中,節點從其鄰居那里收集特征,再通過遞歸消息傳遞來表示局部圖結構。堆疊 L 層后,網絡就能從每個節點的 L 跳鄰域中構建節點的特征。
Transformers [Deudon et al., 2018, Kool et al., 2019] 和 Gated Graph ConvNets [Joshi et al., 2019] 等各向異性和基于注意力的 GNN 已成為編碼路由問題的默認選擇。鄰域聚合期間的注意力機制至關重要,因為它允許每個節點根據其對解決手頭任務的相對重要性來權衡其鄰居節點。
重要的是,Transformer 編碼器可以看作是全連接圖上的注意力 GNN,即圖注意力網絡 (GAT)。請參閱此博客文章以獲得直觀的解釋。
第三、四步:將嵌入轉換為離散解
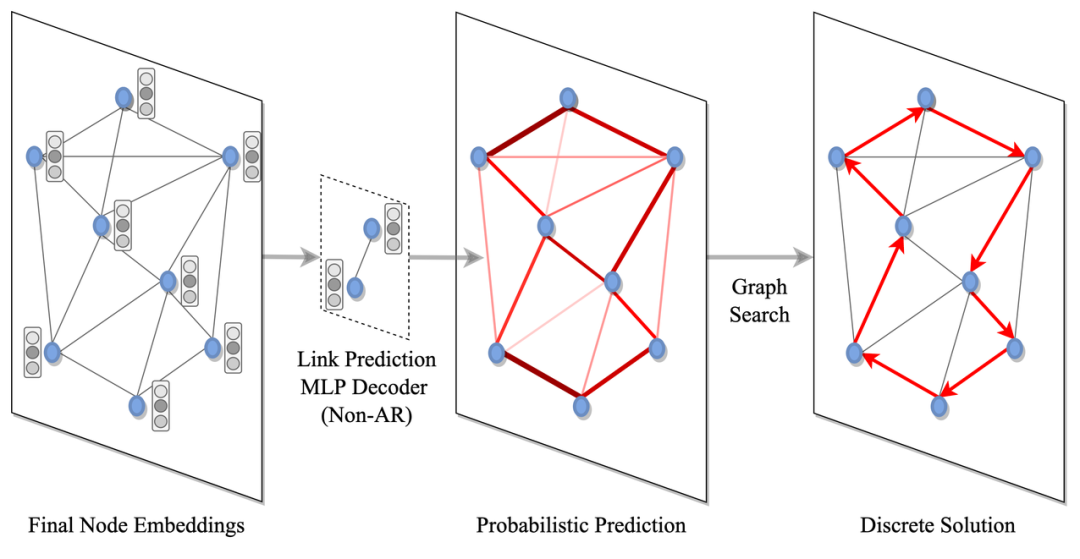
圖 5:解碼和搜索:為每個節點或每條邊分配屬于解集的概率(這里,MLP 對每條邊進行預測以獲得邊概率的「熱力圖」),然后轉換為離散決策中經典的圖搜索技術,例如貪心搜索或束搜索。
一旦圖的節點和邊被編碼為隱空間表示,我們必須將它們解碼為離散的 TSP 解決方法。具體來說,可以通過兩步過程完成:首先,將概率分配給每個節點或每條邊來將節點或邊添加到解集當中,無論是相互獨立地(即非自回歸解碼)或是通過圖遍歷有條件地(即自回歸解碼)。接下來,通過經典的圖搜索技術(例如由概率預測引導的貪心搜索或束搜索)將預測概率轉換為離散決策(稍后我們將在討論近期趨勢和未來方向時,討論更多關于圖搜索的內容)。
解碼器的選擇需要在數據效率和實現效率之間權衡:自回歸解碼器 [Kool et al., 2019] 將 TSP 轉換為 Seq2Seq 模型, 或基于一組無序城市節點的有序旅游路線的語言翻譯任務。他們通過每次選擇一個節點來明確地模擬路由問題的順序歸納偏差。另一方面,非自回歸解碼器 [Joshi et al., 2019] 將 TSP 視為生成邊緣概率熱力圖的任務。NAR 方法明顯更快,更適合實時推理,因為它是一次性而不是逐步地生成預測。然而,NAR 方法忽略了 TSP 的順序性,與 AR 解碼相比,訓練效率可能較低 [Joshi 等人,2021]。
第五步:模型訓練
最后,整個編碼器 - 解碼器模型以端到端的方式進行訓練,就像用于計算機視覺或自然語言處理的深度學習模型一樣。在最簡單的情況下,可以通過模仿最優求解器(即通過監督學習)來訓練模型以產生接近最優的解。對于 TSP,Concrode 求解器用于為數百萬個隨機實例生成最佳旅游路線的有標簽訓練數據集。帶有 AR 解碼器的模型通過強制教學(teacher-forcing )模式進行訓練,來輸出節點的最佳旅行序列 [Vinyals et al., 2015],而帶有 NAR 解碼器的模型經過訓練后,可以從未遍歷的邊集中識別出在旅行期間遍歷的邊 [Joshi et al., 2019]。
然而,為監督學習創建標記數據集是一個昂貴且耗時的過程。特別是對于大規模問題實例,最佳求解器在準確性上的保證可能不復存在,這會導致用于監督訓練的解決方案不精確。從實踐和理論的角度來看,這遠非是理想的方式 [Yehuda et al., 2020]。
對于未充分研究的問題來說,在缺乏標準解決方案的情況下,強化學習通常是一種優雅的替代方案。由于路由問題通常需要順序決策以最小化特定于問題的成本函數(例如 TSP 的旅行長度),它們可以優雅地投入 RL 框架中,該框架訓練智能體以最大化獎勵函數(損失函數的負值) . 帶有 AR 解碼器的模型可以通過標準策略梯度算法 [Kool et al., 2019] 或 Q 學習 [Khalil et al., 2017] 進行訓練。
各階段中的成果簡介
我們可以通過 5 階段步驟來描述 TSP 深度學習中的杰出成果。回想一下,步驟包括:(1)問題定義→(2)圖嵌入→(3)解碼→(4)解搜索→(5)策略學習。下表從 Oriol Vinyals 及其合作者發表的指針網絡論文開始介紹,紅色突出表示該論文具有主要創新和貢獻。
未來工作的最新進展和途徑
有了統一的 5 階段步驟,我們接下來重點介紹深度學習路由問題的一些最新進展和趨勢。同時還將提供一些未來的研究方向,重點探討如何提高對大規模和真實世界實例的泛化能力。
利用等方差和對稱性
作為最有影響力的早期作品之一,自回歸注意力模型 [Kool et al., 2019] 將 TSP 視為可以用 Seq2Seq 解決的語言翻譯問題,并將 TSP 旅行順序構建為城市排列。該公式的一個直接缺點是它沒有考慮路由問題的潛在對稱性。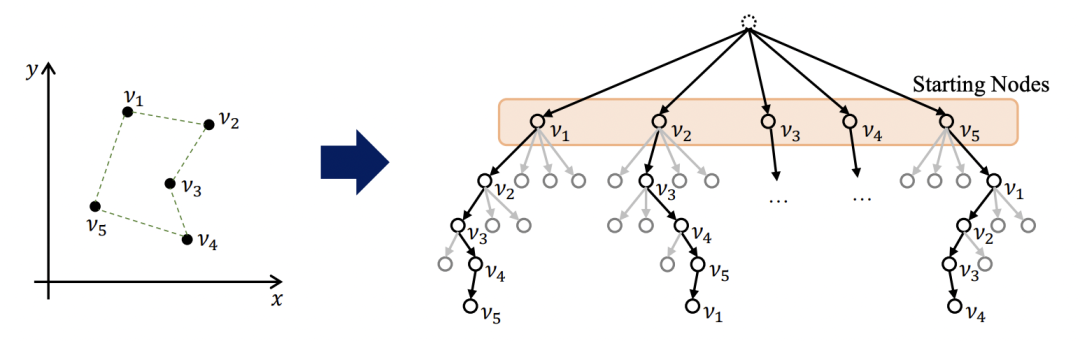 圖 6:一般來說,TSP 有一個唯一的最優解 (L)。然而,在自回歸公式下,當解表示為節點序列時,存在多個最優排列 (R)。(來源:Kwon 等人,2020)
圖 6:一般來說,TSP 有一個唯一的最優解 (L)。然而,在自回歸公式下,當解表示為節點序列時,存在多個最優排列 (R)。(來源:Kwon 等人,2020)
POMO: Policy Optimization with Multiple Optima [Kwon et al., 2020] 建議在建設性自回歸公式中利用起始城市的不變性。他們訓練了與之前相同的注意力模型,但不同之處在于他們使用了一種新的強化學習算法(上述步驟中的第 5 步),該算法利用了多個最優旅行排列。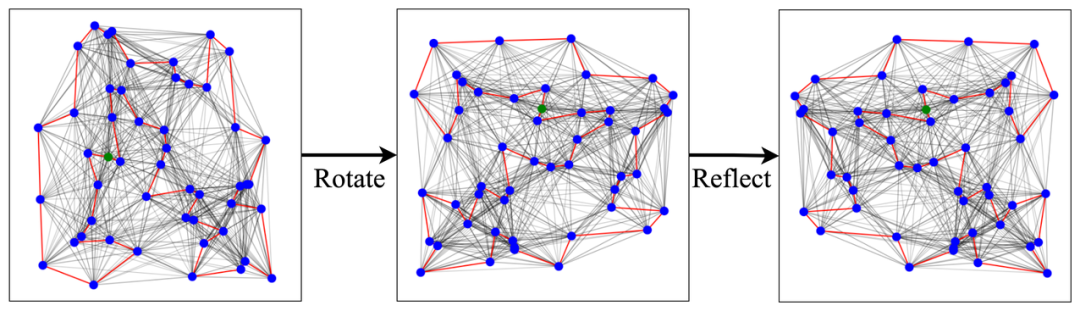 圖 7:在旋轉、反射和轉換后,城市坐標的歐幾里得對稱群的 TSP 解保持不變。將這些對稱性納入模型可能是解決大規模 TSP 的原則性方法。
圖 7:在旋轉、反射和轉換后,城市坐標的歐幾里得對稱群的 TSP 解保持不變。將這些對稱性納入模型可能是解決大規模 TSP 的原則性方法。
同樣地,Ouyang 等人在 2021 年對注意力模型進行了升級,考慮了輸入城市坐標的旋轉、反射和平移(即歐幾里得對稱群)的不變性。他們提出了一種自回歸方法,通過同時在問題定義階段(步驟 1)執行數據增強并在圖形編碼(步驟 2)期間使用相對坐標來確保不變性。他們在 TSPLib 數據集上進行的從隨機實例到現實世界的零樣本泛化實驗顯示他們的模型具有很好的效果。
未來的工作可能會在架構設計上遵循幾何深度學習 (GDL) 藍圖。GDL 告訴我們要明確考慮數據或問題的對稱性和歸納偏差,并將其結合起來。由于路由問題需要被嵌入在歐幾里得坐標中,以及路由是循環的,因此將這些約束直接納入模型架構或學習范式可能是一種原則性方法,可以提高對比訓練期間更大的大規模實例的泛化能力。
改進后的圖搜索算法
另一個有影響力的研究方向是一次性非自回歸圖卷積網絡方法 [Joshi et al., 2019]。最近的幾篇論文提出保留相同的門控 GCN 編碼器(步驟 2),同時用更強大和靈活的圖搜索算法替換束搜索組件(步驟 4),例如動態規劃 [Kool et al., 2021] 或蒙特卡洛樹搜索 (MCTS) [Fu et al., 2020]。 圖 8:門控 GCN 編碼器 [Joshi 等人,2019 年] 可用于為 TSP、CVRP 和 TSPTW 生成邊預測「熱力圖」(透明紅色)。這些可以由 DP 或 MCTS 進一步處理以輸出路由(純色)。GCN 從本質上減少了復雜搜索算法的解搜索空間,復雜搜索算法在搜索所有可能的路線時可能難以處理。(資料來源:Kool 等人,2021 年)
圖 8:門控 GCN 編碼器 [Joshi 等人,2019 年] 可用于為 TSP、CVRP 和 TSPTW 生成邊預測「熱力圖」(透明紅色)。這些可以由 DP 或 MCTS 進一步處理以輸出路由(純色)。GCN 從本質上減少了復雜搜索算法的解搜索空間,復雜搜索算法在搜索所有可能的路線時可能難以處理。(資料來源:Kool 等人,2021 年)
Fu 等人提出的 GCN + MCTS 框架有一種非常有趣的方法,該方法可以在很小的 TSP 問題上有效地訓練模型,并以零樣本的方式(類似 Joshi 等人最初探究的 GCN + 束搜索方式)成功地將學習的策略轉移到更大的圖上。他們通過更新問題定義(步驟 1)來確保 GCN 編碼器的預測結果可以在 TSP 從小到大變化時仍然具有泛化能力:規模較大的問題實例被表示為許多較小的子圖,這些子圖的大小與 GCN 的訓練圖相同,然后在執行 MCTS 之前合并 GCN 的邊預測結果。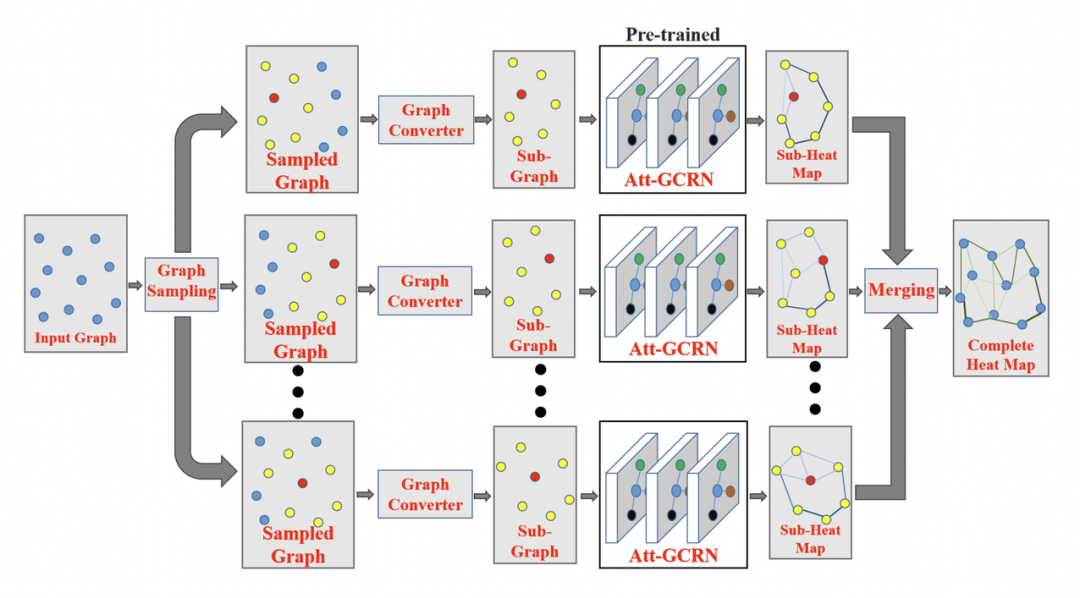 圖 9:GCN + MCTS 框架 [Fu et al., 2020] 將大型 TSP 問題表示為一組與用于訓練的 GCN 的圖大小相同的規模較小的子圖。將 GCN 預測得到的子圖的邊熱力圖合并在一起,可以獲得原圖的熱圖。這種分而治之的方法確保了 GCN 的嵌入和預測能夠很好地從較小的實例推廣到較大的實例。(來源:Fu et al., 2020)
圖 9:GCN + MCTS 框架 [Fu et al., 2020] 將大型 TSP 問題表示為一組與用于訓練的 GCN 的圖大小相同的規模較小的子圖。將 GCN 預測得到的子圖的邊熱力圖合并在一起,可以獲得原圖的熱圖。這種分而治之的方法確保了 GCN 的嵌入和預測能夠很好地從較小的實例推廣到較大的實例。(來源:Fu et al., 2020)
這種分而治之的策略最初由 Nowak 等人在 2018 年提出,以確保 GNN 的嵌入和預測能夠很好地泛化從較小到較大的 TSP 實例(最多 10,000 個節點)。將 GNN、分而治之和搜索策略融合在一起,來處理多達 3000 個節點的大規模 CVRP 問題同樣充滿無限可能。[Li et al., 2021]。
總體而言,這一系列的工作表明,模型的神經元和符號 / 搜索組件的設計之間的更強耦合對于分布外泛化至關重要 [Lamb 等人,2020]。然而,同樣值得注意的是,在 GPU 上實現圖搜索的設計高度定制化和并行化,可能對每個新問題都是一種挑戰。
學習改進次優解
最近,從 Chen 等人在 2019 的工作和 Wu 等人在 2021 年的工作開始,許多論文探索了建設性的 AR 和 NAR 解的替代方案,包括迭代改進(次優)解學習或局部搜索學習。其他著名論文包括 Cappart et al., 2021, da Costa et al., 2020, Ma et al., 2021, Xin et al., 2021 和 Hudson et al., 2021.。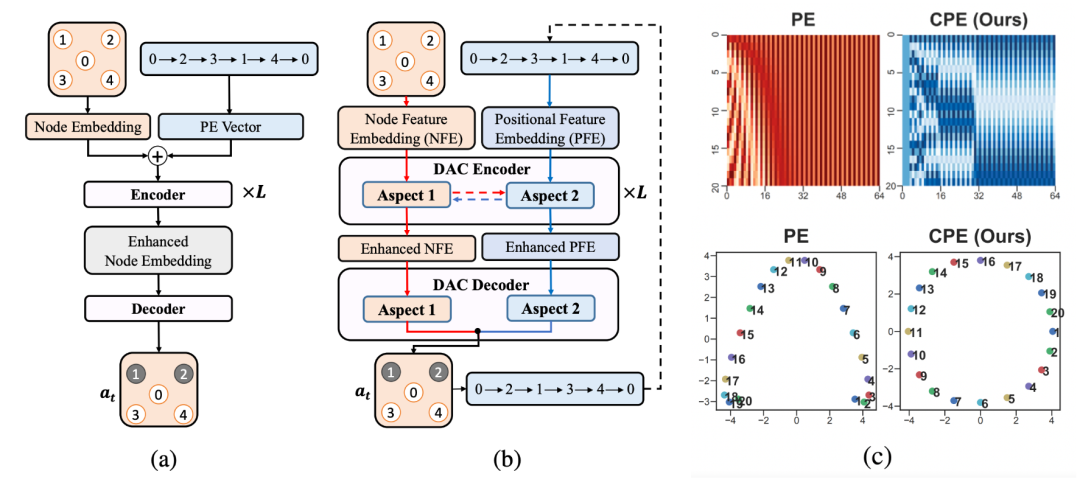 圖 10:通過在局部搜索算法中的指導決策來學習改進次優 TSP 解的架構。(a) 原始的 Transformer 編碼器 - 解碼器架構 [Wu et al., 2021],該方法使用正弦位置編碼來表示當前的次優旅行排列;(b) Ma et al., 2021 通過在對稱性問題上做了進一步的升級:具有可學習的位置編碼的雙端 Transformer 編碼器 - 解碼器,能夠捕捉 TSP 旅行的循環性質;(c) 正弦曲線與周期性位置編碼的可視化。
圖 10:通過在局部搜索算法中的指導決策來學習改進次優 TSP 解的架構。(a) 原始的 Transformer 編碼器 - 解碼器架構 [Wu et al., 2021],該方法使用正弦位置編碼來表示當前的次優旅行排列;(b) Ma et al., 2021 通過在對稱性問題上做了進一步的升級:具有可學習的位置編碼的雙端 Transformer 編碼器 - 解碼器,能夠捕捉 TSP 旅行的循環性質;(c) 正弦曲線與周期性位置編碼的可視化。
在所有這些工作中,由于深度學習用于指導經典局部搜索算法中的決策(這些算法被設計為無論問題規模如何都能工作),因此與建設性方法相比,這種方法隱含地導致對更大問題實例的更好的零樣本泛化。實際來說,這是一個非常理想的屬性,因為在非常大或真實世界的 TSP 實例上進行訓練可能很棘手。
值得注意的是,NeuroLKH [Xin et al., 2021] 使用通過 GNN 生成的邊概率熱力圖來改進經典的 Lin-Kernighan-Helsgaun 算法,并展示了對具有 5000 個節點的 TSP 以及跨對 TSPLib 數據集中,實例的強大零樣本泛化能力。
這項工成果的限制之一是需要事先手工設計的局部搜索算法,對于新的或未充分研究的問題可能是會缺少的。另一方面,通過在解碼和搜索過程中實施約束,建設性的方法可以說更容易適應新問題。
促進泛化的學習范式
未來的工作可以著眼于新的學習范式(步驟 5),這些范式明確關注監督和強化學習之外的泛化,例如 Hottung et al., 2020 探索了自動編碼器目標,以學習路由問題解的連續空間,而 Geisler et al., 2021 訓練神經求解器,使其對對抗性擾動具有魯棒性。
目前,大多數論文都建議在非常小的隨機 TSP 上有效地訓練模型,然后以零樣本的方式將學習到的策略轉移到更大的圖和真實世界的實例中。合乎邏輯的下一步是在少數特定問題實例上微調模型。Hottung et al., 2021 在 2021 年邁出了第一步,建議通過主動搜索為每個特定問題實例微調模型參數的子集。在未來的工作中,將微調作為元學習問題進行探索可能會很有趣,元學習問題的目標是訓練模型參數,用于快速適應新的數據分布和問題。
另一個有趣的可以探索的方向是通過對流行的路由問題(如 TSP 和 CVPR)進行多任務預訓練,然后針對特定問題的微調來解決具有挑戰性約束的未充分研究的路由問題。與自然語言處理中作為預訓練目標的語言建模類似,路由預訓練的目標是學習通常來說會有用的潛在表示,這些表示可以很好地轉移到新的路由問題上。
改進后的評估協議
除了算法創新之外,社區一再呼吁推出更現實的評估協議,這可以推動現實世界路由問題的進步和工業界的落實 [Francois et al., 2019, Yehuda et al., 2020]。最近, Accorsi et al., 2021 為實驗設計和與經典運籌學 (OR) 技術的比較提供了一套權威指南。他們希望對標準化基準進行公平和嚴格的比較將成為將深度學習技術集成到工業路由求解器中的第一步。
總的來說,令人鼓舞的是,近期的論文不僅顯示了對微小的隨機 TSP 實例的輕微性能提升,而且還采用了 TSPLib 和 CVPRLib 等真實世界的基準測試數據集。此類路由問題集合包含來自全球城市和道路網絡的圖表及其精確解決方案,并已成為 OR 社區中新求解器的標準測試平臺。
同時,我們必須在其他論文都在使用的前 n 個 TSPLib 或 CVPRLib 實例上不「過擬合」。因此,更好的合成數據集與公平的基準測試進展密切相關,例如 Queiroga et al., 2021 (https://openreview.net/forum?id=yHiMXKN6nTl) 最近提出了一個新的合成 了 10,000 個 CVPR 測試實例的庫。
?
圖 11:關注 ML4CO 等社區競賽能有效地跟蹤研究進展。(來源:ML4CO 網站)。對新構造的現實世界數據集進行定期競賽,例如 NeurIPS 2021 的 ML4CO 競賽和 IJCAI 2021 的 AI4TSP,也是跟蹤深度學習和路由問題交叉點進展的一個有效手段。
我們強烈呼吁能夠在 YouTube 上獲取來自 ML4CO、NeurIPS 2021 的有價值的小組討論和演講。
總結
這篇博文介紹了一系列神經組合優化步驟,這些步驟將最近關于深度學習的論文統一到一個單一的框架中。然后,通過此框架的視角,我們分析和剖析最近的研究進展,并預測未來研究的方向。
最后一點想說的是,神經組合優化的更深刻的研究動機可能并不是為了在經過充分研究的路由問題上勝過經典方法。神經網絡可以用作解決以前未遇到的 NP 難問題的通用工具,尤其是那些對于設計啟發式算法而言并非微不足道的問題。我們贊嘆神經組合優化最近在設計計算機芯片、優化通信網絡和基因組重建方面的應用,并期待未來有更多有價值的應用!