打破「反向傳播」壟斷,「正向自動微分」也能計算梯度,且訓練時間減少一半
本文轉自雷鋒網,如需轉載請至雷鋒網官網申請授權。
反向傳播和基于梯度的優化是近年來機器學習(ML)取得重大突破的核心技術。
人們普遍認為,機器學習之所以能夠快速發展,是因為研究者們使用了第三方框架(如PyTorch、TensorFlow)來解析ML代碼。這些框架不僅具有自動微分(AD)功能,還為本地代碼提供了基礎的計算功能。而ML所依賴的這些軟件框架都是圍繞 AD 的反向模式所構建的。這主要是因為在ML中,當輸入的梯度為海量時,可以通過反向模式的單次評估進行精確有效的評估。
自動微分算法分為正向模式和反向模式。但正向模式的特點是只需要對一個函數進行一次正向評估(即沒有用到任何反向傳播),計算成本明顯降低。為此,來自劍橋與微軟等機構的研究者們探索這種模式,展示了僅使用正向自動微分也能在一系列機器學習框架上實現穩定的梯度下降。

論文地址:https://arxiv.org/pdf/2202.08587v1.pdf他們認為,正向梯度有利于改變經典機器學習訓練管道的計算復雜性,減少訓練的時間和精力成本,影響機器學習的硬件設計,甚至對大腦中反向傳播的生物學合理性產生影響。
1 自動微分的兩種模式
首先,我們來簡要回顧一下自動微分的兩種基本模式。
正向模式
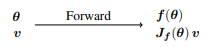
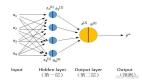
給定一個函數 f: θ∈R n,v∈R n,正向模式的AD會計算 f(θ) 和雅可比向量乘積Jf (θ) v,其中Jf (θ) ∈R m×n是f在θ處評估的所有偏導數的雅可比矩陣,v是擾動向量。對于 f : R n → R 的情況,在雅可比向量乘積對應的方向導數用 ?f(θ)- v表示,即在θ處的梯度?f對方向向量v的映射,代表沿著該方向的變化率。值得注意的是,正向模式在一次正向運行中同時評估了函數 f 及其雅可比向量乘積 Jf v。此外,獲得 Jf v 不需要計算雅可比向量Jf,這一特點被稱為無矩陣計算。
反向模式
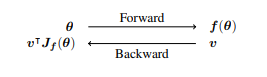
給定一個函數 f : R n → R m,數值 θ∈R n,v∈R m,AD反向模式會計算f(θ)和雅可比向量乘積v |Jf (θ),其中Jf∈R m×n是f在θ處求值的所有偏導數的雅可比矩陣,v∈R m是一個鄰接的矢量。對于f : R n → R和v = 1的情況,反向模式計算梯度,即f對所有n個輸入的偏導數?f(θ)=h ?f ?θ1,. . . , ?f ?θn i| 。請注意,v |Jf 是在一次前向-后向評估中進行計算的,而不需要計算雅可比Jf 。
運行時間成本
兩種AD模式的運行時間以運行正在微分的函數 f 所需時間的恒定倍數為界。反向模式的成本比正向模式高,因為它涉及到數據流的反轉,而且需要保留正向過程中所有操作結果的記錄,因為在接下來的反向過程中需要這些記錄來評估導數。內存和計算成本特征最終取決于AD系統實現的功能,如利用稀疏性。成本可以通過假設基本操作的計算復雜性來分析,如存儲、加法、乘法和非線性操作。將評估原始函數 f 所需的時間表示設為 runtime(f),我們可以將正向和反向模式所需的時間分別表示為 Rf×runtime(f) 和 Rb×runtime(f)。在實踐中,Rf 通常在1到3之間,Rb通常在5到10之間,不過這些結果都與程序高度相關。
2 方法
正向梯度
定義1
給定一個函數 f : R n → R,他們將「正向梯度」 g : R n → R n 定義為:
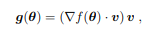
其中,θ∈R n 是評估梯度的關鍵點,v∈R n 是一個擾動向量,被視為一個多元隨機變量v~p(v),這樣 v 的標量分量 vi 是獨立的,對所有 i 都有零均值和單位方差,?f(θ)-v∈R 是 f 在在 v 方向上 θ 點的方向導數。
簡要地談一下這個定義的由來。
如前所述,正向模式直接給我們提供了方向導數?f(θ) - v = P i ?f ?θi vi,無需計算?f。將 f 正向評估 n 次,方向向量取為標準基(獨熱碼)向量ei∈R n,i=1 ... n,其中ei表示在第i個坐標上為1、其他地方為0的向量,這時,只用正向模式就可以計算?f。
這樣就可以分別評估f對每個輸入?f ?θi的敏感性,把所有結果合并后就可以得到梯度?f。為了獲得比反向傳播更優的運行時間優勢,我們需要在每個優化迭代中運行一次正向模式。在一次正向運行中,我們可以將方向v理解為敏感度加權和中的權重向量,即P i ?f ?θi vi,盡管這沒辦法區分每個θi在最終總數中的貢獻。因此,我們使用權重向量v將總體敏感度歸因于每個單獨的參數θi,與每個參數θi的權重vi成正比(例如,權重小的參數在總敏感度中的貢獻小,權重大的參數貢獻大)。
總之,每次評估正向梯度時,我們只需做以下工作:
- 對一個隨機擾動向量v~p(v)進行采樣,其大小與f的第一個參數相同。
- 通過AD正向模式運行f函數,在一次正向運行中同時評估f(θ)和?f(θ)-v,在此過程中無需計算?f。得到的方向導數(?f(θ)-v)是一個標量,并且由AD精確計算(不是近似值)。
- 將標量方向導數?f(θ)-v與矢量v相乘,得到g(θ),即正向梯度。
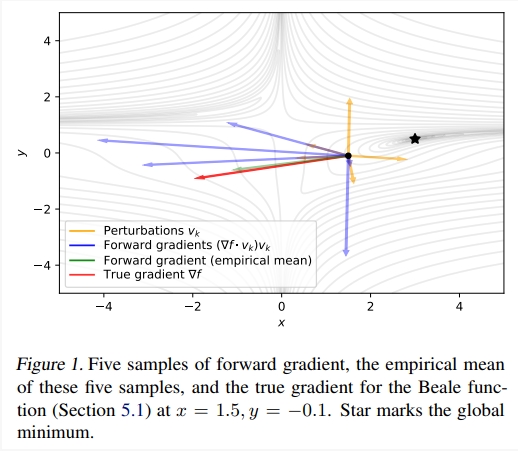
圖 1 顯示了 Beale函數的幾個正向梯度的評估結果。我們可以看到擾動vk(橙色)如何在k∈[1,5]的情況下轉化為正向梯度(?f-vk)vk(藍色),在受到指向限制時偶爾也會指向正確的梯度(紅色)。綠色箭頭表示通過平均正向梯度來評估蒙特卡洛梯度,即1 K PK k=1(?f - vk)vk≈E[(?f - v)v]。
正向梯度下降
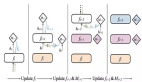
他們構建了一個正向梯度下降(FGD)算法,用正向梯度g代替標準梯度下降中的梯度?f(算法1)。
在實踐中,他們使用小型隨機版本,其中 ft 在每次迭代中都會發生變化,因為它會被訓練中使用的每一小批數據影響。研究者注意到,算法 1 中的方向導數dt可以為正負數。如果為負數,正向梯度gt的方向會發生逆轉,指向預料中的真實梯度。圖1顯示的兩個vk樣本,證明了這種行為。
在本文中,他們將范圍限制在FGD上,單純研究了這一基礎算法,并將其與標準反向傳播進行比較,不考慮動量或自適應學習率等其他各種干擾因素。筆者認為,正向梯度算法是可以應用到其他基于梯度算法的優化算法系列中的。

3 實驗
研究者在PyTorch中執行正向AD來進行實驗。他們發現,正向梯度與反向傳播這兩種方法在內存上沒有實際差異(每個實驗的差異都小于0.1%)。
邏輯回歸
圖 3 給出了多叉邏輯回歸在MNIST數字分類上的幾次運行結果。我們觀察到,相比基本運行時間,正向梯度和反向傳播的運行時間成本分別為 Rf=2.435 和 Rb=4.389,這與人們對典型AD系統的預期相符。
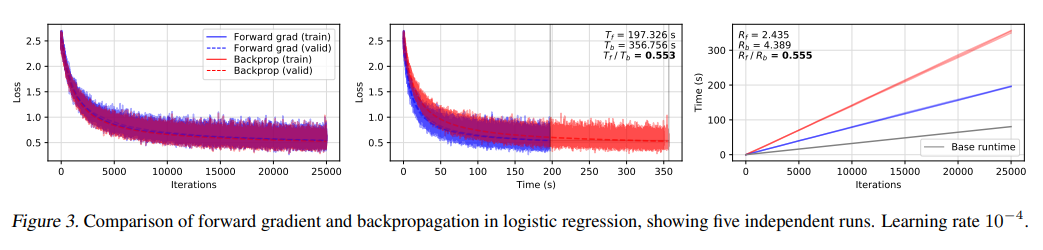
Rf/Rb=0.555和Tf/Tb=0.553的比率表明,在運行時間和損失性能方面,正向梯度大約比反向傳播快兩倍。
在簡單的模型中,這些比率是一致的,因為這兩種技術在空間行為的迭代損失上幾乎相同,這意味著運行時收益幾乎直接反映在每個時間空間的損失上。
多層神經網絡
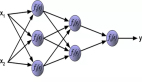
圖4顯示了用多層神經網絡在不同學習率下進行MNIST分類的兩個實驗。他們使用了三個架構大小分別為1024、1024、10的全連接層。在這個模型架構中,他們觀察到正向梯度和反向傳播相對于基礎運行時間的運行成本為Rf=2.468和Rb=4.165,相對測量 Rf/Rb 平均為0.592,與邏輯回歸的情況大致相同。
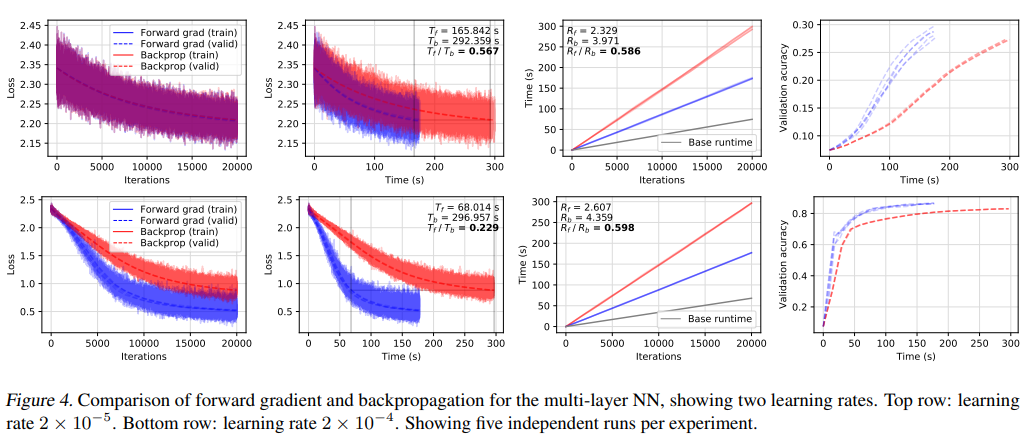
有趣的是,在第二個實驗中(學習率為2×10-4),我們可以看到正向梯度在每個迭代損失圖中都實現了快速的下降。作者認為,這種行為是由于常規SGD(反向傳播)和正向SGD算法的隨機性不同所導致的,因此他們推測:正向梯度引入的干擾可能有利于探索損失平面。
我們可以從時間曲線圖看到,正向模式減少了運行時間。我們看到,損失性能指標Tf/Tb值為0.211,這表明在驗證實驗損失的過程中,正向梯度的速度是反向傳播的四倍以上。
卷積神經網絡
圖 5 展示了一個卷積神經網絡對同一MNIST分類任務的正向梯度和反向傳播的比較。在這個架構中,他們觀察到,相對于基本運行時間,正向AD的性能最好,其中正向模式的Rf=1.434,代表了在基本運行時間之上的開銷只有 43%。Rb=2.211 的反向傳播非常接近反向 AD 系統中所期待的理想情況。Rf/Rb=0.649 代表了正向AD運行時間相對于反向傳播的一個顯著優勢。在損失空間,他們得到一個比率 Tf /Tb=0.514,這表明在驗證損失的實驗中,正向梯度的速度比反向傳播的速度要快兩倍。
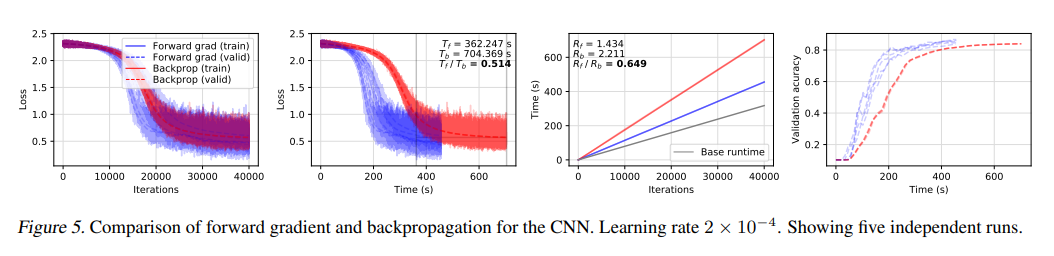
可擴展性
前面的幾個結果表明:
- 不用反向傳播也可以在一個典型的ML訓練管道中進行訓練,并且以一種競爭計算的方式來實現;
- 在相同參數(學習率和學習率衰減)的情況下,正向AD比反向傳播所消耗的時間要少很多。
相對于基礎運行時的成本,我們看到,對于大部分實驗,反向傳播在Rb∈[4,5]內,正向梯度在Rf∈[3,4]內。我們還觀察到,正向梯度算法在整個范圍內對運行都是有利的。Rf/Rb比率在10層以內保持在0.6以下,在100層時略高于0.8。重要的是,這兩種方法在內存消耗上幾乎沒有差別。
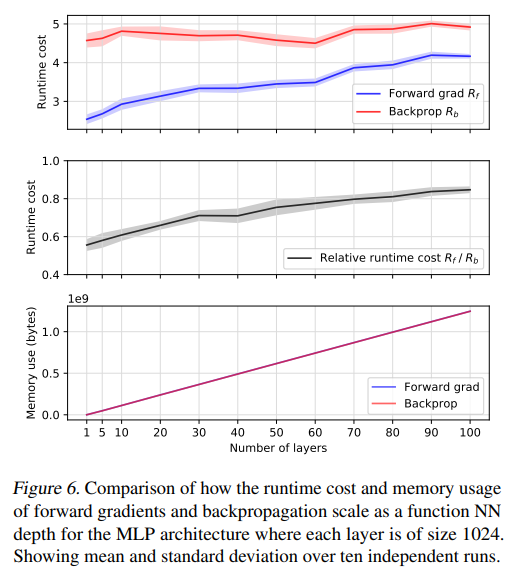
4 結論
總的來說,這篇工作的幾點貢獻主要如下:
- 他們將「正向梯度」(forward gradient)定義為:一個無偏差的、基于正向自動微分且毫不涉及到反向傳播的梯度估算器。
- 他們在PyTorch中從零開始,實現了正向模式的自動微分系統,且完全不依賴PyTorch中已有的反向傳播。
- 他們把正向梯度模式應用在各類隨機梯度下降(SGD)優化中,最后的結果充分證明了:一個典型的現代機器學習訓練管道可以只使用自動微分正向傳播來構建。
- 他們比較了正向梯度和反向傳播的運行時間和損失消耗等等,證明了在一些情況下,正向梯度算法的速度比反向傳播快兩倍。