[[443068]]

使用最小花費爬樓梯

力扣題目鏈接：https://leetcode-cn.com/problems/min-cost-climbing-stairs

數組的每個下標作為一個階梯，第 i 個階梯對應著一個非負數的體力花費值 cost[i](下標從 0 開始)。

每當你爬上一個階梯你都要花費對應的體力值，一旦支付了相應的體力值，你就可以選擇向上爬一個階梯或者爬兩個階梯。

請你找出達到樓層頂部的最低花費。在開始時，你可以選擇從下標為 0 或 1 的元素作為初始階梯。

示例 1：

• 輸入：cost = [10, 15, 20]
• 輸出：15
• 解釋：最低花費是從 cost[1] 開始，然后走兩步即可到階梯頂，一共花費 15 。

示例 2：

• 輸入：cost = [1, 100, 1, 1, 1, 100, 1, 1, 100, 1]
• 輸出：6
• 解釋：最低花費方式是從 cost[0] 開始，逐個經過那些 1 ，跳過 cost[3] ，一共花費 6 。

提示：

• cost 的長度范圍是 [2, 1000]。
• cost[i] 將會是一個整型數據，范圍為 [0, 999] 。

思路

這道題目可以說是昨天動態規劃：爬樓梯的花費版本。

注意題目描述：每當你爬上一個階梯你都要花費對應的體力值，一旦支付了相應的體力值，你就可以選擇向上爬一個階梯或者爬兩個階梯

所以示例1中只花費一個15 就可以到階梯頂，最后一步可以理解為 不用花費。

讀完題大家應該知道指定需要動態規劃的，貪心是不可能了。

確定dp數組以及下標的含義

使用動態規劃，就要有一個數組來記錄狀態，本題只需要一個一維數組dp[i]就可以了。

dp[i]的定義：到達第i個臺階所花費的最少體力為dp[i]。(注意這里認為是第一步一定是要花費)

對于dp數組的定義，大家一定要清晰!

確定遞推公式

可以有兩個途徑得到dp[i]，一個是dp[i-1] 一個是dp[i-2]。

那么究竟是選dp[i-1]還是dp[i-2]呢?

一定是選最小的，所以dp[i] = min(dp[i - 1], dp[i - 2]) + cost[i];

注意這里為什么是加cost[i]，而不是cost[i-1],cost[i-2]之類的，因為題目中說了：每當你爬上一個階梯你都要花費對應的體力值

dp數組如何初始化

根據dp數組的定義，dp數組初始化其實是比較難的，因為不可能初始化為第i臺階所花費的最少體力。

那么看一下遞歸公式，dp[i]由dp[i-1]，dp[i-2]推出，既然初始化所有的dp[i]是不可能的，那么只初始化dp[0]和dp[1]就夠了，其他的最終都是dp[0]dp[1]推出。

所以初始化代碼為：

vector<int> dp(cost.size()); 
dp[0] = cost[0]; 
dp[1] = cost[1]; 

確定遍歷順序

最后一步，遞歸公式有了，初始化有了，如何遍歷呢?

本題的遍歷順序其實比較簡單，簡單到很多同學都忽略了思考這一步直接就把代碼寫出來了。

因為是模擬臺階，而且dp[i]又dp[i-1]dp[i-2]推出，所以是從前到后遍歷cost數組就可以了。

但是稍稍有點難度的動態規劃，其遍歷順序并不容易確定下來。

例如：01背包，都知道兩個for循環，一個for遍歷物品嵌套一個for遍歷背包容量，那么為什么不是一個for遍歷背包容量嵌套一個for遍歷物品呢?以及在使用一維dp數組的時候遍歷背包容量為什么要倒敘呢?

這些都是遍歷順序息息相關。當然背包問題后續「代碼隨想錄」都會重點講解的!

舉例推導dp數組

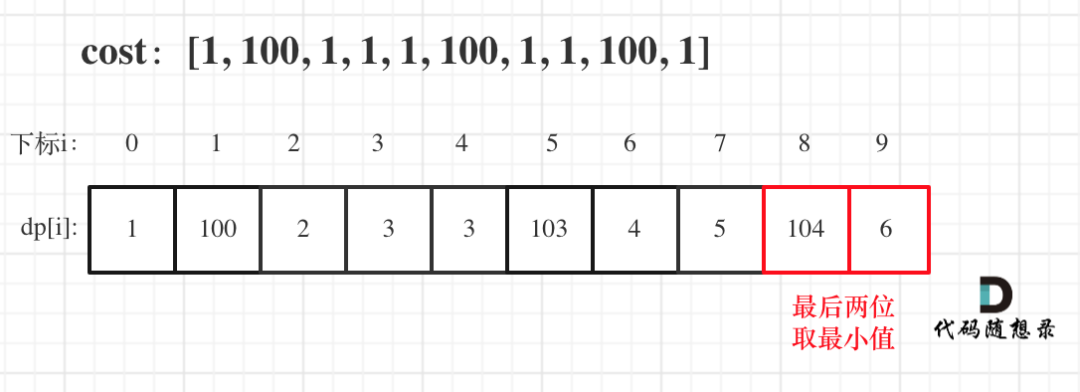
拿示例2：cost = [1, 100, 1, 1, 1, 100, 1, 1, 100, 1] ，來模擬一下dp數組的狀態變化，如下：

使用最小花費爬樓梯

如果大家代碼寫出來有問題，就把dp數組打印出來，看看和如上推導的是不是一樣的。

以上分析完畢，整體C++代碼如下：

// 版本一 
class Solution { 
public: 
    int minCostClimbingStairs(vector<int>& cost) { 
        vector<int> dp(cost.size()); 
        dp[0] = cost[0]; 
        dp[1] = cost[1]; 
        for (int i = 2; i < cost.size(); i++) { 
            dp[i] = min(dp[i - 1], dp[i - 2]) + cost[i]; 
        } 
        // 注意最后一步可以理解為不用花費，所以取倒數第一步，第二步的最少值 
        return min(dp[cost.size() - 1], dp[cost.size() - 2]); 
    } 
}; 

• 時間復雜度：
• 空間復雜度：

還可以優化空間復雜度，因為dp[i]就是由前兩位推出來的，那么也不用dp數組了，C++代碼如下：

// 版本二 
class Solution { 
public: 
    int minCostClimbingStairs(vector<int>& cost) { 
        int dp0 = cost[0]; 
        int dp1 = cost[1]; 
        for (int i = 2; i < cost.size(); i++) { 
            int dpi = min(dp0, dp1) + cost[i]; 
            dp0 = dp1; // 記錄一下前兩位 
            dp1 = dpi; 
        } 
        return min(dp0, dp1); 
    } 
}; 

• 時間復雜度：
• 空間復雜度：

當然我不建議這么寫，能寫出版本一就可以了，直觀簡潔!

在后序的講解中，可能我會忽略這種版本二的寫法，大家只要知道有這么個寫法就可以了哈。

拓展

這道題描述也確實有點魔幻。

題目描述為：每當你爬上一個階梯你都要花費對應的體力值，一旦支付了相應的體力值，你就可以選擇向上爬一個階梯或者爬兩個階梯。

示例1：

輸入：cost = [10, 15, 20] 輸出：15

從題目描述可以看出：要不是第一步不需要花費體力，要不就是第最后一步不需要花費體力，我個人理解：題意說的其實是第一步是要支付費用的!。因為是當你爬上一個臺階就要花費對應的體力值!

所以我定義的dp[i]意思是也是第一步是要花費體力的，最后一步不用花費體力了，因為已經支付了。

當然也可以樣，定義dp[i]為:第一步是不花費體力，最后一步是花費體力的。

所以代碼這么寫：

class Solution { 
public: 
    int minCostClimbingStairs(vector<int>& cost) { 
        vector<int> dp(cost.size() + 1); 
        dp[0] = 0; // 默認第一步都是不花費體力的 
        dp[1] = 0; 
        for (int i = 2; i <= cost.size(); i++) { 
            dp[i] = min(dp[i - 1] + cost[i - 1], dp[i - 2] + cost[i - 2]); 
        } 
        return dp[cost.size()]; 
    } 
}; 

這么寫看上去比較順，但是就是感覺和題目描述的不太符。哈哈，也沒有必要這么細扣題意了，大家只要知道，題目的意思反正就是要不是第一步不花費，要不是最后一步不花費，都可以。

總結

大家可以發現這道題目相對于 昨天的動態規劃：爬樓梯有難了一點，但整體思路是一樣。

從動態規劃：斐波那契數到 動態規劃：爬樓梯再到今天這道題目，錄友們感受到循序漸進的梯度了嘛。

每個系列開始的時候，都有錄友和我反饋說題目太簡單了，趕緊上難度，但也有錄友和我說有點難了，快跟不上了。

其實我選的題目都是有目的性的，就算是簡單題，也是為了練習方法論，然后難度都是梯度上來的，一環扣一環。

但我也可以隨便選來一道難題講唄，這其實是最省事的，不用管什么題目順序，看心情找一道就講。

難的是把題目按梯度排好，循序漸進，再按照統一方法論把這些都串起來，哈哈，所以大家不要催我哈，按照我的節奏一步一步來就行啦。

學算法，認準「代碼隨想錄」，沒毛病!

其他語言版本

Java

class Solution { 
    public int minCostClimbingStairs(int[] cost) { 
        if (cost == null || cost.length == 0) { 
            return 0; 
        } 
        if (cost.length == 1) { 
            return cost[0]; 
        } 
        int[] dp = new int[cost.length]; 
        dp[0] = cost[0]; 
        dp[1] = cost[1]; 
        for (int i = 2; i < cost.length; i++) { 
            dp[i] = Math.min(dp[i - 1], dp[i - 2]) + cost[i]; 
        } 
        //最后一步，如果是由倒數第二步爬，則最后一步的體力花費可以不用算 
        return Math.min(dp[cost.length - 1], dp[cost.length - 2]); 
    } 
} 

Python

class Solution: 
    def minCostClimbingStairs(self, cost: List[int]) -> int: 
        dp = [0] * (len(cost)) 
        dp[0] = cost[0] 
        dp[1] = cost[1] 
        for i in range(2, len(cost)): 
            dp[i] = min(dp[i - 1], dp[i - 2]) + cost[i] 
        return min(dp[len(cost) - 1], dp[len(cost) - 2]) 

Go

func minCostClimbingStairs(cost []int) int { 
 dp := make([]int, len(cost)) 
 dp[0], dp[1] = cost[0], cost[1] 
 for i := 2; i < len(cost); i++ { 
  dp[i] = min(dp[i-1], dp[i-2]) + cost[i] 
 } 
 return min(dp[len(cost)-1], dp[len(cost)-2]) 
} 
 
func min(a, b int) int { 
 if a < b { 
  return a 
 } 
 return b 
} 

 Javascript

var minCostClimbingStairs = function(cost) { 
    const dp = [ cost[0], cost[1] ] 
 
    for (let i = 2; i < cost.length; ++i) { 
        dp[i] = Math.min(dp[i -1] + cost[i], dp[i - 2] + cost[i]) 
    } 
 
    return Math.min(dp[cost.length - 1], dp[cost.length - 2]) 
};