[[441765]]

大家好，我是bigsai，好久不見，天天想念。

最近不少小伙伴跟我交流刷題腫么刷，我給的建議就是先劍指offer和力扣hot100，在這些題中還有些重要程度和出現(xiàn)頻率是非常非常高的，今天給大家分享當今出現(xiàn)頻率最高的10道算法題，最近鋪天蓋地的出現(xiàn)，學到就是賺到。

本篇主要內容為：

0X01翻轉鏈表

力扣206和劍指offer24原題，題意為：

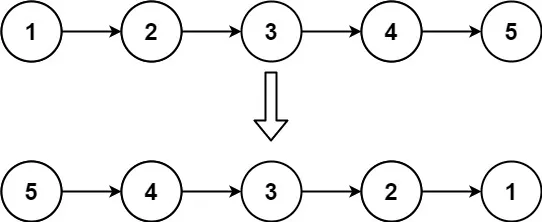
給你單鏈表的頭節(jié)點 head ，請你反轉鏈表，并返回反轉后的鏈表。

分析：

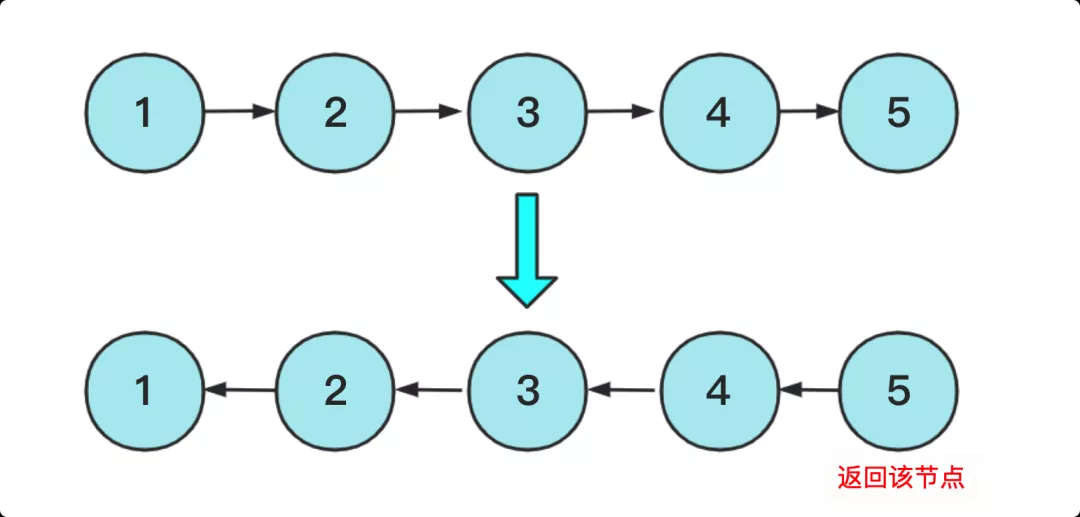
翻轉鏈表，本意是不創(chuàng)建新的鏈表節(jié)點然后在原鏈表上實現(xiàn)翻轉，但是這個圖有點會誤導人的思維，其實更好的理解你可以看下面這幅圖：

具體實現(xiàn)上兩個思路，非遞歸和遞歸的實現(xiàn)方式，非遞歸的實現(xiàn)方式比較簡單，利用一個pre節(jié)點記錄前驅節(jié)點，向下枚舉的時候改變指針指向就可以，實現(xiàn)代碼為：

class Solution { 
    public ListNode reverseList(ListNode head) { 
       if(head==null||head.next==null)//如果節(jié)點為NULL或者單個節(jié)點直接返回 
            return head; 
        ListNode pre=head;//前驅節(jié)點 
        ListNode cur=head.next;//當前節(jié)點用來枚舉 
        while (cur!=null) 
        { 
            ListNode next=cur.next; 
            //改變指向 
            cur.next=pre; 
            pre=cur; 
            cur=next; 
        } 
        head.next=null;//將原先的head節(jié)點next置null防止最后成環(huán) 
        return pre; 
    } 
} 

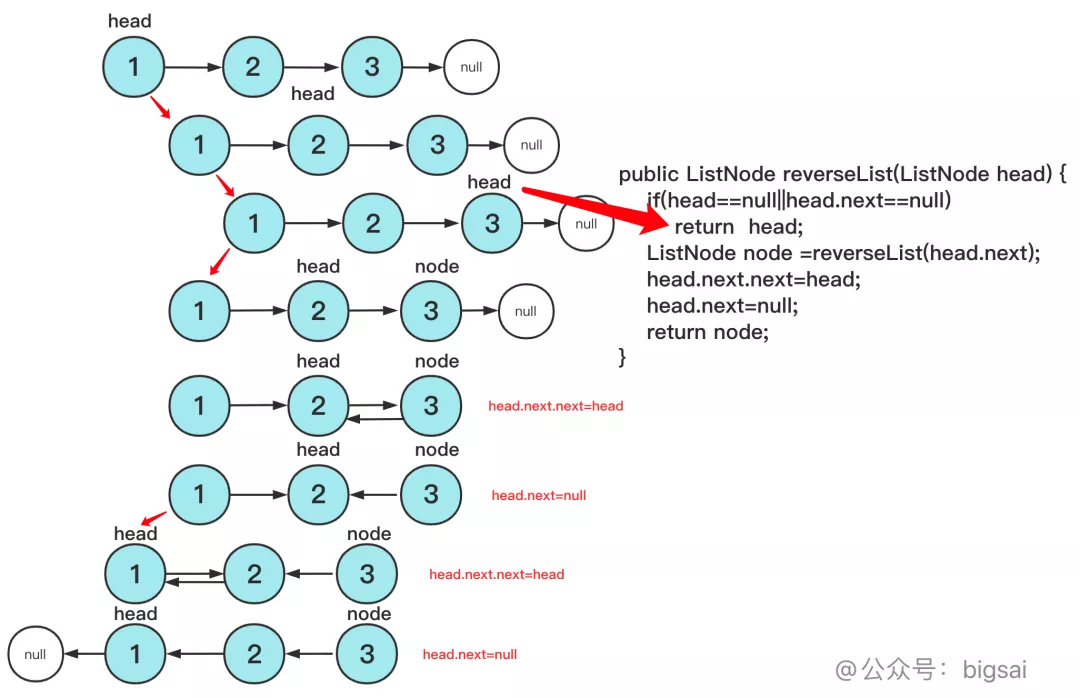
而遞歸的方式比較巧妙，借助遞歸歸來的過程巧妙改變指針指向和返回值傳遞，代碼雖然精簡但是理解起來有一定難度的，這里用一張圖幫助大家理解：

具體代碼為：

class Solution { 
    public ListNode reverseList(ListNode head) { 
        if(head==null||head.next==null)//如果最后一個節(jié)點不操作 
            return  head; 
        ListNode node =reverseList(head.next);//先遞歸 到最底層 然后返回 
        head.next.next=head;//后面一個節(jié)點指向自己 
        head.next=null;//自己本來指向的next置為null 
        return node;//返回最后一個節(jié)點(一直被遞歸傳遞) 
    } 
} 

0X02設計LRU

對應力扣146LRU緩存機制,題目要求為：

運用你所掌握的數(shù)據(jù)結構，設計和實現(xiàn)一個 LRU 緩存機制 。實現(xiàn) LRUCache 類：

LRUCache(int capacity) 以正整數(shù)作為容量 capacity 初始化 LRU 緩存

int get(int key) 如果關鍵字 key 存在于緩存中，則返回關鍵字的值，否則返回 -1 。

void put(int key, int value) 如果關鍵字已經(jīng)存在，則變更其數(shù)據(jù)值;如果關鍵字不存在，則插入該組「關鍵字-值」。當緩存容量達到上限時，它應該在寫入新數(shù)據(jù)之前刪除最久未使用的數(shù)據(jù)值，從而為新的數(shù)據(jù)值留出空間。

進階：在 O(1) 時間復雜度內完成這兩種操作

詳細分析：一次倒在LRU上的經(jīng)歷

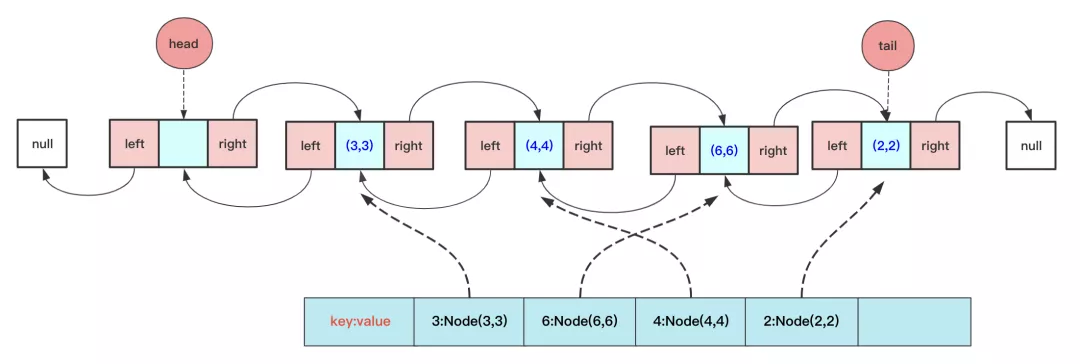
LRU的核心就是借助哈希+雙鏈表，哈希用于查詢，雙鏈表實現(xiàn)刪除只知道當前節(jié)點也能O(1)的復雜度刪除，不過雙鏈表需要考慮的頭尾指針特殊情況。

具體實現(xiàn)的代碼為：

class LRUCache { 
    class Node { 
        int key; 
        int value; 
        Node pre; 
        Node next; 
        public Node() { 
        } 
        public Node( int key,int value) { 
            this.key = key; 
            this.value=value; 
        } 
    } 
    class DoubleList{ 
        private Node head;// 頭節(jié)點 
        private Node tail;// 尾節(jié)點 
        private int length; 
        public DoubleList() { 
            head = new Node(-1,-1); 
            tail = head; 
            length = 0; 
        } 
        void add(Node teamNode)// 默認尾節(jié)點插入 
        { 
            tail.next = teamNode; 
            teamNode.pre=tail; 
            tail = teamNode; 
            length++; 
        } 
        void deleteFirst(){ 
            if(head.next==null) 
                return; 
            if(head.next==tail)//如果刪除的那個剛好是tail  注意啦 tail指針前面移動 
                tail=head; 
            head.next=head.next.next; 
 
            if(head.next!=null) 
                head.next.pre=head; 
            length--; 
        } 
        void deleteNode(Node team){ 
 
            team.pre.next=team.next; 
            if(team.next!=null) 
                team.next.pre=team.pre; 
            if(team==tail) 
                tail=tail.pre; 
           team.pre=null; 
           team.next=null; 
            length--; 
        } 
    } 
    Map<Integer,Node> map=new HashMap<>(); 
    DoubleList doubleList;//存儲順序 
    int maxSize; 
    LinkedList<Integer>list2=new LinkedList<>(); 
 
    public   LRUCache(int capacity) { 
        doubleList=new DoubleList(); 
        maxSize=capacity; 
    } 
    public int get(int key) { 
        int val; 
        if(!map.containsKey(key)) 
            return  -1; 
        val=map.get(key).value; 
        Node team=map.get(key); 
        doubleList.deleteNode(team); 
        doubleList.add(team); 
        return  val; 
    } 
 
    public void put(int key, int value) { 
        if(map.containsKey(key)){// 已經(jīng)有這個key 不考慮長短直接刪除然后更新 
           Node deleteNode=map.get(key); 
            doubleList.deleteNode(deleteNode); 
        } 
        else if(doubleList.length==maxSize){//不包含并且長度小于 
            Node first=doubleList.head.next; 
            map.remove(first.key); 
            doubleList.deleteFirst(); 
        } 
       Node node=new Node(key,value); 
        doubleList.add(node); 
        map.put(key,node); 
 
    } 
} 

0X03環(huán)形鏈表

對應力扣141和力扣142，力扣141環(huán)形鏈表要求為：

給定一個鏈表，判斷鏈表中是否有環(huán)，用O(1)內存解決。

詳細分析：環(huán)形鏈表找入口，真的太妙了

這個問題利用快慢雙指針比較高效，快指針fast每次走2步，slow每次走1步，慢指針走n步到尾時候快指針走了2n步，而環(huán)的大小一定小于等于n所以一定會相遇，如果相遇那么說明有環(huán)，如果不相遇fast先為null說明無環(huán)。

具體代碼為：

public class Solution { 
    public boolean hasCycle(ListNode head) { 
        ListNode fast=head; 
        ListNode slow=fast; 
        while (fast!=null&&fast.next!=null) { 
            slow=slow.next; 
            fast=fast.next.next; 
            if(fast==slow) 
                return true; 
        } 
        return false;     
    } 
} 

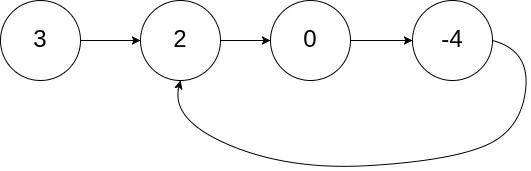
力扣142是在力扣141拓展，如有有環(huán)，返回入環(huán)的那個節(jié)點，就想下圖環(huán)形鏈表返回節(jié)點2。

 

這個問題是需要數(shù)學轉換的，具體的分析可以看上面的詳細分析，這里面提一下大題的步驟。

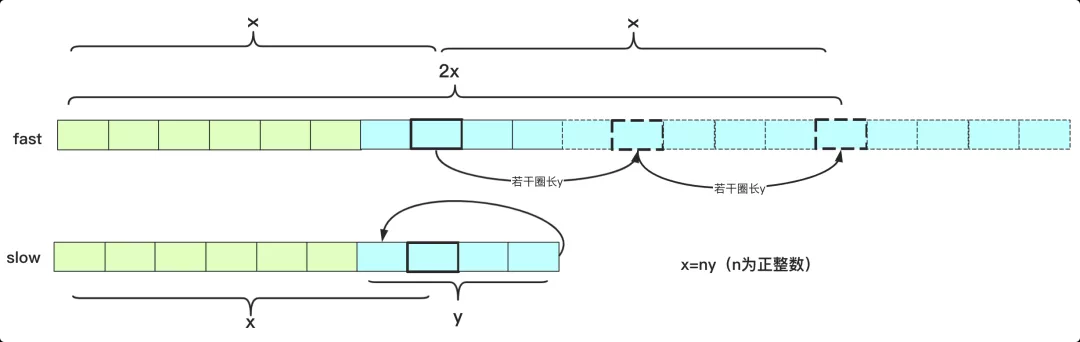
如果找到第一個交匯點，其中一個停止，另一個繼續(xù)走，下一次交匯時候剛好走一圈，可以算出循環(huán)部分長度為y。

所以我們知道的東西有：交匯時候fast走2x步，slow走x步，環(huán)長為y。并且快指針和慢指針交匯時候，多走的步數(shù)剛好是換長y的整數(shù)倍(它兩此刻在同一個位置，快指針剛好多繞整數(shù)倍圈數(shù)才能在同一個位置相聚)，可以得到2x=x+ny(x=ny)。其中所以說慢指針走的x和快指針多走的x是圈長y的整數(shù)倍。

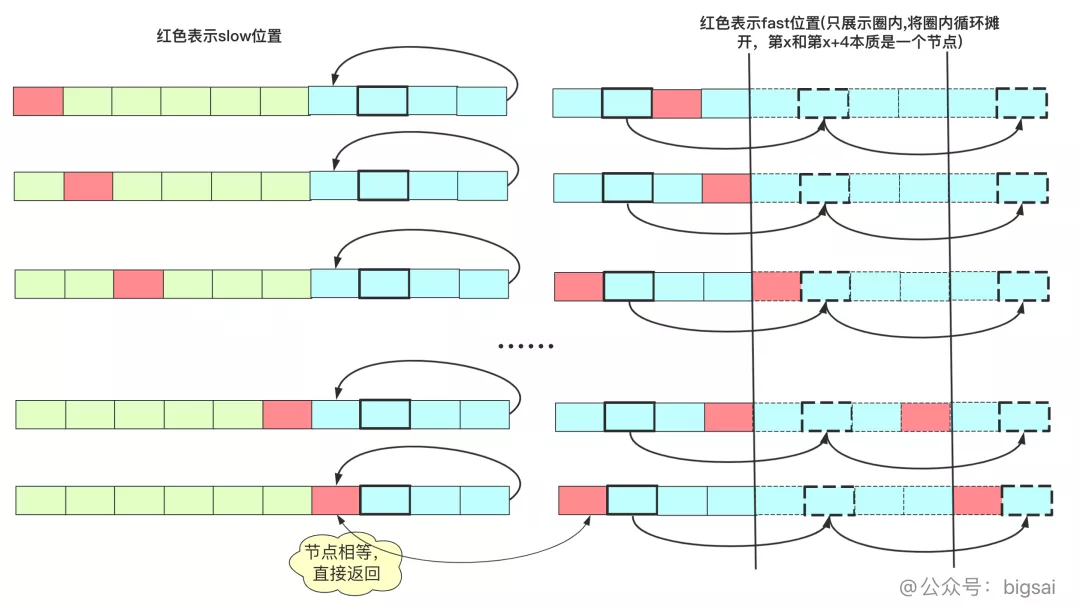
也就是說，從開頭走到這個點共計x步，從這個點走x步也就是繞了幾圈也回到這個點。如果說slow從起點出發(fā)，fast從這個點出發(fā)(每次走一步，相當于之前兩步抵消slow走的路程)，那么走x步還會到達這個點，但是這兩個指針這次都是每次走一步，所以一旦slow到達循環(huán)圈內，兩個指針就開始匯合了。

實現(xiàn)代碼為：

public class Solution { 
    public ListNode detectCycle(ListNode head) { 
        boolean isloop=false; 
        ListNode fast=new ListNode(0);//頭指針 
        ListNode slow=fast; 
        fast.next=head; 
        if(fast.next==null||fast.next.next==null) 
            return null; 
        while (fast!=null&&fast.next!=null) { 
            fast=fast.next.next; 
            slow=slow.next; 
            if(fast==slow) 
            { 
                isloop=true; 
                break; 
            } 
        } 
        if(!isloop)//如果沒有環(huán)返回 
            return null; 
        ListNode team=new ListNode(-1);//頭指針 下一個才是head 
        team.next=head; 
        while (team!=fast) {//slow 和fast 分別從起點和當前點出發(fā) 
            team=team.next; 
            fast=fast.next; 
        } 
        return team; 
    } 
} 

0X04兩個棧實現(xiàn)隊列對

應劍指offer09，題意為：

用兩個棧實現(xiàn)一個隊列。隊列的聲明如下，請實現(xiàn)它的兩個函數(shù) appendTail 和 deleteHead ，分別完成在隊列尾部插入整數(shù)和在隊列頭部刪除整數(shù)的功能。(若隊列中沒有元素，deleteHead 操作返回 -1 )

分析：

解決這個問題，要知道棧是什么，隊列是什么，兩種常見數(shù)據(jù)結構格式很簡單，棧的特點就是：后進先出，隊列的特點就是：先進先出，棧可以想象成一堆書本，越在上面的取的越早，上面來上面出(比喻一下);隊列就是想象成排隊買東西，只能后面進前面出，所以兩者數(shù)據(jù)結構還是有區(qū)別的，雖然都是單個入口進出，但是棧進出口相同，而隊列不同。

上面描述的是一個普通棧和隊列的數(shù)據(jù)結構，這里面讓我們用兩個棧實現(xiàn)一個隊列的操作，這里比較容易想的方案就是其中一個棧stack1用作數(shù)據(jù)存儲，插入尾時候直接插入stack1，而刪除頭的時候將數(shù)據(jù)先加入到另一個棧stack2中，返回并刪除棧頂元素，將stack2順序加入stack1中實現(xiàn)一個復原，但是這樣操作插入時間復雜度為O(1),刪除時間復雜度為O(n)比較高。

實現(xiàn)方式也給大家看下：

class CQueue { 
 
    Stack<Integer>stack1=new Stack<>(); 
    Stack<Integer>stack2=new Stack<>(); 
    public CQueue() { 
    } 
    public void appendTail(int value) { 
       stack1.push(value); 
    } 
    public int deleteHead() { 
        if(stack1.isEmpty()) 
            return -1; 
 
        while (!stack1.isEmpty()) 
        { 
            stack2.push(stack1.pop()); 
        } 
       int value= stack2.pop(); 
        while (!stack2.isEmpty()) 
        { 
            stack1.push(stack2.pop()); 
        } 
        return  value; 
    } 
} 

這樣的時間復雜度是不被喜歡的，因為刪除太雞兒耗時了，每次都要折騰一番，有沒有什么好的方法能夠讓刪除也方便一點呢?

有啊，stack1可以順序保證順序插入，stack1數(shù)據(jù)放到stack2中可以保證順序刪除，所以用stack1作插入，stack2作刪除，因為題目也沒要求數(shù)據(jù)必須放到一個容器中，所以就這樣組合使用，完美perfect!

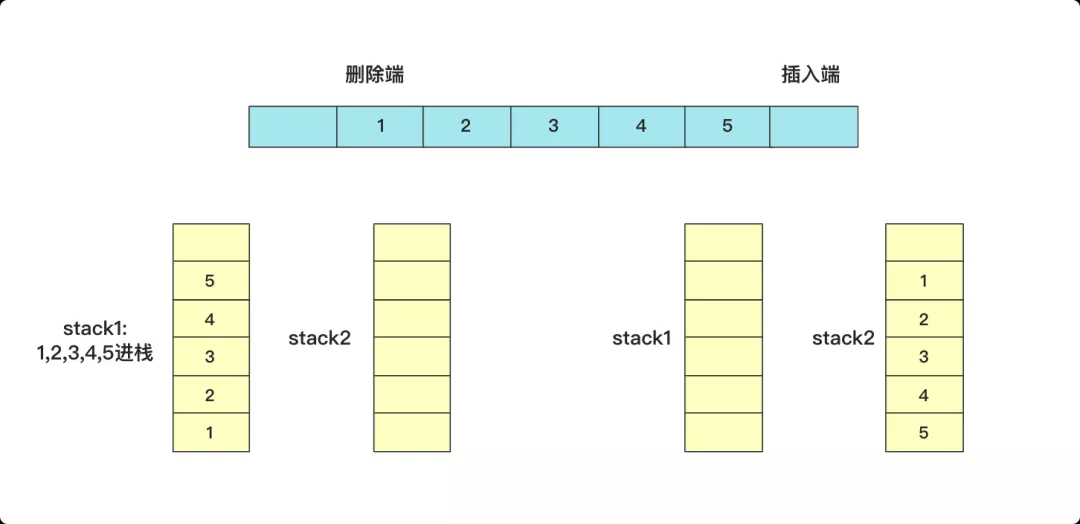
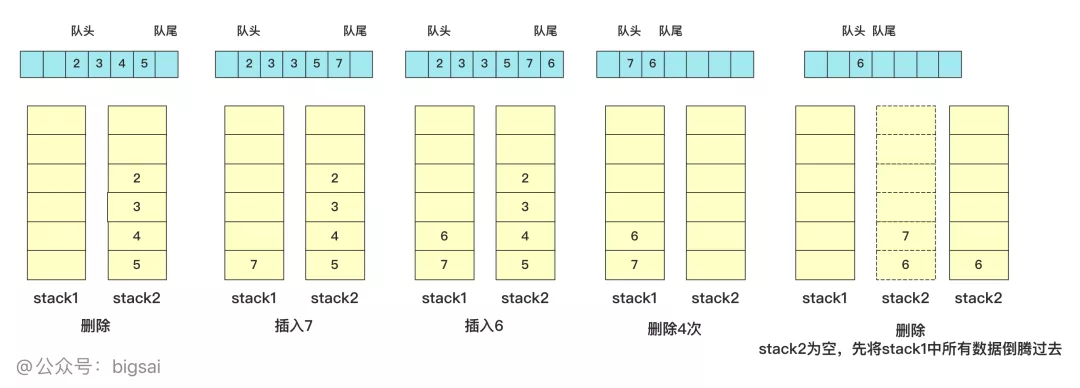
具體實現(xiàn)的時候，插入直接插入到stack1中，如果需要刪除從stack2中棧頂刪除，如果stack2棧為空那么將stack1中數(shù)據(jù)全部添加進來(這樣又能保證stack2中所有數(shù)據(jù)是可以順序刪除的了)，下面列舉幾個刪除的例子

其實就是將數(shù)據(jù)分成兩個部分，一部分用來插入，一部分用來刪除，刪除的那個棧stack2空了添加所有stack1中的數(shù)據(jù)繼續(xù)操作。這個操作插入刪除的時間復雜度是O(1),具體實現(xiàn)的代碼為：

class CQueue { 
    Deque<Integer> stack1; 
    Deque<Integer> stack2; 
 
    public CQueue() { 
        stack1 = new LinkedList<Integer>(); 
        stack2 = new LinkedList<Integer>(); 
    } 
 
    public void appendTail(int value) { 
        stack1.push(value); 
    } 
 
    public int deleteHead() { 
        // 如果第二個棧為空 將stack1數(shù)據(jù)加入stack2 
        if (stack2.isEmpty()) { 
            while (!stack1.isEmpty()) { 
                stack2.push(stack1.pop()); 
            } 
        } //如果stack2依然為空 說明沒有數(shù)據(jù) 
        if (stack2.isEmpty()) { 
            return -1; 
        } else {//否則刪除 
            int deleteItem = stack2.pop(); 
            return deleteItem; 
        } 
    } 
} 

0X05二叉樹層序(鋸齒)遍歷

二叉樹的遍歷，對應力扣102，107，103.

詳細分析：一次面試，被二叉樹層序遍歷打爆了

如果普通二叉樹層序遍歷，也不是什么困難的問題，但是它會有個分層返回結果的操作，就需要你詳細考慮了。

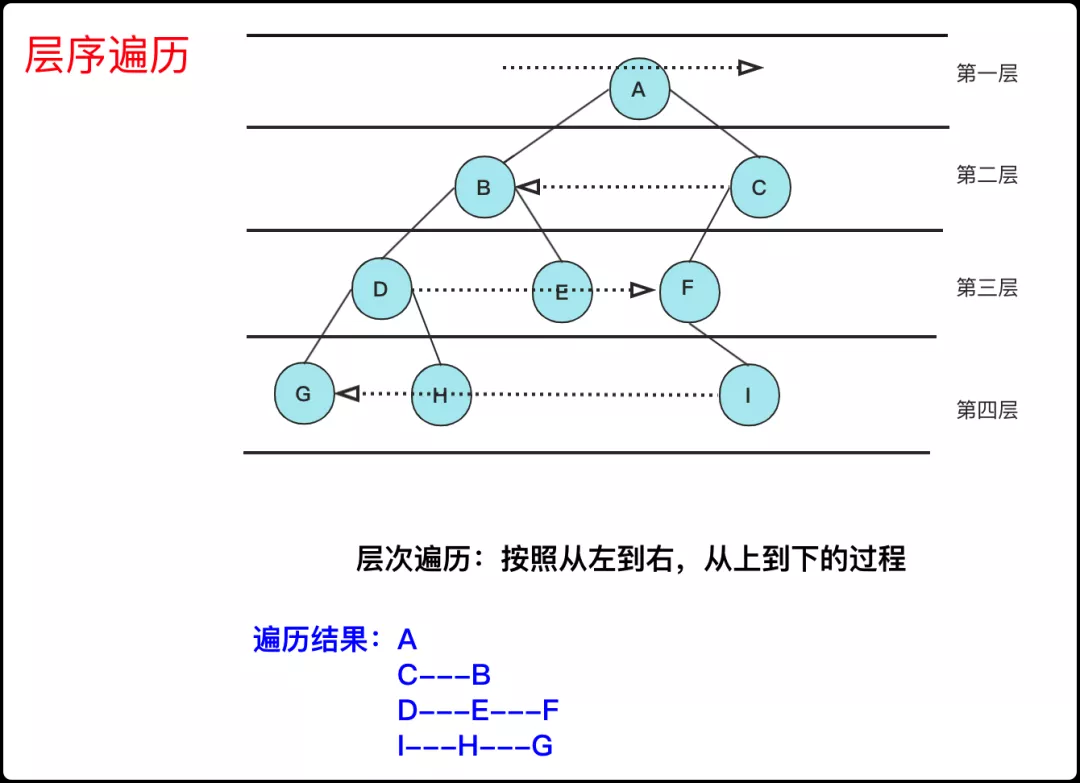
很多人會用兩個容器(隊列)進行分層的操作，這里其實可以直接使用一個隊列，我們首先記錄枚舉前隊列大小len，然后根據(jù)這個大小len去枚舉遍歷就可以得到完整的該層數(shù)據(jù)了。

還有一個難點就是二叉樹的鋸齒層序(也叫之字形打印)，第一趟是從左往右，第二趟是從右往左，只需要記錄一個奇偶層數(shù)進行對應的操作就可以了。

這里就拿力扣103二叉樹的鋸齒形層序遍歷作為題板給大家分享一下代碼：

public List<List<Integer>> levelOrder(TreeNode root) { 
  List<List<Integer>> value=new ArrayList<>();//存儲到的最終結果 
  if(root==null) 
    return value; 
  int index=0;//判斷 
  Queue<TreeNode>queue=new ArrayDeque<>(); 
  queue.add(root); 
  while (!queue.isEmpty()){ 
    List<Integer>va=new ArrayList<>();//臨時 用于存儲到value中 
    int len=queue.size();//當前層節(jié)點的數(shù)量 
    for(int i=0;i<len;i++){ 
      TreeNode node=queue.poll(); 
      if(index%2==0)//根據(jù)奇偶 選擇添加策略 
        va.add(node.val); 
      else 
        va.add(0,node.val); 
      if(node.left!=null) 
        queue.add(node.left); 
      if(node.right!=null) 
        queue.add(node.right); 
    } 
    value.add(va); 
    index++; 
  } 
  return value; 
} 

0X06 二叉樹中后序遍歷(非遞歸)

二叉樹的非遞歸遍歷也是考察的重點，對于中序后序遍歷遞歸實現(xiàn)很簡單，非遞歸實現(xiàn)起來還是要點技巧的哦。

詳細分析：二叉樹的各種遍歷(遞歸、非遞歸)

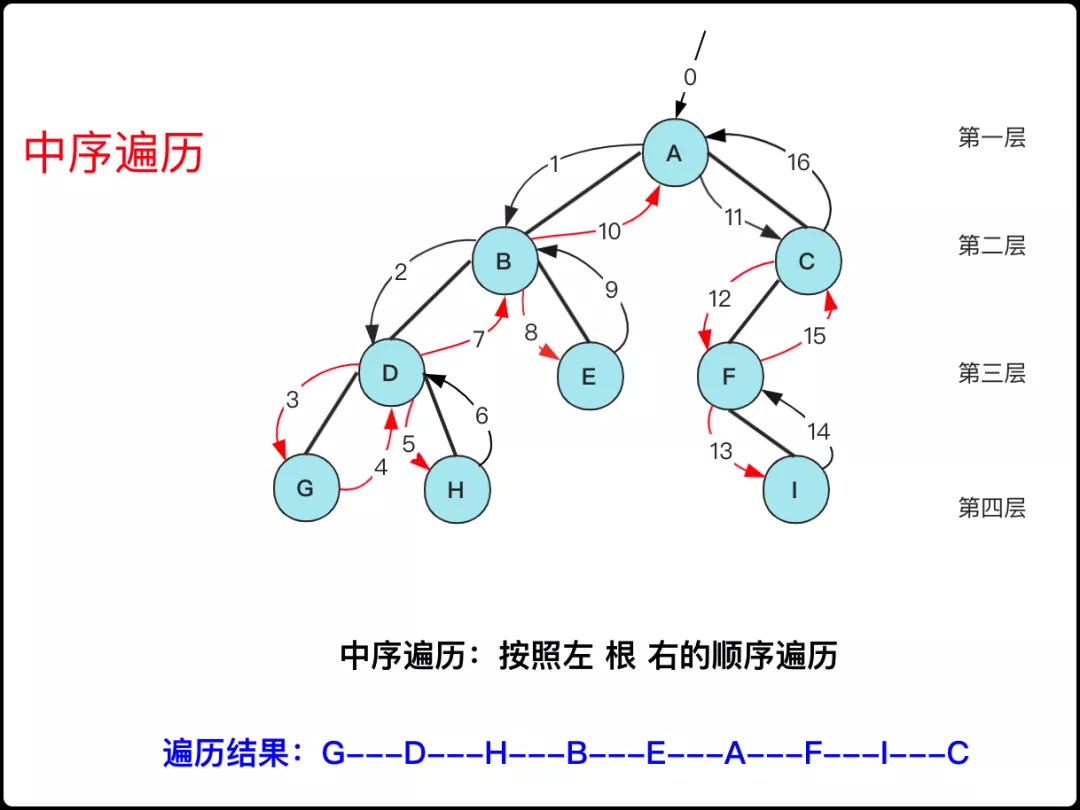
對于二叉樹的中序遍歷，其實就是正常情況第二次訪問該節(jié)點的時候才拋出輸出(第一次數(shù)前序)，這樣我們枚舉每個節(jié)點第一次不能刪除，需要先將它存到棧中，當左子節(jié)點處理完成的時候在拋出訪問該節(jié)點。

 

核心也就兩步，葉子節(jié)點左右都為null，也可滿足下列條件：

枚舉當前節(jié)點(不存儲輸出)并用棧存儲，節(jié)點指向左節(jié)點，直到左孩子為null。

拋出棧頂訪問。如果有右節(jié)點，訪問其右節(jié)點重復步驟1，如有沒右節(jié)點，繼續(xù)重復步驟2拋出。

實現(xiàn)代碼為：

class Solution { 
   public List<Integer> inorderTraversal(TreeNode root) { 
    List<Integer>value=new ArrayList<Integer>(); 
    Stack<TreeNode> q1 = new Stack();     
    while(!q1.isEmpty()||root!=null) 
    { 
        while (root!=null) { 
            q1.push(root);                 
            root=root.left; 
        } 
        root=q1.pop();//拋出 
        value.add(root.val); 
        root=root.right;//準備訪問其右節(jié)點 
 
    } 
    return value; 
  } 
} 

而后序遍歷按照遞歸的思路其實一般是第三次訪問該節(jié)點是從右子節(jié)點回來才拋出輸出，這個實現(xiàn)起來確實有難度。但是具體的實現(xiàn)，我們使用一個pre節(jié)點記錄上一次被拋出訪問的點，如果當前被拋出的右孩子是pre或者當前節(jié)點右為null，那么就將這個點拋出，否則說明它的右側還未被訪問需要將它"回爐重造"，后面再用!如果不理解可以看前面的詳細介紹。

具體實現(xiàn)的代碼為：

class Solution { 
    public List<Integer> postorderTraversal(TreeNode root) { 
        TreeNode temp=root;//枚舉的臨時節(jié)點 
        List<Integer>value=new ArrayList<>(); 
        TreeNode pre=null;//前置節(jié)點 
        Stack<TreeNode>stack=new Stack<>(); 
 
        while (!stack.isEmpty()||temp!=null){ 
 
            while(temp!=null){ 
                stack.push(temp); 
                temp=temp.left; 
            } 
            temp=stack.pop(); 
            if(temp.right==pre||temp.right==null)//需要彈出 
            { 
                value.add(temp.val); 
                pre=temp; 
                temp=null;//需要重新從棧中拋出 
            }else{ 
                stack.push(temp); 
                temp=temp.right; 
            } 
 
        } 
        return value; 
    } 
} 

當然，后序遍歷也有用前序(根右左)的前序遍歷結果最后翻轉一下的，但面試官更想考察的還是上面提到的方法。

0X07 跳臺階(斐波那契、爬樓梯)

爬樓梯、跳臺階是一個經(jīng)典問題，對應劍指offer10和力扣70題，題目的要求為：

假設你正在爬樓梯。需要 n 階你才能到達樓頂。每次你可以爬 1 或 2 個臺階。你有多少種不同的方法可以爬到樓頂呢?注意：給定 n 是一個正整數(shù)。

分析：

這個問題入門級別dp，分析當前第k階的結果，每個人可以爬1個或者2個臺階，那么說明它可能是由k-1或者k-2來的，所以就是兩個子情況的疊加(需要特殊考慮一下初始情況)，這個思路有人會想到遞歸，沒錯用遞歸確實可以解決但是用遞歸效率較低(因為這個是個發(fā)散的遞歸一個拆成兩個)，使用記憶化搜索會稍微好一些。

但是dp是比較好的方法，核心狀態(tài)轉移方程為：dp[i]=dp[i-1]+dp[i-2]，有些空間優(yōu)化的那就更好了，因為只用到前兩個值，所以完全可以用三個值重復使用節(jié)省空間。

class Solution { 
    public int climbStairs(int n) { 
        if(n<3)return n; 
         int dp[]=new int[n+1]; 
         dp[1]=1; 
         dp[2]=2; 
         for(int i=3;i<n+1;i++) 
         { 
             dp[i]=dp[i-1]+dp[i-2]; 
         } 
         return dp[n]; 
    } 
 
  public int climbStairs(int n) { 
        int a = 0, b = 0, c = 1; 
        for (int i = 1; i <= n; i++) { 
            a = b;  
            b = c;  
            c = a + b; 
        } 
        return c; 
    } 
} 

當然，有的數(shù)據(jù)很大求余的跳臺階，可以用矩陣快速冪解決，但是這里就不介紹啦，有興趣可以詳細看看。

0X08 TOPK問題

TOPK問題真的非常經(jīng)典，通常問的有最小的K個數(shù)，尋找第K大都是TOPK這種問題，這里就用力扣215尋找數(shù)組第K大元素作為板子。

詳細分析：一文拿捏TOPK

TOPK的問題解決思路有很多，如果優(yōu)化的冒泡或者簡單選擇排序，時間復雜度為O(nk),使用優(yōu)化的堆排序為O(n+klogn)，不過掌握快排的變形就可以應付大體上的所有問題了(面試官要是讓你手寫堆排序那真是有點難為你了)。

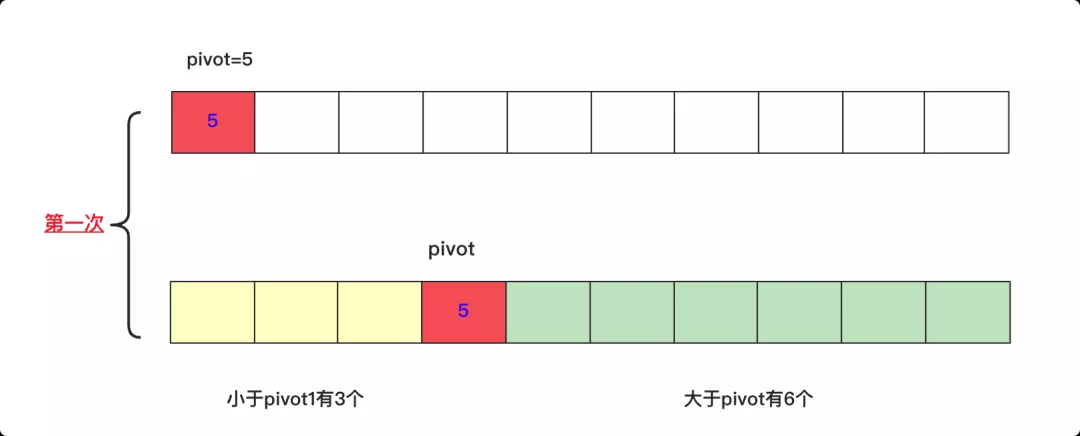
快排每次確定一個數(shù)pivot位置，將數(shù)分成兩部分：左面的都比這個數(shù)pivot小，右面的都比這個數(shù)pivot大，這樣就可以根據(jù)這個k去判斷剛好在pivot位置，還是左側還是右側?可以壓縮空間迭代去調用遞歸最終求出結果。

很多人為了更快過測試樣例將這個pivot不選第一個隨機選擇(為了和刁鉆的測試樣例作斗爭)，不過這里我就選第一個作為pivot了，代碼可以參考：

class Solution { 
    public int findKthLargest(int[] nums, int k) { 
        quickSort(nums,0,nums.length-1,k); 
        return nums[nums.length-k]; 
    } 
    private void quickSort(int[] nums,int start,int end,int k) { 
        if(start>end) 
            return; 
        int left=start; 
        int right=end; 
        int number=nums[start]; 
        while (left<right){ 
            while (number<=nums[right]&&left<right){ 
                right--; 
            } 
            nums[left]=nums[right]; 
            while (number>=nums[left]&&left<right){ 
                left++; 
            } 
            nums[right]=nums[left]; 
        } 
        nums[left]=number; 
        int num=end-left+1; 
        if(num==k)//找到k就終止 
            return; 
        if(num>k){ 
            quickSort(nums,left+1,end,k); 
        }else { 
            quickSort(nums,start,left-1,k-num); 
        } 
    } 
} 

0X09 無重復的最長子串(數(shù)組)

這個問題可能是個字符串也可能是數(shù)組，但是道理一致，無重復字符的最長子串和最長無重復子數(shù)組本質一致。

題目要求為：給定一個字符串，請你找出其中不含有重復字符的 最長子串 的長度。

分析：

此題就是給一個字符串讓你找出最長沒有重復的一個子串。要搞清子串和子序列的區(qū)別：

子串：是連續(xù)的，可以看成原串的一部分截取。

子序列：不一定是連續(xù)的，但是要保證各個元素之間相對位置不變。

那么我們如何處理呢?

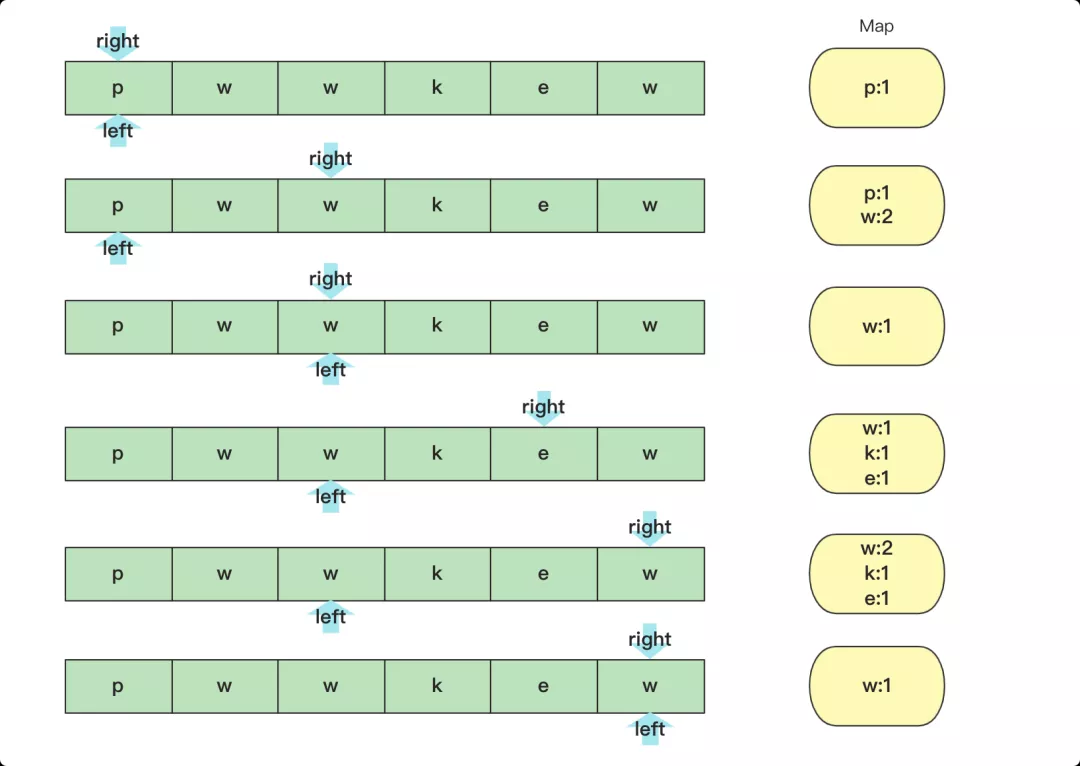
暴力查找，暴力查找當然是可以的，但是復雜度過高這里就不進行講解了。這里選擇的思路是滑動窗口，滑動窗口，就是用一個區(qū)間從左往右，右側先進行試探，找到區(qū)間無重復最大值，當有重復時左側再往右側移動一直到?jīng)]重復，然后重復進行到最后。在整個過程中找到最大子串即可。

具體實現(xiàn)時候可以用數(shù)組替代哈希表會快很多：

class Solution { 
    public int lengthOfLongestSubstring(String s) { 
         int a[]=new int[128]; 
         int max=0;//記錄最大 
         int l=0;//left 用i 當成right，當有重復左就往右 
         for(int i=0;i<s.length();i++) 
         { 
             a[s.charAt(i)]++; 
             while (a[s.charAt(i)]>1) { 
                a[s.charAt(l++)]--; 
            } 
             if(i-l+1>max) 
                 max=i-l+1; 
         } 
         return max; 
    } 
} 

0X10 排序

不會真的有人以為用個Arrays.sort()就完事了吧，手寫排序還是很高頻的，像冒泡、插入這些簡單的大家相比都會，像堆排序、希爾、基數(shù)排序等考察也不多，比較高頻的就是快排了，這里額外獎勵一個也很高頻的歸并排序，兩個都是典型分治算法，也可以將快排和前面的TOPK問題比較一番。

排序詳細的十大排序都有詳細講過，大家可以自行參考：程序員必知必會十大排序

快排：

具體實現(xiàn)：

public void quicksort(int [] a,int left,int right) 
{ 
  int low=left; 
  int high=right; 
  //下面兩句的順序一定不能混，否則會產生數(shù)組越界！！！very important！！！ 
  if(low>high)//作為判斷是否截止條件 
    return; 
  int k=a[low];//額外空間k，取最左側的一個作為衡量，最后要求左側都比它小，右側都比它大。 
  while(low<high)//這一輪要求把左側小于a[low],右側大于a[low]。 
  { 
    while(low<high&&a[high]>=k)//右側找到第一個小于k的停止 
    { 
      high--; 
    } 
    //這樣就找到第一個比它小的了 
    a[low]=a[high];//放到low位置 
    while(low<high&&a[low]<=k)//在low往右找到第一個大于k的，放到右側a[high]位置 
    { 
      low++; 
    } 
    a[high]=a[low];             
  } 
  a[low]=k;//賦值然后左右遞歸分治求之 
  quicksort(a, left, low-1); 
  quicksort(a, low+1, right);         
} 

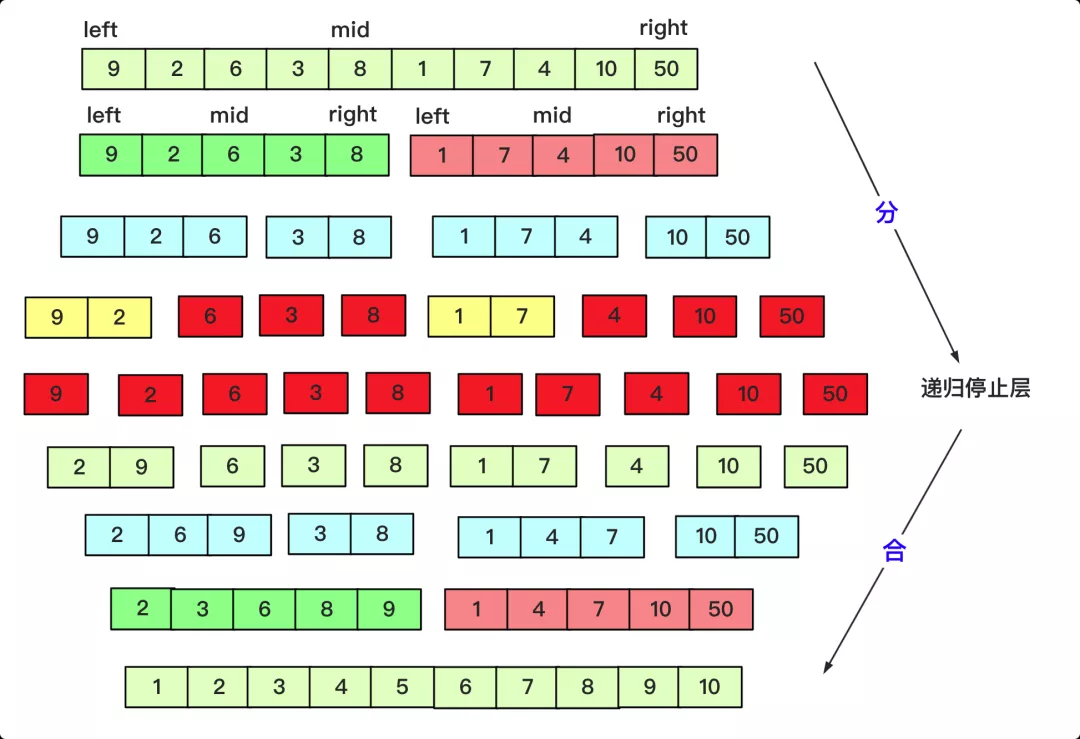
歸并排序:

實現(xiàn)代碼為：

private static void mergesort(int[] array, int left, int right) { 
  int mid=(left+right)/2; 
  if(left<right) 
  { 
    mergesort(array, left, mid); 
    mergesort(array, mid+1, right); 
    merge(array, left,mid, right); 
  } 
} 
 
private static void merge(int[] array, int l, int mid, int r) { 
  int lindex=l;int rindex=mid+1; 
  int team[]=new int[r-l+1]; 
  int teamindex=0; 
  while (lindex<=mid&&rindex<=r) {//先左右比較合并 
    if(array[lindex]<=array[rindex]) 
    { 
      team[teamindex++]=array[lindex++]; 
    } 
    else {                 
      team[teamindex++]=array[rindex++]; 
    } 
  } 
  while(lindex<=mid)//當一個越界后剩余按序列添加即可 
  { 
    team[teamindex++]=array[lindex++]; 
 
  } 
  while(rindex<=r) 
  { 
    team[teamindex++]=array[rindex++]; 
  }     
  for(int i=0;i<teamindex;i++) 
  { 
    array[l+i]=team[i]; 
  } 
} 

結語

好了，今天給大家分享的10個問題，是真的在面試中非常非常高頻，我敢說平均每兩次面試就得遇到這里面的其中一個題(毫不夸張)!

雖說題海很深學不完，但是學過緩存的都知道要把熱點數(shù)據(jù)放緩存，考過試的都知道要把必考點掌握……這十個問題已經(jīng)送到嘴邊。