用 TypeScript 實現斐波那契數列
前幾天在知乎看到一篇文章,用 TypeScript 類型運算實現一個中國象棋程序 :
邊看邊 woc,TypeScript 不是一個類型系統嗎,咋還實現象棋了,感覺發現了新大陸一樣,然后把大佬的代碼 clone下來,本地「運行」了一下,只能是帶引號的運行了,因為 TS就是動態推導類型,只需要安裝相關插件,鼠標 hover 上去就可以看到結果了。
看到這種神奇魔法,于是自己就查了查這是為什么。
圖靈完備
這是接觸到的第一個概念,維基百科是這樣定義的:
一個計算系統可以計算任何圖靈-可計算函數,被稱作圖靈完全(或者圖靈完備)。或者任何可以模擬通用圖靈機的系統。
可計算函數粗暴的理解為「人能計算的問題」,而現在例如 C++、JAVA幾乎所有編程語言都是具有圖靈完備性的,關于圖靈完備是一個更大的問題,更通俗的解釋可以看 什么是圖靈完備?知乎這篇回答,很有意思。
https://www.zhihu.com/question/20115374/answer/288346717
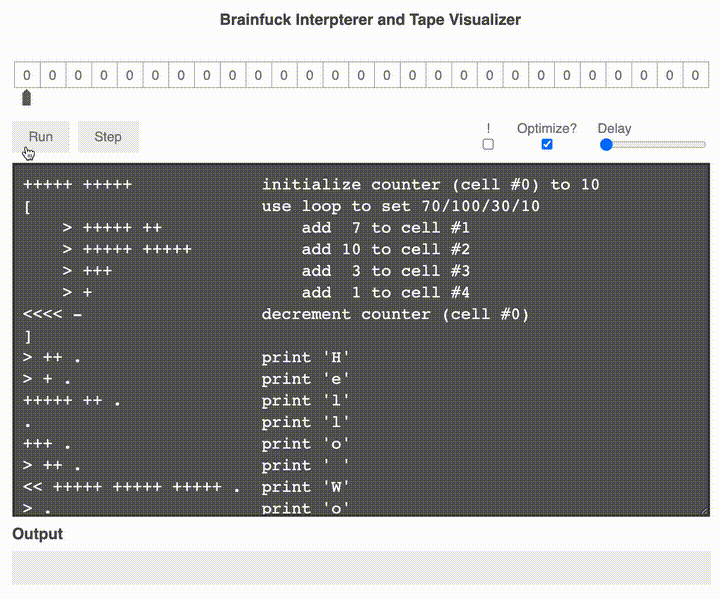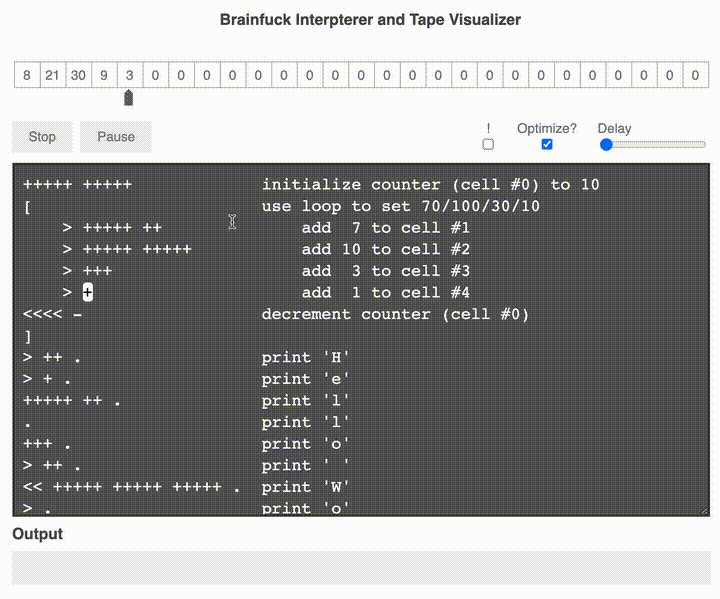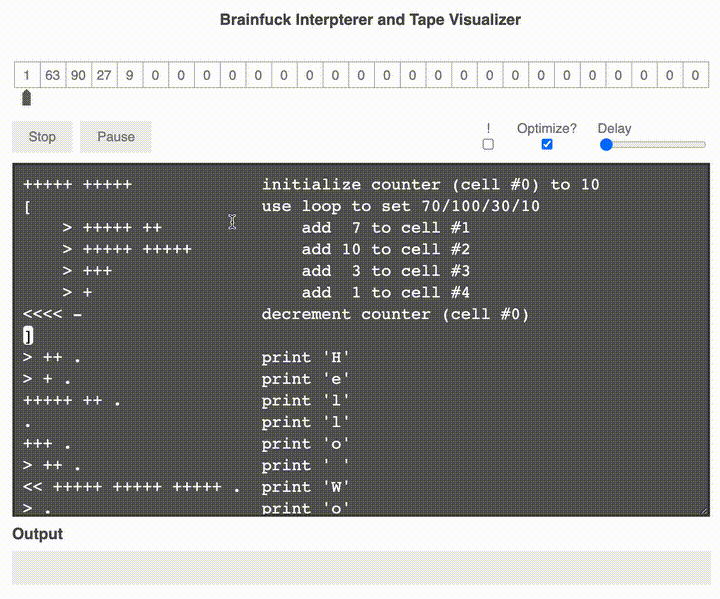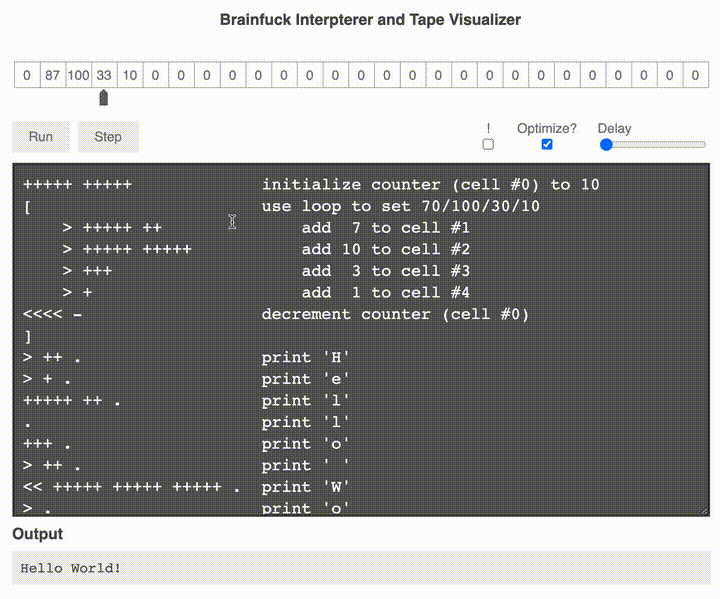
還了解到了一門有趣的編程語言 —— 1993 年Urban Müller 發明的Brainfuck 語言,感受一下它怎么打印 Hello World。
- +++++ +++++ initialize counter (cell #0) to 10
- [ use loop to set 70/100/30/10
- > +++++ ++ add 7 to cell #1
- > +++++ +++++ add 10 to cell #2
- > +++ add 3 to cell #3
- > + add 1 to cell #4
- <<<< - decrement counter (cell #0)
- ]
- > ++ . print 'H'
- > + . print 'e'
- +++++ ++ . print 'l'
- . print 'l'
- +++ . print 'o'
- > ++ . print ' '
- << +++++ +++++ +++++ . print 'W'
- > . print 'o'
是的,你沒有看錯,左邊是代碼,右邊是注釋,這里有運行的單句執行圖示,可以感受一下:
http://fatiherikli.github.io/brainfuck-visualizer/
上邊的紙帶代表內存中的情況,然后通過左移右移加加減減,最終輸出了 Hello world!。
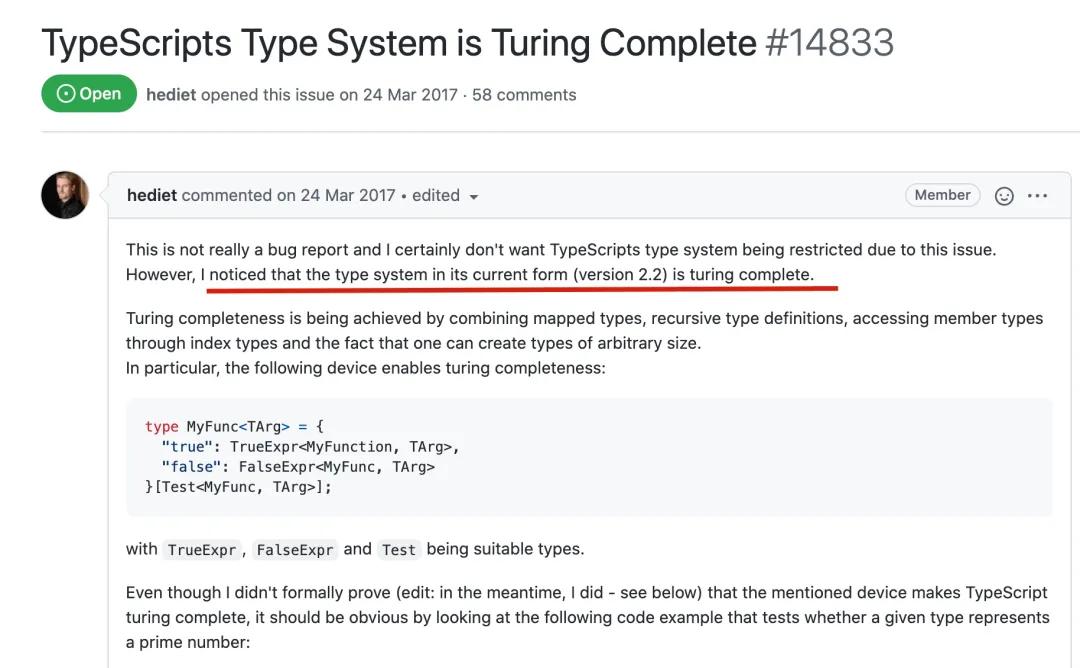
而在 TypeScript 倉庫的一個 issues 中也討論過 TypeScript 的圖靈完備了,作者還分享了一個判斷是否是質數的代碼,也很有意思。
TypeScript 相關知識
為了實現文章的標題 「用 TypeScript 實現斐波那契數列」,需要先學習下相關的知識點。
泛型
如果之前學過 C++ 或者 Java 之類的語言,對泛型一定不陌生,泛型可以讓我們定義函數參數的時候不指定參數類型,用一個占位符代替,當運行的時候再由外界傳過來的類型決定。
舉個簡單的例子,實現兩個元素相加,如果用 TypeScript 限制的話,即使是相同的邏輯也要寫多次了。
- function addTwoNumber(a: number, b: number):number {
- return a + b;
- }
- function addTwoNumberString(a: string, b: string):string {
- return a + b;
- }
- addTwoNumber(1,3)
- addTwoNumberString('1', '2');
不然的話就只能 anyScript 了,完全失去了類型校驗。
- function addTwoNumber(a: any, b: any):any {
- return a + b;
- }
- addTwoNumber(1,3)
- addTwoNumber('1', '2');
- addTwoNumber('1', 2); //不報錯
如果有泛型的話,就既可以達到邏輯的復用,同時對類型進行校驗。
- function addTwoNumber<T>(a: T, b: T): T {
- return <any>a + <any>b; //這里需要強制轉換下,不然會報 Operator '+' cannot be applied to types 'T' and 'T'.ts(2365)
- }
- addTwoNumber(1, 3);
- addTwoNumber("1", "3");
- addTwoNumber('1', 2); //報錯
當然上邊有強行用泛型的嫌疑了,不過能大體理解泛型的作用就好,哈哈。上邊的情況用 TS 的重載會更好些。
類型 type
TS 中除了基本的類型,number、string 、number[] 等,比較特殊的地方 1 、abc 、true 也可以單獨算一個類型。1 的類型是 1,當然也屬于 number。
最重要的是 TS 允許我們定義新的類型,而且我們還可以通過泛型變量,進行類型的運算然后產生新的類型。舉幾個例子:
- type Type1<T> = T extends number ? number : string;
- type Type2 = Type1<2121>; // 此時 Type2 就相當于 number
- type Type3 = Type1<{}>; // 此時 Type3 就相當于 string
exstends 和后邊的 ? 構成了一個三元表達式,如果 extends 前面的類型能夠賦值給 extends 后面的類型,那么表達式判斷為真,否則為假。
因為單個數字也是一個類型,所以我們就可以判斷傳入的 T 是否等于某個數。
- type Type4<T> = T extends 1 ? true : false;
- type Type5 = Type4<2121>; // 此時 Type5 就相當于 false 類型
- type Type6 = Type4<1>; // 此時 Type6 就相當于 true 類型
可以仔細體會一下這里,很關鍵,后邊寫斐波那契數列的時候,一不小心就會被繞進去,因為我們是在操控類型之間的運算,和平時的編程感覺很不一樣。
一句話總結,每個類型可以看成一個函數,傳入的泛型是函數參數,并且也是一個類型,最后再返回一個新的類型。
- Type(type, type) => type
infer
infer 表示在 extends 條件語句中待推斷的類型變量。
簡單理解,我們是為了判斷某個類型是否 extends 某個「結構」,但結構中參數的類型我們并不知道,此時我們寫一個 infer R(R只是占位,任何名字都可以),在類型推導的時候,R 就是當前類型真正的參數類型。舉個例子:
我們判斷 T 是否是 {a: XXX, b: XXX}的類型,因為 T 是泛型,我們并不知道T 中的 a 是什么類型,此時就可以用 infer 占位。當傳入具體的類型是就可以拿到 a 是什么類型了。
- type Foo<T> = T extends { a: infer U; b: infer U } ? U : never;
- type T1 = Foo<{ a: string; b: string }>; // T1 類型為 string
- type T2 = Foo<{ a: string; b: number }>; // T2 類型為 string | number
斐波那契數列
斐波那契數列就不多解釋了,先用 js 實現一個斐波那契數列。
- function Fibonacci(n) {
- if (n === 1) {
- return 1;
- }
- if (n === 2) {
- return 1;
- }
- return Fibonacci(n - 1) + Fibonacci(n - 2);
最關鍵的遞歸不用擔心,TS 支持類型的遞歸定義,我們先寫一個大概的雛形,看象棋直接用中文定義類型挺有意思,這里也直接中文了。之前總結的那句話這里再加深一下,每個類型可以看成一個函數,傳入的泛型是函數參數,并且也是一個類型,最后再返回一個新的類型。
我們先定義「斐波那契」類型,泛型是傳入一個數字(這里的數字是當作類型),先判斷傳入的類型是否是 1 或者 2,然后直接返回 1 類型。
- type 斐波那契<某數 extends number> = 某數 extends 1
- ? 1
- : 某數 extends 2
- ? 1
- : 相加<斐波那契<減一<某數>>, 斐波那契<減一<減一<某數>>>>;
: 相加<斐波那契<減一<某數>>, 斐波那契<減一<減一<某數>>>>;
上邊需要注意的是 <> 里邊的 extends 是為了限定傳入的類型,和外邊的 extends 不一樣。
我們還需要定義一個「相加」類型和一個「減一」類型。
相加是兩個類型相加,但是類型系統是不支持數字直接相加的,1 + 2 并不能直接相加,這里有個 trick。
數組類型和 js 中的數組一樣,同樣擁有 length 屬性,返回一個具體的數字類型,也支持擴展運算符。舉個例子:
- type A = [any, any, any]
- type B = A["length"] // B 就是 3 類型
所以我們可以將數字轉為數組,操作數組,然后再將數組通過 length 轉回數字。
先寫一個得到對應數組的 Type,這里就需要用到遞歸了。
- type 得到長度<數組 extends any[]> = 數組["length"];
- type 轉為數組<
- 某數 extends number,
- 對應數組 extends any[] = [] // 默認值賦一個空數組,外部調用的時候不需要傳
- > = 得到長度<對應數組> extends 某數 // 長度是否等于了需要的長度
- ? 對應數組 // 如果長度等于所需要的了就返回
- : 轉為數組<某數, [any, ...對應數組]>; // 否則再添加一個元素進入數組,然后遞歸調用
: 轉為數組<某數, [any, ...對應數組]>; // 否則再添加一個元素進入數組,然后遞歸調用
有了轉為數組的的 Type,相加方法就很好寫了,我們只需要將兩個數先轉為對應的數組,將兩個數組連接,最后返回連接后的數組長度即可。
- type 相加<某數甲 extends number, 某數乙 extends number> = 得到長度<
- [...轉為數組<某數甲>, ...轉為數組<某數乙>]
- >;
然后定義減一的方法,也就是數組長度減 1,這里就利用到了 infer,還需要利用數組的解構。
- type 數組減一<某數組類型 extends any[]> = ((
- ...參數: 某數組類型
- ) => any) extends (拆一個元素: any, ...剩下的數組: infer 剩下的數組類型) => any
- ? 剩下的數組類型
- : [];
我們定義了一個函數類型,通過函數參數的解構,使得剩下的數組少了一個元素。
有了「數組減一」的類型,數字「減一」就水到渠成了,將數字轉為對應數組,數組減去一個元素,然后恢復為數字即可。
- type 減一<某數 extends number> = 得到長度<數組減一<轉為數組<某數>>>;
整體代碼就出來了:
- type 斐波那契<某數 extends number> = 某數 extends 1
- ? 1
- : 某數 extends 2
- ? 1
- : 相加<斐波那契<減一<某數>>, 斐波那契<減一<減一<某數>>>>;
- type 得到長度<數組 extends any[]> = 數組["length"];
- type 轉為數組<
- 某數 extends number,
- 對應數組 extends any[] = []
- > = 得到長度<對應數組> extends 某數
- ? 對應數組
- : 轉為數組<某數, [any, ...對應數組]>;
- type 相加<某數甲 extends number, 某數乙 extends number> = 得到長度<
- [...轉為數組<某數甲>, ...轉為數組<某數乙>]
- >;
- type 數組減一<某數組類型 extends any[]> = ((
- ...參數: 某數組類型
- ) => any) extends (拆一個元素: any, ...剩下的數組: infer 剩下的數組類型) => any
- ? 剩下的數組類型
- : [];
- type 減一<某數 extends number> = 得到長度<數組減一<轉為數組<某數>>>;
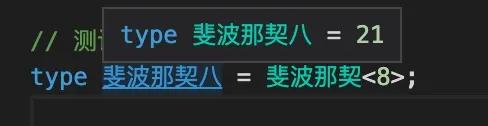
- // 測試
- type 斐波那契八 = 斐波那契<8>
看下結果:
不過到斐波那契 11 就因為遞歸層度太深 gg 了。
這里主要就是體驗下 TS 的圖靈完備,優化就不考慮了。
總結
通過寫一個這個例子對 TS 的類型有了更多的了解,但平時開發肯定不會這樣搞,主要是寫著玩哈哈,畢竟一個簡單的斐波那契數列都寫的這么麻煩,引用 Linus Torvalds 自傳的書名結束吧,Just for Fun!