模型泛化不必隨機(jī)訓(xùn)練全批量GD媲美SGD,網(wǎng)友:計(jì)算成本負(fù)擔(dān)不起
近來(lái)機(jī)器學(xué)習(xí)模型呈現(xiàn)出一種向大模型發(fā)展的趨勢(shì),模型參數(shù)越來(lái)越多,但依然具有很好的泛化性能。一些研究者認(rèn)為泛化性能得益于隨機(jī)梯度下降算法(SGD)所帶來(lái)的隨機(jī)噪聲。但最近一篇 ICLR 2022 的投稿《Stochastic Training is Not Necessary for Generalization》通過(guò)大量實(shí)驗(yàn)證實(shí)全批量的梯度下降算法(GD)可以達(dá)到與 SGD 不相上下的測(cè)試準(zhǔn)確率,且隨機(jī)噪聲所帶來(lái)的隱式正則化效應(yīng)可以由顯式的正則化替代。

論文地址:https://arxiv.org/pdf/2109.14119.pdf
該論文隨即在社區(qū)內(nèi)引發(fā)了一些討論,有人質(zhì)疑論文的含金量,覺(jué)得個(gè)例不具代表性:
也有人表示這篇論文就像一篇調(diào)查報(bào)告,提出的觀點(diǎn)和證明過(guò)程并無(wú)新意:

圖源:知乎用戶 @Summer Clover
雖然內(nèi)容有些爭(zhēng)議,但從標(biāo)題上看,這篇論文應(yīng)該包含大量論證,下面我們就來(lái)看下論文的具體內(nèi)容。
隨機(jī)訓(xùn)練對(duì)泛化并不是必需的
隨機(jī)梯度下降算法 (SGD) 是深度神經(jīng)網(wǎng)絡(luò)優(yōu)化的支柱,至少可以追溯 1998 年 LeCun 等人的研究。隨機(jī)梯度下降算法成功的一個(gè)核心原因是它對(duì)大型數(shù)據(jù)集的高效——損失函數(shù)梯度的嘈雜估計(jì)通常足以改進(jìn)神經(jīng)網(wǎng)絡(luò)的參數(shù),并且在整個(gè)訓(xùn)練集上可以比全梯度更快地進(jìn)行計(jì)算。
人們普遍認(rèn)為,隨機(jī)梯度下降 (SGD) 的隱式正則化是神經(jīng)網(wǎng)絡(luò)泛化性能的基礎(chǔ)。然而該研究證明非隨機(jī)全批量訓(xùn)練可以在 CIFAR-10 上實(shí)現(xiàn)與 SGD 相當(dāng)?shù)膹?qiáng)大性能。基于此,該研究使用調(diào)整后的超參數(shù),并表明 SGD 的隱式正則化可以完全被顯式正則化取代。研究者認(rèn)為這說(shuō)明:嚴(yán)重依賴隨機(jī)采樣來(lái)解釋泛化的理論是不完整的,因?yàn)樵跊](méi)有隨機(jī)采樣的情況下仍然可以得到很好的泛化性能。并進(jìn)一步說(shuō)明:深度學(xué)習(xí)可以在沒(méi)有隨機(jī)性的情況下取得成功。此外,研究者還表示,全批量訓(xùn)練存在感知難度主要是因?yàn)椋簝?yōu)化特性和機(jī)器學(xué)習(xí)社區(qū)為小批量訓(xùn)練調(diào)整優(yōu)化器和超參數(shù)所花費(fèi)的時(shí)間和精力不成比例。
具有隨機(jī)數(shù)據(jù)增強(qiáng)的全批量 GD
SGD 相對(duì)于 GD 有兩個(gè)主要優(yōu)勢(shì):首先,SGD 的優(yōu)化過(guò)程在穩(wěn)定性和超出臨界批量大小的收斂速度方面表現(xiàn)出質(zhì)的飛躍。其次,有研究表明,小批量上由步長(zhǎng)較大的 SGD 引起的隱式偏差可以用等式(5)和等式(7)中導(dǎo)出的顯式正則化代替。
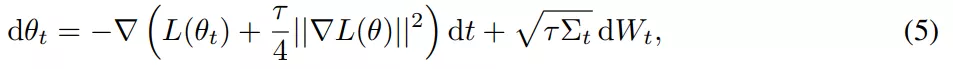
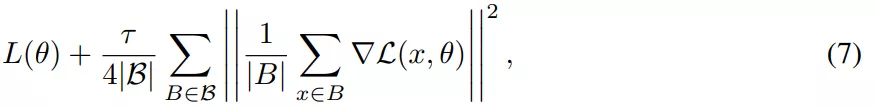
該研究對(duì)假設(shè)進(jìn)行了實(shí)證研究,試圖建立訓(xùn)練,使得在沒(méi)有來(lái)自小批量的梯度噪聲的情況下也能實(shí)現(xiàn)強(qiáng)泛化,核心目標(biāo)是實(shí)現(xiàn)全批量性能。因此該研究在 CIFAR-10 上訓(xùn)練了一個(gè)用于圖像分類(lèi)的 ResNet 模型進(jìn)行實(shí)驗(yàn)。
對(duì)于基線 SGD ,該研究使用隨機(jī)梯度下降進(jìn)行訓(xùn)練、批大小為 128 、 Nesterov 動(dòng)量為 0.9、權(quán)重衰減為 0.0005。
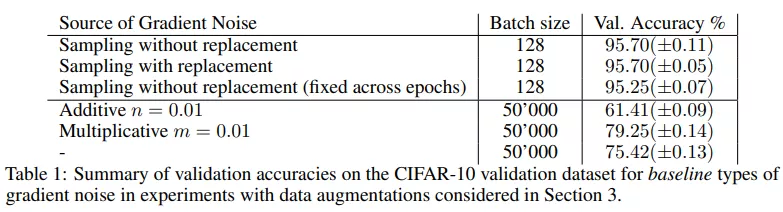
小批量 SGD 的驗(yàn)證準(zhǔn)確率達(dá)到了 95.70%(±0.05)。小批量 SGD 提供了一個(gè)強(qiáng)大的基線,在很大程度上是獨(dú)立于小批量處理的。如下表 1 所示,在有替換采樣時(shí)也達(dá)到相同的準(zhǔn)確率 95.70%。在這兩種情況下,隨機(jī)小批量處理引起的梯度噪聲都會(huì)導(dǎo)致很強(qiáng)的泛化。
然后,該研究將同樣的設(shè)置用于全批量梯度下降。用全批量替換小批量,并累積所有小批量梯度。為了排除批歸一化帶來(lái)的影響,該研究仍然在批大小為 128 的情況下計(jì)算批歸一化,在整個(gè)訓(xùn)練過(guò)程中將數(shù)據(jù)點(diǎn)分配給保持固定的一些塊,使得批歸一化不會(huì)引入隨機(jī)性。與其他大批量訓(xùn)練的研究一致,在這些設(shè)置下應(yīng)用全批量梯度下降的驗(yàn)證準(zhǔn)確率僅為 75.42%(±00.13),SGD 和 GD 之間的準(zhǔn)確率差距約為 20%。
該研究注意到,通過(guò)注入簡(jiǎn)單形式的梯度噪聲不容易彌補(bǔ)這一差距,如下表 1 所示。接下來(lái)的實(shí)驗(yàn)該研究努力縮小了全批量和小批量訓(xùn)練之間的差距。
由于全批量訓(xùn)練不穩(wěn)定,因此該研究在超過(guò) 400 step(每一個(gè) step 是一個(gè) epoch)的情況下將學(xué)習(xí)率從 0.0 提升到 0.4 以保持穩(wěn)定,然后在 3000 step 的情況下通過(guò)余弦退火衰減到 0.1。
實(shí)驗(yàn)表明在對(duì)訓(xùn)練設(shè)置進(jìn)行了一些修改后,全批量梯度下降性能提高到了 87.36%(±1.23),比基線提高了 12%,但仍與 SGD 的性能相去甚遠(yuǎn)。表 2 中總結(jié)了驗(yàn)證分?jǐn)?shù):
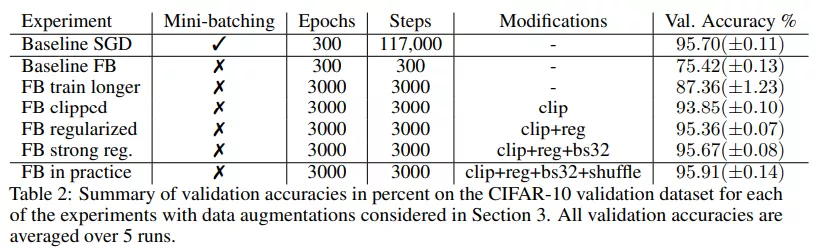
該研究用顯式正則化來(lái)彌補(bǔ)這種差距,并再次增加了初始學(xué)習(xí)率。在第 400 次迭代時(shí)將學(xué)習(xí)率增加到 0.8,然后在 3000 step 內(nèi)衰減到 0.2。在沒(méi)有正則化因子的情況下,使用該學(xué)習(xí)率和 clipping 操作進(jìn)行訓(xùn)練,準(zhǔn)確率為 93.75%(±0.13)。當(dāng)加入正則化因子時(shí),增大學(xué)習(xí)率的方法顯著提高了性能,最終與 SGD 性能相當(dāng)。
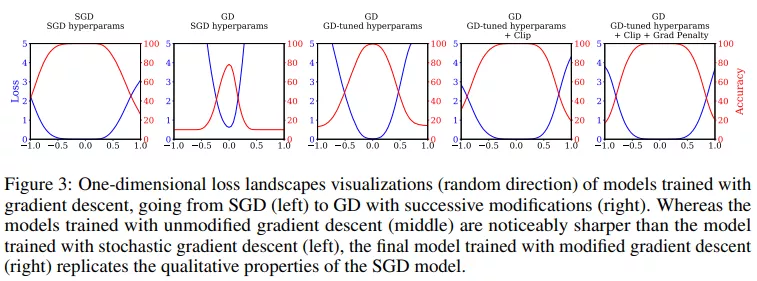
總體而言,該研究發(fā)現(xiàn)經(jīng)過(guò)所有修改后,全批量(帶有隨機(jī)數(shù)據(jù)增強(qiáng))和 SGD 的性能相當(dāng),驗(yàn)證準(zhǔn)確率顯著超過(guò) 95%。
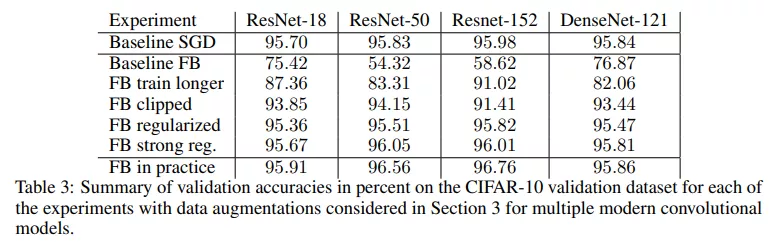
該研究還評(píng)估了一系列具有完全相同超參數(shù)的視覺(jué)模型。ResNet-50、ResNet-152 和 DenseNet-121 的結(jié)果見(jiàn)表 3,該研究發(fā)現(xiàn)所提方法也同樣適用于這些模型。
非隨機(jī)設(shè)置下的全批量梯度下降
如果全批量實(shí)驗(yàn)?zāi)軌虿蹲叫∨?SGD 的影響,那么隨機(jī)數(shù)據(jù)增強(qiáng)又會(huì)給梯度噪聲帶來(lái)什么影響?研究者又進(jìn)行了以下實(shí)驗(yàn)。
無(wú)數(shù)據(jù)增強(qiáng):如果不使用任何數(shù)據(jù)增強(qiáng)方法,并且重復(fù)之前的實(shí)驗(yàn),那么經(jīng)過(guò) clipping 和正則化的 GD 驗(yàn)證準(zhǔn)確率為 89.17%,顯著優(yōu)于默認(rèn)超參數(shù)的 SGD(84.32%(±1.12)),并且與新調(diào)整超參數(shù)的 SGD(90.07%(±0.48)) 性能相當(dāng),如下表 4 所示。

為了相同的設(shè)置下分析 GD 和 SGD,探究數(shù)據(jù)增強(qiáng)(不含隨機(jī)性)的影響,該研究使用固定增強(qiáng)的 CIFAR-10 數(shù)據(jù)集替換隨機(jī)數(shù)據(jù)增強(qiáng),即在訓(xùn)練前為每個(gè)數(shù)據(jù)點(diǎn)采樣 N 個(gè)隨機(jī)數(shù)據(jù)進(jìn)行數(shù)據(jù)增強(qiáng)。這些樣本在訓(xùn)練期間保持固定,也不會(huì)被重新采樣,從而產(chǎn)生放大 N 倍的 CIFAR-10 數(shù)據(jù)集。
最后,該研究得出結(jié)論:在沒(méi)有小批量、shuffling 以及數(shù)據(jù)增強(qiáng)產(chǎn)生的梯度噪聲后,模型也完全可以在沒(méi)有隨機(jī)性的情況下達(dá)到 95% 以上的驗(yàn)證準(zhǔn)確率。這表明,通過(guò)數(shù)據(jù)增強(qiáng)引入的噪聲可能不會(huì)影響泛化,并且也不是泛化所必需的。
引發(fā)討論
這篇論文在社區(qū)內(nèi)引發(fā)了大家的討論,有人從實(shí)驗(yàn)的角度分析了一下論文的價(jià)值。
該論文把 ResNet18 用 SGD 在 CIFAR-10 訓(xùn)練 300 個(gè) epoch 作為基線,并在結(jié)果部分展示了每一個(gè) trick 分別提升了多少準(zhǔn)確率。
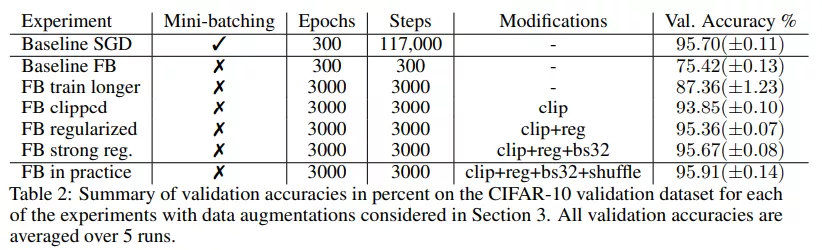
但是這幾個(gè) trick 太常見(jiàn)了,反而讓人質(zhì)疑真的如此有效嗎?有網(wǎng)友指出「train longer」這個(gè) trick 應(yīng)該只在 CIFAR-10 上這么有效,而 gradient clipping 在其他數(shù)據(jù)集上甚至可能無(wú)效。

圖源:知乎用戶 @Summer Clover
看來(lái)論文中的改進(jìn)可能是個(gè)例,難以代表一般情況。不過(guò),他也在評(píng)論中指出 SGD 近似正則化項(xiàng)
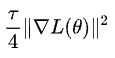
是個(gè)很有效的 trick,具備很好的理論基礎(chǔ),但是計(jì)算成本可能會(huì)翻倍:

圖源:知乎用戶 @Summer Clover
還有網(wǎng)友指出,這篇論文的研究結(jié)果實(shí)際用途很有限,因?yàn)槿吭O(shè)置的成本太高了,不是普通開(kāi)發(fā)者負(fù)擔(dān)得起的。相比之下,SGD 訓(xùn)練魯棒性強(qiáng),泛化性更好,也更省一次迭代的計(jì)算資源。
看來(lái)該論文進(jìn)行了一些理論和實(shí)驗(yàn)驗(yàn)證,但正如網(wǎng)友提議的:能否在其他數(shù)據(jù)集上進(jìn)行更多的實(shí)驗(yàn)來(lái)驗(yàn)證其結(jié)論?

對(duì)此,你怎么看?



























