性能分析不一定得用 Profiler,復雜度分析也行
如果提到性能分析,你會想到什么呢?
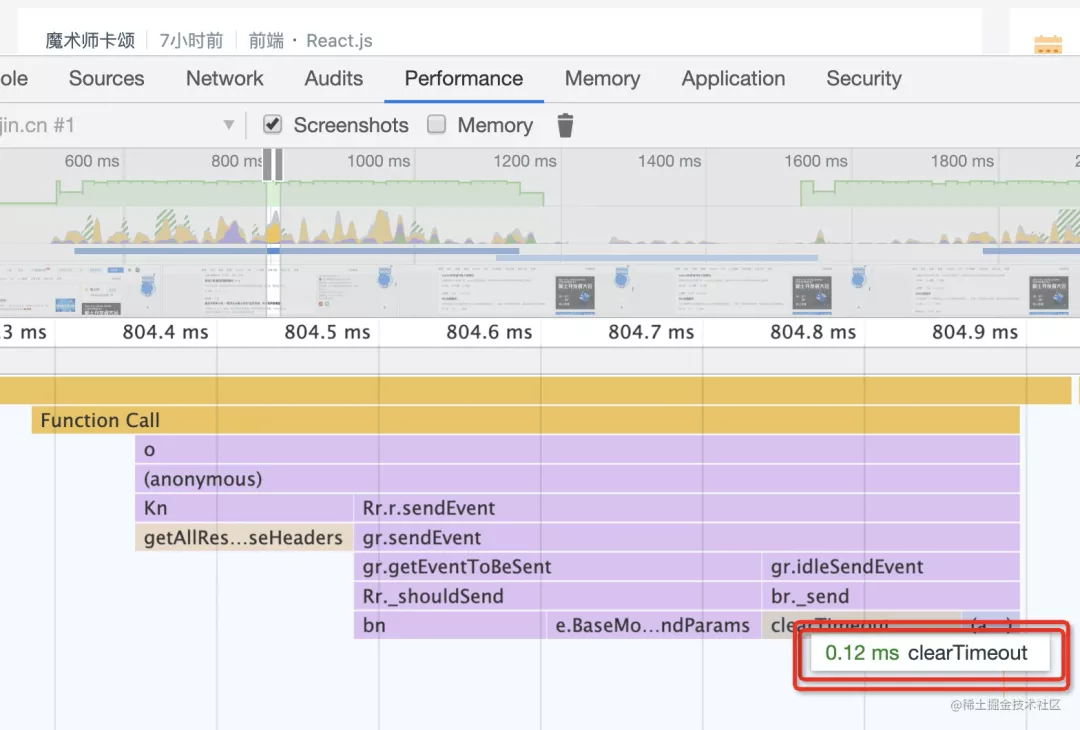
可以做耗時分析、內存占用的的分析。可以用 chrome devtools 的 Profiler,包括 performance 和 memory,分別拿到耗時和內存占用的數據,而且還可以用火焰圖做可視化分析。
比如 performance,你可以看到每個函數的耗時,通過簡單的加減法,就能算出是哪個函數耗時多,然后去優化。
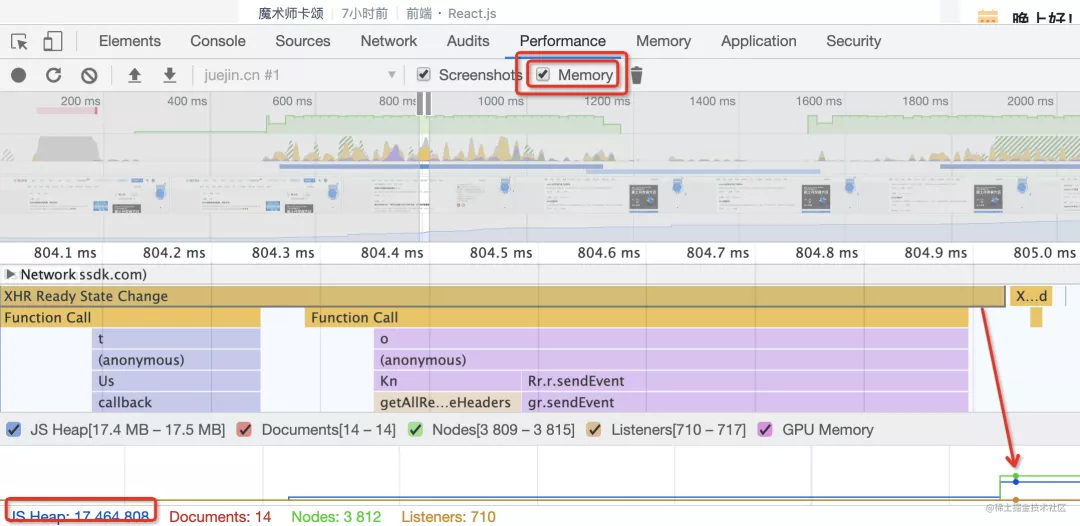
而且,你可以勾選 memory,顯示堆內存的變化,可以知道是哪個函數導致的內存增多,然后去優化。
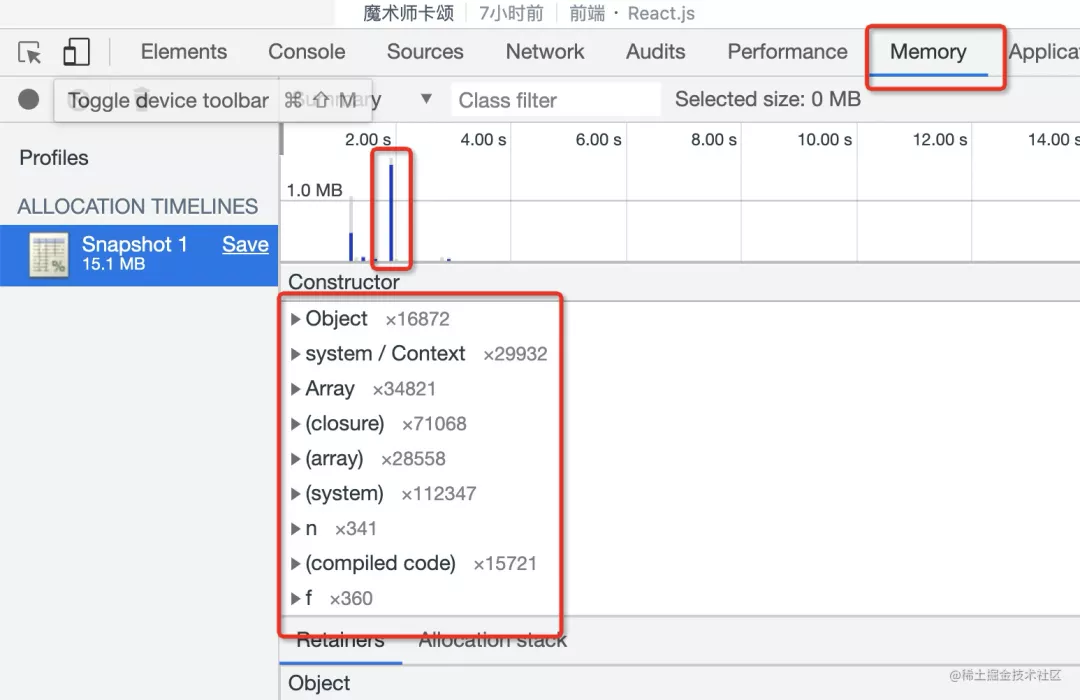
當然,你也可以單獨分析 memory 的 timeline,錄制一段時間的內存占用情況,然后看這時候的內存中有哪些對象,這樣比只知道大小更精確一些。
總之,我們可以通過調試工具的 Profiler 來看到內存和耗時,然后關聯到具體的函數,之后著手去優化。
但是,這些都是代碼跑起來才能統計的,而且與機器、不同的輸入數據等強相關。
如果換一臺機器,數據就是另一個樣子了。這也是為啥測試的時候要用各種機器測一遍。
那如果想代碼不運行就能估算出具體時間和內存占用大小,有什么思路么?
這就是復雜度分析技術做的事情了。
這篇文章我們來學下復雜度分析是如何估算時間的。
復雜度分析的幾個基礎
什么是 1,什么是 n
如果有這樣一行代碼:
- const name = 'guang';
耗時多少,內存多少?
你可能說得跑跑看,可能耗時 1ms,內存 4 bytes,也可能耗時 2ms,內存 8bytes 等等,不同的機器和運行環境都會有不同。
但我們都把它作為 1 ,這個 1 不是 ms,不是 byte,只是說是一個耗時/內存占用的基本單元,也就是復雜度是 1。
那這樣的代碼呢?
- function calc(n) {
- for(let i = 0; i < n; i ++) {
- //...
- }
- }
具體的數值隨著 n 的增大而增大,復雜度是 n。
我們分析復雜度的時候,不會分析具體的耗時和內存占用,而是以語句作為復雜度的單元,也就是 1,隨著輸入的數據規模 n 而變化的復雜度作為 n。
漸進的時候,常數可省略
我們知道了 1 和 n,就可以計算這些復雜度了:
- function func(n) {
- const a = 1;
- const b = 2;
- for (let i = 0; i < n; i ++) {
- //...
- }
- }
這里面有兩條語句,復雜度是 1 + 1,一個循環 n 次的語句,復雜度是 n,所以總復雜度是 2 + n。
- 復雜度(func) = 2 + n
當這個 n 逐漸變大的時候,比如 n 變成了 10000000,那這個 2 就可以忽略不計了。
也就是
- 復雜度(func) = O(n)
這個 O 是漸進復雜度的意思,也就是漸漸的增大的時候的復雜度。
有的同學說,這里是 2,所以可以省略,如果這里有 100000 條呢?是不是就不能省略了?
其實也會省略,因為不管多大,它的復雜度總是一個常數,是固定的,不會變化,所以不用分析進去,估算出的耗時或者內存占用加上它那固定的部分就可以了。而變化的部分才需要分析。
當我們計算漸進復雜度 O 的時候,常數會省略掉,因為它是固定的,不會變,而我們只分析變化的部分,也就是與 n 有關的部分。
多個變化的輸入數據規模時,都要計算
上面只是有一個輸入數據,規模是 n 的時候,復雜度與 n 有關。
如果有兩個輸入數據,規模分別為 m 和 n 的時候,那都要計算上,不能省略,因為都是變化的。
也就是 O(m + n)、 O(m * n) 這種。
一些常見的時間復雜度
我們明白了什么是 1,什么是 n,什么時候要同時計算 m 和 n,什么是漸進復雜度,為什么常數可以省略之后,就可以看一些實際的復雜度的例子了。
其實復雜度也就這么幾種:O(n)、O(n^2)、O(logn)、O(2^n)、O(n!)
O(n)
- function func(n) {
- const a = 1;
- for(let i = 0; i < n; i ++) {
- //...
- }
- }
這種就是 O(n),我們上面分析過。常數復雜度省略掉。
O(n^2) O(n^3)
- function func(n) {
- for(let i = 0; i < n; i ++) {
- for(let j = 0; j < n; j ++) {
- //...
- }
- }
- }
這種就是 O(n^2),同理,O(n^3)、O(n^4)等也一個意思,就是嵌套的時候,復雜度相乘。
O(logn)
- let n = 100;
- let i = 1;
- while(i < n){
- i = i * 2
- }
這段代碼要計算多少次,要看 i 乘以幾次 2 才大于 100,也就是 log2n
那同理,也有 log3n,log4n 等復雜度,當漸進復雜度的時候,常數是不用計算的,所以都是 O(logn)
o(2^n) o(3^n)
- const fibnacci = function (n) {
- if (n <= 1) return n;
- return fibnacci(n - 1) + fibnacci(n - 2);
- };
斐波那契數列我們都知道,可以用上面的遞歸來算。
這樣算的話,n 每加 1,就多遞歸調用了 2 次 fibnacci 函數,也就是復雜度乘以 2 了,所以復雜度是 O(2^n)。
同理,如果 n 每加一,多遞歸執行 3 次,那就是 O(3^n) 的復雜度。
也就是說,n 每加一,多遞歸 a 次,那復雜度就是 O(a^n)。
O(n!)
- function func(n) {
- for(let i=0; i<n; i++) {
- func(n-1);
- }
- }
上一條我們知道了,n 每加 1,多遞歸常數次,是指數型,那如果如果當 n 每加 1,多遞歸 n 次,這種就是復雜度 o(n!) 了。
為什么不是 O(n^n) 呢?因為 n 是變化的啊,所以是 O(n!)。
這基本是全部的時間復雜度情況了。當然,這里只是討論了 n 一個緯度,再多一個緯度 m 的話,也是一樣。
下面我們來區分一下這些時間復雜度的優劣。
時間復雜度的優劣對比
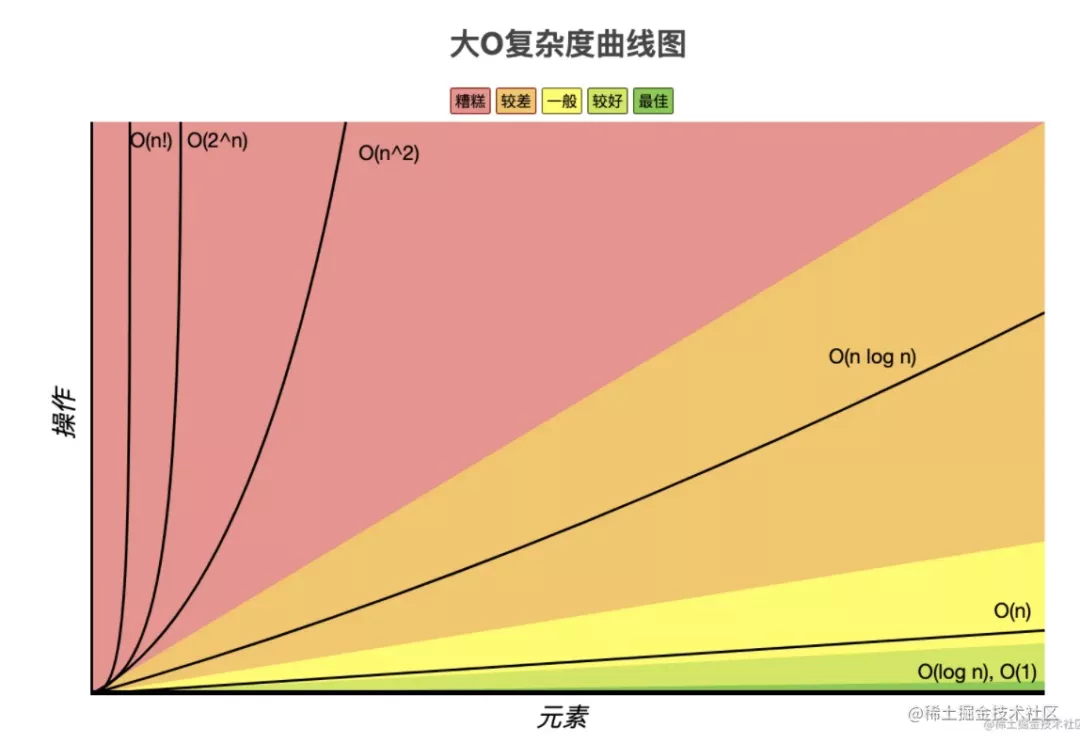
我們學習了大 O 的漸進時間復雜度表示法,就是為了估算 n 與具體執行時間的關系。上面分析出的幾種時間復雜度,它們與具體執行時間的關系是什么樣的呢?可以畫出變化函數來分析。
可以看到,隨著 n 的增大, O(n!) 和 O(2^n) 是耗時增加最快的,也就是說,這樣的代碼,n一旦大了,立馬會卡死,不用跑我們就能分析出來。
那什么樣是的不容易卡死的呢?O(n)、O(nlogn)、o(logn)這種,隨著數據規模的增大,耗時也不會增大很多。
所以我們說:
- O(n!)、O(2^n) 的時間復雜度都是特別高的,是不好的,是要避免的。
- O(n)、O(nlogn)、O(logn) 的時間復雜度是比較低的,是好的,是要盡量采用的。
根據這個結論,我們就可以評判一些代碼寫法的好壞,也就是算法的優劣了。
需要真實去跑代碼么?不需要。
空間復雜度
空間復雜度也就是堆棧內存的分配與輸入數據規模 n 的關系。
這里不包括全局變量,為什么呢?全局變量不會動態變啊,就相當于常數,可以省略,只分析變化的堆棧內存的復雜度就好了。
空間復雜度的分析方式和時間復雜度是類似的,只是不是把每一條語句作為 1,而是只把會分配內存的語句作為 1 來分析。
比如下面這段代碼的空間復雜度就是 O(n)。
- function func(n) {
- let arr = [];
- for (let i = 0; i < n; i++) {
- arr.push(i);
- }
- }
總結
分析性能一般通過運行時的 Profiler 來收集數據,然后分析耗時和內存占用,比如 chrome devtoos 的 performance 和 memory 工具。
但是其實不用運行代碼,我們也可以通過復雜度來估算出來:
我們把一條語句作為復雜度是 1,而隨著輸入數據規模 n 變化的為復雜度 n。
我們估算是為了分析出耗時/內存占用隨著數據規模 n 的一個變化關系,所以會用 O(n) 來表達這種變化關系,叫做漸進時間復雜度。
求漸進時間復雜度時,常數可以省略,因為它們是固定不變的,而我們只需要分析變化的部分。
復雜度基本就 O(n) O(logn) O(n^2) O(2^n) O(n!) 這幾種。
其中要注意的是 O(2^n) 就是當 n 每加一,多遞歸 2 次,而如果 n 每加 1,多遞歸 n 次,那么就是 O(n!) 的復雜度。
O(2^n) 和 O(n!) 的復雜度都是隨著 n 增加,復雜度急劇增加的,也就是耗時/內存占用會急劇增加,這樣的代碼很容易卡死,所以是不好的。
而 O(logn) O(n) 都是隨著 n 增加,復雜度增加很少的。也就意味了耗時更少,內存占用更少。這樣的算法當然也就更好了。
所以我們就是通過復雜度來評價算法好壞的,它就代表了耗時/內存占用,但不是直接表示的,而是抽象的表示。
如果說想得到不同機器、環境下的具體耗時/內存占用,那么就用 Profiler 在運行時收集數據,然后做分析和可視化,否則,其實通過復雜度就能夠抽象的估算出來大概的耗時和內存占用。
性能分析不一定得用 Profiler,復雜度分析也行,它能評價一個代碼寫法(算法)的好壞,進而估算出性能。