遞增子序列,有點難度!
給定一個整型數組, 你的任務是找到所有該數組的遞增子序列,遞增子序列的長度至少是2。
示例:
- 輸入: [4, 6, 7, 7]
- 輸出: [[4, 6], [4, 7], [4, 6, 7], [4, 6, 7, 7], [6, 7], [6, 7, 7], [7,7], [4,7,7]]
說明:
- 給定數組的長度不會超過15。
- 數組中的整數范圍是 [-100,100]。
- 給定數組中可能包含重復數字,相等的數字應該被視為遞增的一種情況。
思路
這個遞增子序列比較像是取有序的子集。而且本題也要求不能有相同的遞增子序列。
這又是子集,又是去重,是不是不由自主的想起了剛剛講過的90.子集II。
就是因為太像了,更要注意差別所在,要不就掉坑里了!
在90.子集II中我們是通過排序,再加一個標記數組來達到去重的目的。
而本題求自增子序列,是不能對原數組經行排序的,排完序的數組都是自增子序列了。
所以不能使用之前的去重邏輯!
本題給出的示例,還是一個有序數組 [4, 6, 7, 7],這更容易誤導大家按照排序的思路去做了。
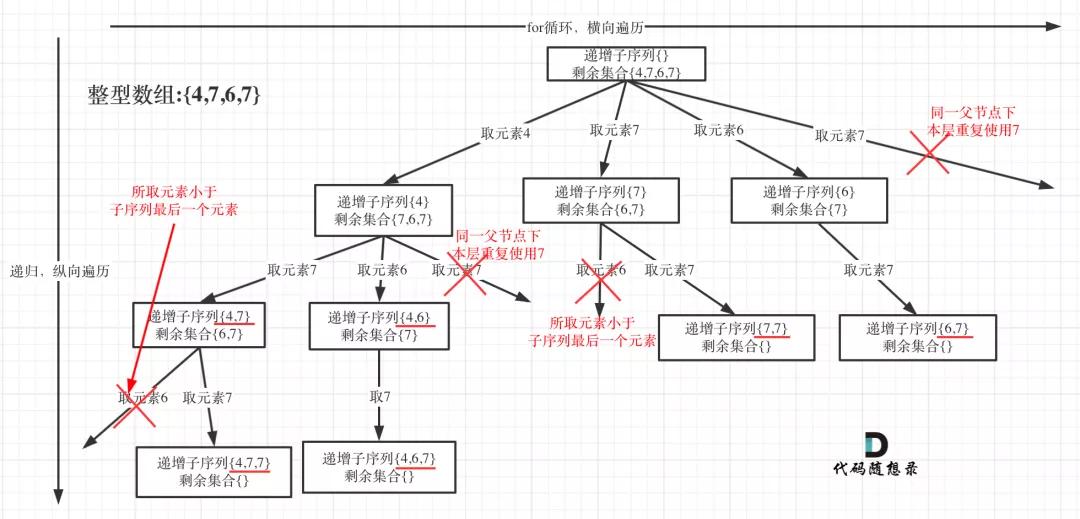
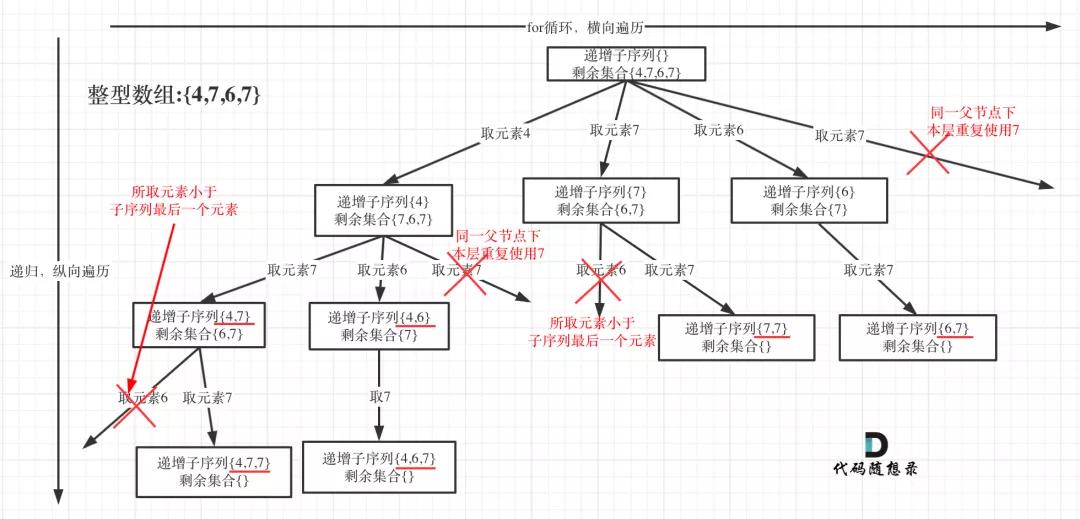
為了有鮮明的對比,我用[4, 7, 6, 7]這個數組來舉例,抽象為樹形結構如圖:
遞增子序列1
回溯三部曲
- 遞歸函數參數
本題求子序列,很明顯一個元素不能重復使用,所以需要startIndex,調整下一層遞歸的起始位置。
代碼如下:
- vector<vector<int>> result;
- vector<int> path;
- void backtracking(vector<int>& nums, int startIndex)
- 終止條件
本題其實類似求子集問題,也是要遍歷樹形結構找每一個節點,所以和回溯算法:求子集問題!一樣,可以不加終止條件,startIndex每次都會加1,并不會無限遞歸。
但本題收集結果有所不同,題目要求遞增子序列大小至少為2,所以代碼如下:
- if (path.size() > 1) {
- result.push_back(path);
- // 注意這里不要加return,因為要取樹上的所有節點
- }
- 單層搜索邏輯
在圖中可以看出,同一父節點下的同層上使用過的元素就不能在使用了
那么單層搜索代碼如下:
- unordered_set<int> uset; // 使用set來對本層元素進行去重
- for (int i = startIndex; i < nums.size(); i++) {
- if ((!path.empty() && nums[i] < path.back())
- || uset.find(nums[i]) != uset.end()) {
- continue;
- }
- uset.insert(nums[i]); // 記錄這個元素在本層用過了,本層后面不能再用了
- path.push_back(nums[i]);
- backtracking(nums, i + 1);
- path.pop_back();
- }
對于已經習慣寫回溯的同學,看到遞歸函數上面的uset.insert(nums[i]);,下面卻沒有對應的pop之類的操作,應該很不習慣吧,哈哈
這也是需要注意的點,unordered_set
最后整體C++代碼如下:
- // 版本一
- class Solution {
- private:
- vector<vector<int>> result;
- vector<int> path;
- void backtracking(vector<int>& nums, int startIndex) {
- if (path.size() > 1) {
- result.push_back(path);
- // 注意這里不要加return,要取樹上的節點
- }
- unordered_set<int> uset; // 使用set對本層元素進行去重
- for (int i = startIndex; i < nums.size(); i++) {
- if ((!path.empty() && nums[i] < path.back())
- || uset.find(nums[i]) != uset.end()) {
- continue;
- }
- uset.insert(nums[i]); // 記錄這個元素在本層用過了,本層后面不能再用了
- path.push_back(nums[i]);
- backtracking(nums, i + 1);
- path.pop_back();
- }
- }
- public:
- vector<vector<int>> findSubsequences(vector<int>& nums) {
- result.clear();
- path.clear();
- backtracking(nums, 0);
- return result;
- }
- };
優化
以上代碼用我用了unordered_set
其實用數組來做哈希,效率就高了很多。
注意題目中說了,數值范圍[-100,100],所以完全可以用數組來做哈希。
程序運行的時候對unordered_set 頻繁的insert,unordered_set需要做哈希映射(也就是把key通過hash function映射為唯一的哈希值)相對費時間,而且每次重新定義set,insert的時候其底層的符號表也要做相應的擴充,也是費事的。
那么優化后的代碼如下:
- // 版本二
- class Solution {
- private:
- vector<vector<int>> result;
- vector<int> path;
- void backtracking(vector<int>& nums, int startIndex) {
- if (path.size() > 1) {
- result.push_back(path);
- }
- int used[201] = {0}; // 這里使用數組來進行去重操作,題目說數值范圍[-100, 100]
- for (int i = startIndex; i < nums.size(); i++) {
- if ((!path.empty() && nums[i] < path.back())
- || used[nums[i] + 100] == 1) {
- continue;
- }
- used[nums[i] + 100] = 1; // 記錄這個元素在本層用過了,本層后面不能再用了
- path.push_back(nums[i]);
- backtracking(nums, i + 1);
- path.pop_back();
- }
- }
- public:
- vector<vector<int>> findSubsequences(vector<int>& nums) {
- result.clear();
- path.clear();
- backtracking(nums, 0);
- return result;
- }
- };
這份代碼在leetcode上提交,要比版本一耗時要好的多。
所以正如在哈希表:總結篇!(每逢總結必經典)中說的那樣,數組,set,map都可以做哈希表,而且數組干的活,map和set都能干,但如果數值范圍小的話能用數組盡量用數組。
總結
本題題解清一色都說是深度優先搜索,但我更傾向于說它用回溯法,而且本題我也是完全使用回溯法的邏輯來分析的。
相信大家在本題中處處都能看到是90.子集II的身影,但處處又都是陷阱。
對于養成思維定式或者套模板套嗨了的同學,這道題起到了很好的警醒作用。更重要的是拓展了大家的思路!
就醬,如果感覺「代碼隨想錄」很干貨,就幫Carl宣傳一波吧!
本文轉載自微信公眾號「代碼隨想錄」,可以通過以下二維碼關注。轉載本文請聯系代碼隨想錄公眾號。