[[424148]]

前幾天，有個(gè)朋友向我推薦了一個(gè)github 的開源項(xiàng)目https://github.com/OhBonsai/RedisTree, 可以用redis 直接讀寫polytree 的數(shù)據(jù)結(jié)構(gòu)，挺有意思的。那么， 什么是polytree 呢?

數(shù)據(jù)結(jié)構(gòu)與樹

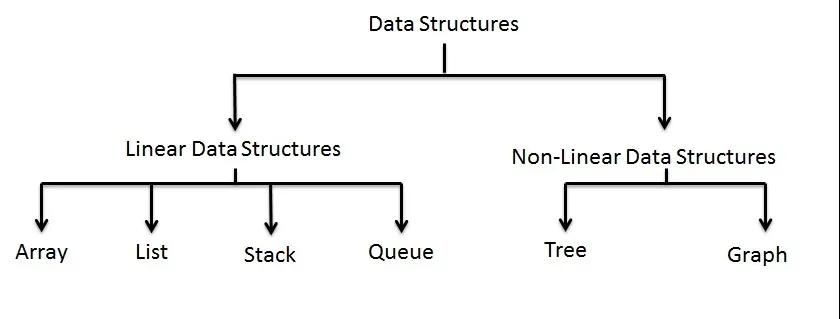
當(dāng)我們說數(shù)據(jù)結(jié)構(gòu)的時(shí)候，在我們的腦海里呈現(xiàn)的可能是一棵如下的樹：

也就是說， 數(shù)據(jù)結(jié)構(gòu)大體可以分為兩類：線性數(shù)據(jù)結(jié)構(gòu)和非線性數(shù)據(jù)結(jié)構(gòu)。線性數(shù)據(jù)結(jié)構(gòu)中常見的有數(shù)組，鏈表，棧和隊(duì)列;非線性數(shù)據(jù)結(jié)構(gòu)主要是樹和圖。

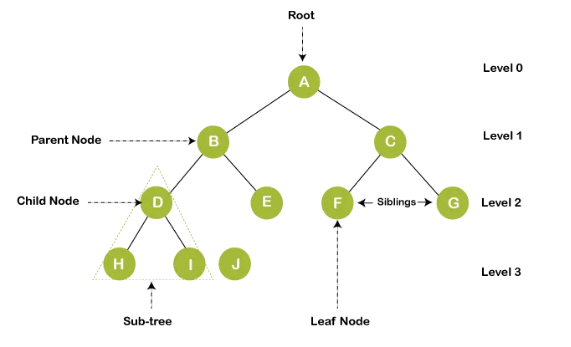
雖然不是自舉，但我們實(shí)際上用『樹』來描述了數(shù)據(jù)結(jié)構(gòu)。樹數(shù)據(jù)結(jié)構(gòu)定義為對(duì)象或?qū)嶓w(稱為節(jié)點(diǎn))的集合，這些對(duì)象或?qū)嶓w鏈接在一起以表示或模擬層次結(jié)構(gòu)。樹數(shù)據(jù)結(jié)構(gòu)是一種非線性數(shù)據(jù)結(jié)構(gòu)，因?yàn)樗话错樞虼鎯?chǔ)。它是一種層次結(jié)構(gòu)，因?yàn)闃渲械脑乇话才旁诙鄠€(gè)級(jí)別。『樹』中的常用術(shù)語大致如下：

基于樹中子節(jié)點(diǎn)的多少以及子節(jié)點(diǎn)自身的屬性，形成了各種各樣的樹，且樹的應(yīng)用場(chǎng)景非常廣泛，例如計(jì)算機(jī)系統(tǒng)的文件系統(tǒng)，計(jì)算簡(jiǎn)單或復(fù)雜的數(shù)學(xué)表達(dá)式，這時(shí)的樹是一種特殊的樹，稱為表達(dá)式樹，二叉樹支持O(logN)平均時(shí)間內(nèi)的搜索操作等等。

polytree 及其特點(diǎn)

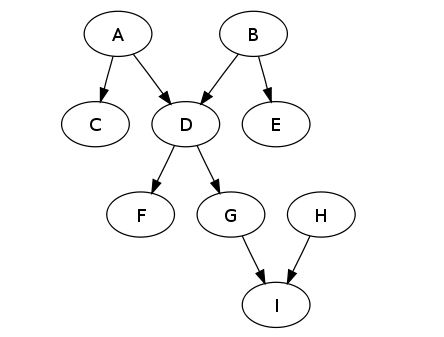
polytree一詞由Rebane和Pearl于1987年創(chuàng)造。Polytree是一個(gè)有向無環(huán)圖的特例，任意兩個(gè)頂點(diǎn)之間最多有一條無向路徑的圖。換句話說，一個(gè)有向無環(huán)圖，其中可從任何節(jié)點(diǎn)到達(dá)的子圖形成一棵樹。關(guān)于有向無環(huán)圖可以參考《有向無環(huán)圖(DAG)的溫故知新》。

圖是一個(gè)神奇的東西，圖論是應(yīng)用數(shù)學(xué)中應(yīng)用極其廣泛的一類，在計(jì)算機(jī)科學(xué)中也是如此，日常生活中其實(shí)也很廣泛;任意一種網(wǎng)絡(luò)，都是一種圖;思維導(dǎo)圖也是一種圖;鄙視鏈同樣是一種圖;網(wǎng)格其實(shí)也是圖，等等。不管是什么結(jié)構(gòu)，只要結(jié)構(gòu)中的對(duì)象存在一種二元聯(lián)系，就總可以找到一個(gè)圖來描述它，用一些有向邊或無向邊把一些點(diǎn)連起來，無所謂其中邊的長度;如果是多元關(guān)系，可以用超圖表示。

具體考慮一個(gè) polytree，線性預(yù)處理可以插入中間節(jié)點(diǎn)并折疊只有一個(gè)子節(jié)點(diǎn)的節(jié)點(diǎn)，從而得到一個(gè)polytree，可以使用該polytree來回答對(duì)原始polytree的查詢，因此，可以在不損失一般性的情況下假設(shè)?? 正好有2個(gè)度。按照任何拓?fù)漤樞蜃缘紫蛏线M(jìn)行線性時(shí)間預(yù)處理，對(duì)于每個(gè)節(jié)點(diǎn)?? 我們將為節(jié)點(diǎn)構(gòu)造一個(gè)索引結(jié)構(gòu)，我們稱之為“中綴樹(infix tree)”，它還可能包括指向其他先前定義的此類結(jié)構(gòu)的指針。

在線性時(shí)間內(nèi)構(gòu)造polytree，對(duì)于任何節(jié)點(diǎn)，都可以通過恒定延遲枚舉其中綴樹。

中綴樹中有三種節(jié)點(diǎn)：

• 葉子節(jié)點(diǎn)，用至少一個(gè)且最多四個(gè)元素的顯式集合標(biāo)記(是原始polytree的葉子);
• 小型內(nèi)部節(jié)點(diǎn)，用一個(gè)顯式元素和指向一個(gè)或兩個(gè)中綴樹節(jié)點(diǎn)的指針標(biāo)記;
• 大型內(nèi)部節(jié)點(diǎn)，用兩個(gè)顯式元素和指向一個(gè)或兩個(gè)中綴樹節(jié)點(diǎn)的指針標(biāo)記。

進(jìn)一步要求中綴樹中沒有重復(fù)的元素，即，對(duì)于中綴樹的每個(gè)節(jié)點(diǎn)??，P 的每一片葉子在標(biāo)簽中最多顯示一次??。節(jié)點(diǎn)?? 在中綴樹中，是對(duì)P的葉子節(jié)點(diǎn)進(jìn)行編碼的集合??(??)。中綴樹的思想是，通過保留一些顯式元素，我們既可以在枚舉時(shí)使用它們，以便快捷地訪問節(jié)點(diǎn)，也可以在合并時(shí)使用它們，以便有足夠多的元素來標(biāo)準(zhǔn)中綴樹中新創(chuàng)建的節(jié)點(diǎn)。

索引的數(shù)據(jù)結(jié)構(gòu)將polytree的每個(gè)節(jié)點(diǎn)?? 映射到可到達(dá)的葉子節(jié)點(diǎn) ??(??) ，??(??(??)) 是??中的節(jié)點(diǎn)可達(dá)的葉子節(jié)點(diǎn)集合。那么，可以得到Polytree 的兩個(gè)如下特性：

• 在線性時(shí)間內(nèi)可以做到這一點(diǎn);
• 可以在恒定的延遲中完成枚舉。

polytree的應(yīng)用

polytree樹的典型應(yīng)用之一是用作概率推理的圖模型。如果貝葉斯網(wǎng)絡(luò)具有polytree的結(jié)構(gòu)，則可以使用信念傳播有效地對(duì)其進(jìn)行推理。

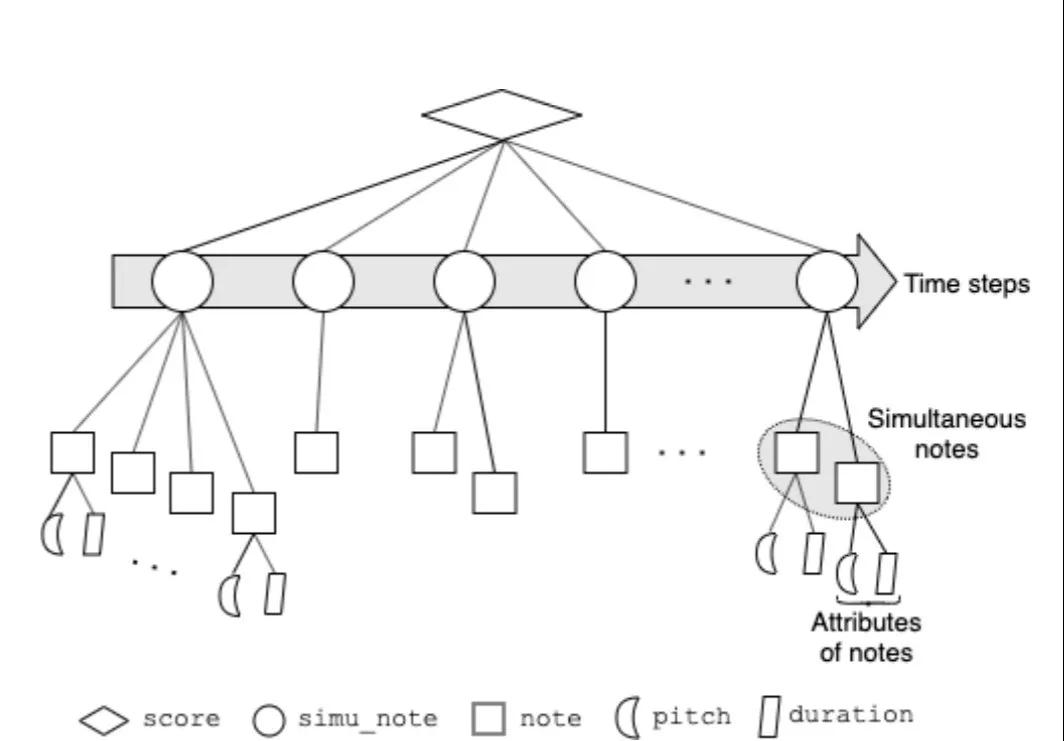
實(shí)際上，polytree還有很多更為具體的應(yīng)用，例如復(fù)調(diào)音樂是一種共時(shí)、離散的時(shí)間序列，通常被表示為一維的events序列，或者二維的piano roll，缺點(diǎn)是music knowledge不夠多，不能體現(xiàn)復(fù)調(diào)音樂的內(nèi)在結(jié)構(gòu)。而基于polytree的樹結(jié)構(gòu)，包含三個(gè)級(jí)別：時(shí)間序列——音符——音符屬性。

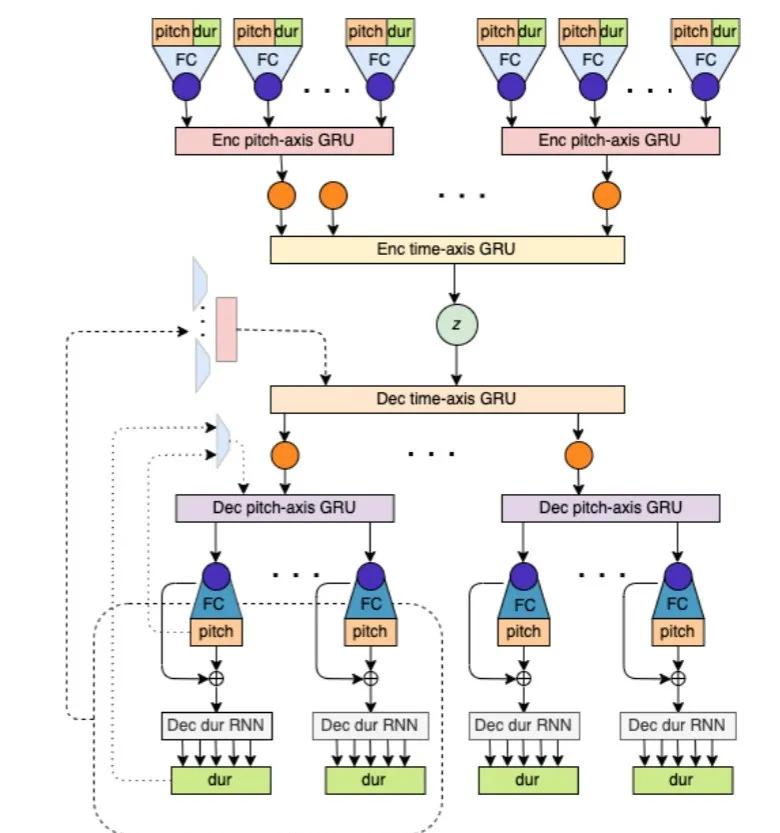
再以一個(gè)Encoder-Decoder網(wǎng)絡(luò)來學(xué)習(xí)復(fù)調(diào)音樂的latent representation，整體模型架構(gòu)如下：

在鋼琴表征學(xué)習(xí)任務(wù)實(shí)驗(yàn)結(jié)果顯示，polytree在重建準(zhǔn)確性和模型泛化方面優(yōu)于baseline。

幾乎同名的prollytree

創(chuàng)造新名詞是IT界的最愛， 國內(nèi)外差不多都是如此。Norms 為了創(chuàng)建一個(gè)類似git 的去中心化數(shù)據(jù)庫，提出了Prolly Tree，雖然幾乎同音，但實(shí)際上咫尺天涯。

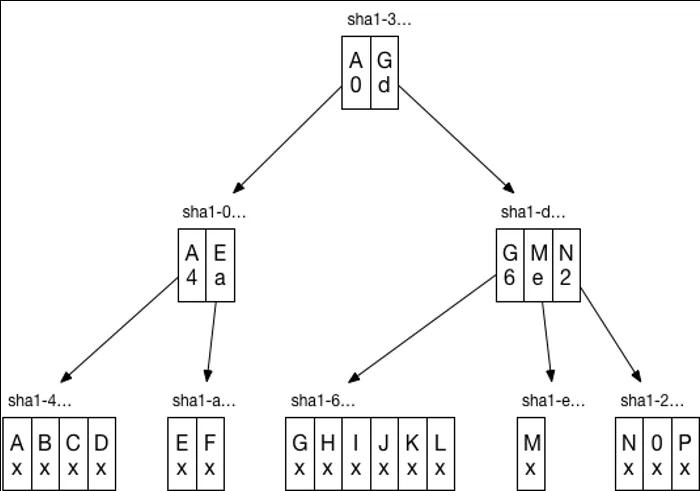
Prolly Tree 全稱是Probabilistic Merkle B-Trees，集成了B樹和merkle 樹，結(jié)構(gòu)示例如下：

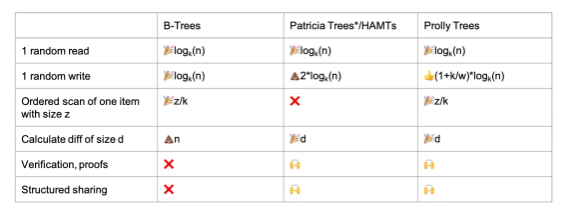
因此，prolly tree 具有B樹高效隨機(jī)讀寫和有序掃描的特性，同時(shí)擁有merkle 樹的可驗(yàn)證性以及包括/排除的可證明性，具體的屬性如下表所示：

Norms 項(xiàng)目以prollytree 作為核心的數(shù)據(jù)結(jié)構(gòu)，試圖實(shí)現(xiàn)一個(gè)去中心化的數(shù)據(jù)庫，是一個(gè)積極的嘗試。

小結(jié)

當(dāng)覺得它沒有什么意思的時(shí)候，或許是因?yàn)槲覀儗?duì)它缺乏了解;當(dāng)覺得它有點(diǎn)意思的時(shí)候，或許我們才剛剛走在了應(yīng)用的路上。老碼農(nóng)對(duì)polytree的感知如是，給予不同的約束，我們可以得到不同的樹，進(jìn)而應(yīng)用到不同的業(yè)務(wù)場(chǎng)景。

參考資料

• Incremental Dynamic Construction of Layered Polytree Networks，https://arxiv.org/abs/1302.6833
• https://ldzhangyx.github.io/2019/10/30/polytree/
• https://www.microsoft.com/en-us/research/wp-content/uploads/2016/05/prml-slides-8.pdf
• https://cstheory.stackexchange.com/questions/37262/efficient-enumeration-of-the-reachable-leaves-of-nodes-in-a-polytree
• https://github.com/attic-labs/noms