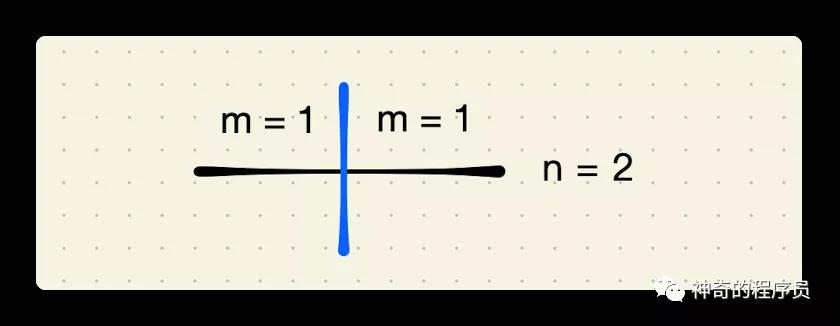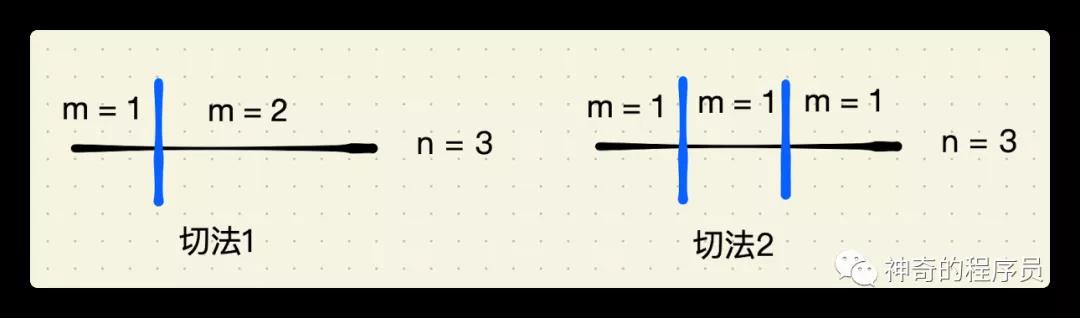一篇學(xué)會理解動態(tài)規(guī)劃
本文轉(zhuǎn)載自微信公眾號「神奇的程序員」,作者神奇的程序員。轉(zhuǎn)載本文請聯(lián)系神奇的程序員公眾號。
前言
動態(tài)規(guī)劃是一種比較難以理解的算法思想,本文結(jié)合自己的理解采用通俗易懂的方式來講解下動態(tài)規(guī)劃,歡迎各位感興趣的開發(fā)者閱讀本文。
思路分析
接下來,我們通過一個例子來逐步分析,引出動態(tài)規(guī)劃思想。
假設(shè),你家里三種面值的鈔票(1元、5元、11元)無數(shù)張,現(xiàn)在需要用這些鈔票湊出某個金額出來,我們需要怎樣搭配才能用最少的鈔票數(shù)量湊出這個金額出來?
例如:我們要湊15元出來。
貪心思想 - 只顧眼前
依據(jù)我們的生活經(jīng)驗,肯定是先用面紙較大的鈔票,用總金額做減法運算,思路如下:
- 先拿1張11元的鈔票,接下來我們要湊的金額就是4元(15 - 11)
- 要湊4元出來,我們只能用1元鈔票來湊,我們需要4張1元紙幣(4 - 1 - 1 - 1 - 1)
15元湊出來了,我們總共用了5張鈔票(1張11元的,4張1元的)。這種策略,我們稱之為貪心,我們把要湊的金額設(shè)為w,需要用的鈔票面額設(shè)為m,貪心策略會盡快的讓w變的更小,每減少一次,我們接下來要面對的局面就是湊出w - m。
經(jīng)過我們大腦計算后,這種策略湊出15元所用的鈔票數(shù)量并不是最少的,我們直接使用3張5元的鈔票就可以湊這個金額。
更好的方案 - 動態(tài)規(guī)劃
我們使用貪心思想來解決這個問題時,只考慮了眼前的情況,格局小了,那么我們現(xiàn)在應(yīng)該如何避免這種情況呢?
如果使用暴力枚舉的方法來湊出金額,明顯時間復(fù)雜度過高,太多種組合方式可以湊出這個金額了,枚舉它們的時間是不可承受的。
重疊子問題
接下來,我們來嘗試著,找一下這個問題的性質(zhì)。
- 一開始,如果我們?nèi)×嗣嬷禐?1的鈔票,那么接下來面臨的問題就是湊出金額為4時所需的最少鈔票數(shù)量
- 一開始,如果我們?nèi)×嗣嬷禐?的鈔票,那么接下來面臨的問題就是湊出金額為10時所需的最少鈔票數(shù)量
- 一開始,如果我們?nèi)×嗣嬷禐?的鈔票,那么接下來面臨的問題就是湊出金額為14時所需的最少鈔票數(shù)量
經(jīng)過上述分析,我們會發(fā)現(xiàn)這些問題都有一個共同的形式:給定一個金額,湊出這個金額所需的最少鈔票數(shù)量。
我們將一個大問題拆解成了三個子問題。
接下來,我們再來分析下這三個子問題,我們用f(n)來表示湊出n所需的最少鈔票數(shù)量,用cost來表示湊出w所需的鈔票數(shù)量,那么:
如果我們?nèi)×?1,最后用掉的鈔票總數(shù)就為:cost = f(4) + 1
如果我們?nèi)×?,最后用掉的鈔票總數(shù)就為:cost = f(10) + 1
如果我們?nèi)×?,最后用掉的鈔票總數(shù)就為:cost = f(14) + 1
觀察上述問題后,我們會發(fā)現(xiàn)一個共同點:每取一個面值的鈔票,都需要計算剩余金額所需的最少鈔票數(shù),而它們的計算方法都是相同的。
這三個子問題都需要用同一種方式求解,那么它們就屬于重疊子問題。
最優(yōu)子結(jié)構(gòu)
當(dāng)我們要湊出15元的金額時,我們需要的鈔票總數(shù)就為上述三種情況里所需鈔票數(shù)量最少的那一個。
我們在求f(n)時,又要算出金額為n時所需的最少鈔票數(shù),例如f(10),我們只能用2種面值的鈔票(5元的和1元的)
如果用5元來湊的話,我們需要的鈔票數(shù)就為:f(5) + 1
如果用1元來湊的話,我們需要的鈔票數(shù)就為:f(9) + 1
我們在求f(n)時,一定會從其子問題的解決方案中找出所需硬幣數(shù)量最少的那個,即:
f(n) = min(f(n - 1), f(n -5 ), f(n - 11)) + 1
大問題的最優(yōu)解可以由子問題的最優(yōu)解推出,這個性質(zhì)就稱為最優(yōu)子結(jié)構(gòu)。
無后效性
通過上面的分析,我們知道了金額為15時,需要求出3個重疊子問題的解,選出最優(yōu)的那個就是最終問題的解。
那三個子問題又有自己的重疊子問題,我們在求解這些重疊子問題時,只需要知道最終答案,不用去關(guān)心他們是如何算出來的,因為他們的計算過程并不會對之后的問題產(chǎn)生影響。
例如:f(4), f(10), f(14) ,我們只需要求出他們的具體值,他們的計算過程對我們之后要求解的問題沒有影響。
如果給定某一階段的狀態(tài),這一階段以后過程的發(fā)展,不受這階段以前各段狀態(tài)的影響,就稱為無后效性,即:未來與過去無關(guān)。
剪繩子
有一根長度為n的繩子,把繩子剪成m段(m、n都是整數(shù),n > 1并且m > 1),每段繩子的長度記為k[0], k[1], ..., k[m]。
請問k[m] * k[1] * ... * k[m]可能的最大乘積是多少?
例如:當(dāng)繩子長度為8時,我們把它剪成長度分別為2、3、3的三段,此時得到的最大乘積是18。
思路分析
接下來,我們來分析這個例子,看看能否用動態(tài)規(guī)劃來解決。
根據(jù)題意,我們可知下述信息:
- 繩子的長度肯定大于1且每次至少切一刀
- 我們用f(n)來表示長度為n的繩子所有切法的最大乘積
那么,當(dāng)繩子的長度為2時,我們只有一種切法,從中間切,這條繩子會被切為長度各為1的兩小段,如下圖所示:
當(dāng)n=2時,f(n) = 1 * 1 = 1,即:f(2) = 1
我們繼續(xù)分析n=3的情況,如下圖所示,它有2種切法
- 切成長度為1和長度為2的兩小段
- 切成長度分別為1、1、1的三小段
從切法2中,我們可以看出它其實就是對長度為2的繩子進(jìn)行了一次切分,經(jīng)過前面的分析,我們已經(jīng)知道了它的所有切法的最大乘積是1,那么他們的乘積就是1 * 1 * 1 = 1。
因此, 我們不對他進(jìn)行劃分,直接取切法1的乘積,即: f(3) = 2
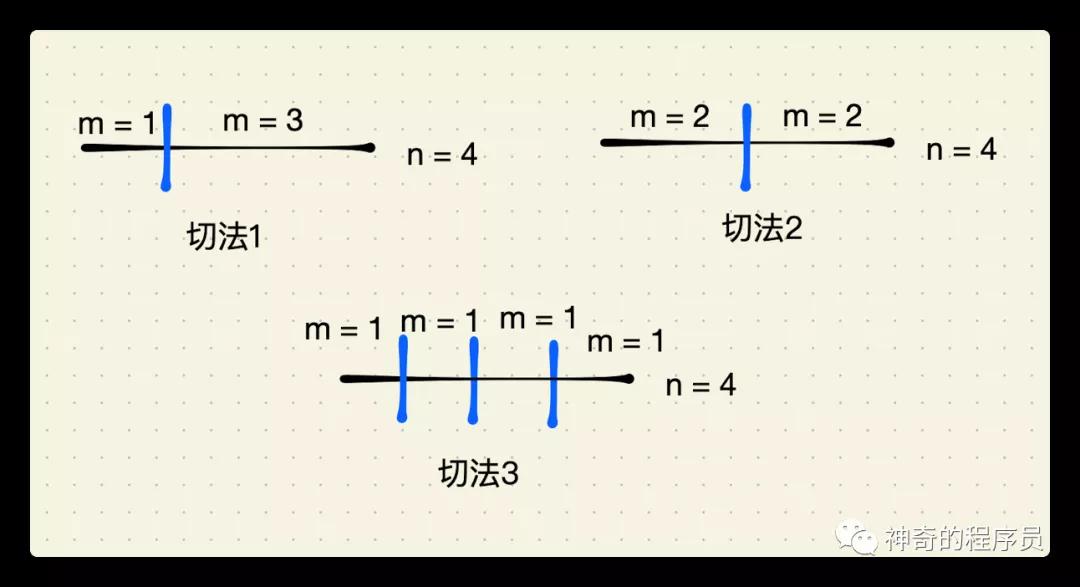
我們再來看下n=4的情況,如下圖所示,它有3種切法
- 切成長度為1和長度為3的兩小段
- 切成長度為2和長度為2的兩小段
- 切長度為別為1的四小段
從切法1中,我們可以看出長度為3的那一段繩子的最大乘積我們已經(jīng)算出來了(f(3) = 2),如果我們對這段繩子進(jìn)行切分的話,乘積就變小了,所以我們選擇不切分這部分繩子,那么切法1的最大乘積就為1 * 3 = 3。
從切法2中,我們可以看出那兩段繩子的長度都為2,而長度為2的繩子的最大乘積我們也已經(jīng)算出來了(f(2) = 1),如果切分的話,乘積就變小了,那么切法2的最大乘積就為2 * 2 = 4。
綜上所述,我們可以發(fā)現(xiàn)這樣一條規(guī)律:
- 無論繩子最終被切成多少段,它肯定是一刀一刀來切分的
- 繩子長度為2或者3時,不會再進(jìn)行切分了,直接取其長度
那么,對于一條繩子來說,它一旦被切了一刀,就會被劃分為2個子問題:
- 切割點左側(cè)的繩子怎么切
- 切割點右側(cè)的繩子怎么切
因為我們是從1開始往后推的,前面的繩子怎么切,我們已經(jīng)存起來了。
分析到這里,我們發(fā)現(xiàn)它已經(jīng)滿足動態(tài)規(guī)劃的2個特性了:
- 重疊子問題:繩子被切開后,每一部分的繩子還可能再繼續(xù)進(jìn)行切分,每次切分要面臨的子問題都是一樣的
- 最優(yōu)子結(jié)構(gòu):對每部分的繩子進(jìn)行切分時,我們都需要求出這部分繩子的所有切法中最大乘積是多少,滿足了最優(yōu)子結(jié)構(gòu)這個特性
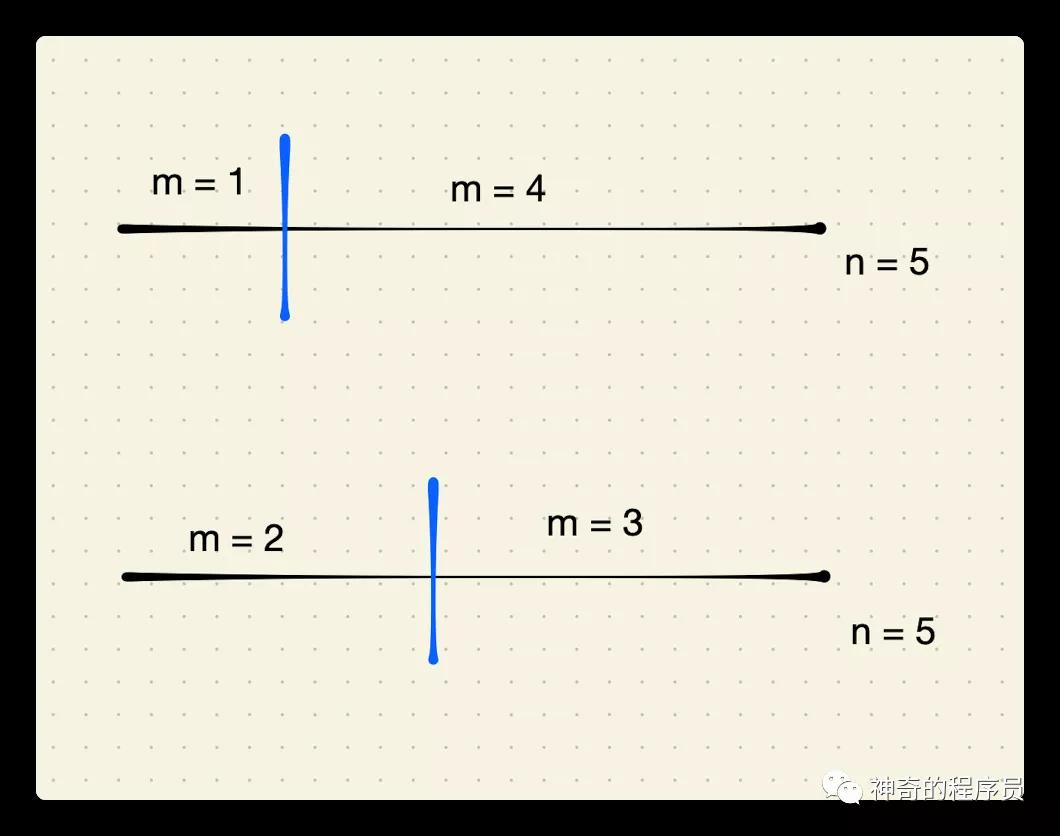
我們再來分析下n=5的情況,如下圖所示,我們的第一刀有兩種切法:從1位置、從2位置切,分別可以將繩子切為:
- 長度為1和長度為4的兩小段
- 長度為2和長度為3的兩小段
我們用一個數(shù)組(result)將前面已經(jīng)求出來的繩子的最大乘積(最優(yōu)解)存起來,綜上所述,我們知道了當(dāng)繩子長度小于4時,每段繩子長度的最大乘積是固定的,即:
- result[0] = 0
- result[1] = 1
- result[2] = 2
- result[3] = 3
注意:因為繩子至少要切一刀且繩子的長度大于1,所以當(dāng)繩子長度為1時是沒法進(jìn)行裁切的,因此它的最大乘積為1。
當(dāng)繩子長度為2或3時,我們不會對它進(jìn)行切分,因此他們的最大乘積就是其本身的長度。
觀察上圖后我們發(fā)現(xiàn),當(dāng)繩子長度大于等于4時,第一刀要的位置切法最多只能切到繩子長度一半的位置,每次切分出來的子問題,我們在前面已經(jīng)算過并且放進(jìn)了result中,我們只需將每種切法的子問題最優(yōu)解相乘取出最大值即可。
當(dāng)n=4時,第一刀可以切的位置可以是:1、2:
- result[4] = max(result[1] * result[3], result[2] * result[2])
- = max(1 * 3, 2 * 2)
- = max(3, 4)
- = 4
當(dāng)n=5時,第一刀可以切的位置可以是:1、2:
- result[5] = max(result[1] * result[4], result[2] * result[3])
- = max(1 * 4, 2 * 3 )
- = max(4, 6)
- = 6
當(dāng)n = 6時,第一刀可以切的位置可以是:1、2、3
- result[6] = max(result[1] * result[5], result[2] * result[4], result[3] * result[3])
- = max(1 * 6, 2 * 4, 3 * 3)
- = max(6, 8, 9)
- = 9
研究到這里,我們會發(fā)現(xiàn)在求子問題的最優(yōu)解時,我們只關(guān)心它的結(jié)果,它的計算過程并不會影響到我們最終問題的解,那么它也滿足了動態(tài)規(guī)劃的最后一個性質(zhì):無后效性
遞推公式
經(jīng)過上面的一系列的推導(dǎo),我們發(fā)現(xiàn)這個問題已經(jīng)滿足了動態(tài)規(guī)劃的三個性質(zhì),那么也就是說這個問題是可以用動態(tài)規(guī)劃來解決的。
經(jīng)過上面的分析,我們知道了不管怎么切,繩子都會被切成兩部分,然后再分別求解這兩部分的最大乘積,那么當(dāng)繩子長度為n時,我們就能得到如下所示的公式:
- result[n] = result[i] * result[n - i]
n為當(dāng)前要求的繩子長度,i為當(dāng)前要切割位置。
繩子的不管從哪個位置切,都會被切成兩段,我們求出這兩段的乘積,求出每種切法的最大乘積就是長度為n的繩子的最大乘積。
實現(xiàn)代碼
經(jīng)過上面的一系列分析,我們已經(jīng)徹底掌握了這道題的解法,思路有了,我們就可以用代碼將其實現(xiàn)了,如下所示(TypeScript代碼):
- public cutTheRope(length: number): number {
- // 由于繩子只能整數(shù)切,所以繩子長度小于2時,無法進(jìn)行裁剪
- if (length < 2) {
- return 0;
- }
- // 繩子長度為2時,只能從中間裁剪, 所有切法的最大乘積為1
- if (length === 2) {
- return 1;
- }
- // 繩子長度為3時,可以切成:
- // 1. 1 1 1
- // 2. 1 2
- // 1 * 2 > 1 * 1 * 1, 故長度為3時, 所有切法的最大乘積為2
- if (length === 3) {
- return 2;
- }
- // 創(chuàng)建結(jié)果數(shù)組,存儲每段長度繩子切分時的最大乘積
- const products = new Array<number>(length + 1);
- // 長度小于4時,繩子的最大乘積我們已經(jīng)推算出來了,因此直接保存即可
- products[0] = 0;
- products[1] = 1;
- // 繩子長度為2或3時,不進(jìn)行拆分,最大乘積為繩子的長度
- products[2] = 2;
- products[3] = 3;
- // 繩子長度大于4時需要對繩子進(jìn)行切分,求出切分后的每段繩子的最大乘積
- for (let i = 4; i <= length; i++) {
- // 賦初始值
- products[i] = 0;
- // 當(dāng)前長度繩子的最大乘積
- let max = 0;
- // 至少切一刀,從繩子的1位置開始切,切到i/2位置。
- // 求出長度為i時,切一刀后兩段繩子的最大乘積
- for (let j = 1; j <= i / 2; j++) {
- // 根據(jù)遞推公式求當(dāng)前裁剪位置的兩段繩子的乘積
- const product = products[j] * products[i - j];
- // 比對歷史切法中兩段繩子的最大乘積和當(dāng)前切法兩段繩子的乘積
- if (max < product) {
- // 替換最大值
- max = product;
- }
- // 修改當(dāng)前繩子長度切法的最大乘積
- products[i] = max;
- }
- }
- // 每種長度繩子的最大乘積都已經(jīng)求出,length位置的值就是整個問題的解
- return products[length];
- }
完整代碼請移步:DynamicProgramming.ts[1]
編寫測試用例
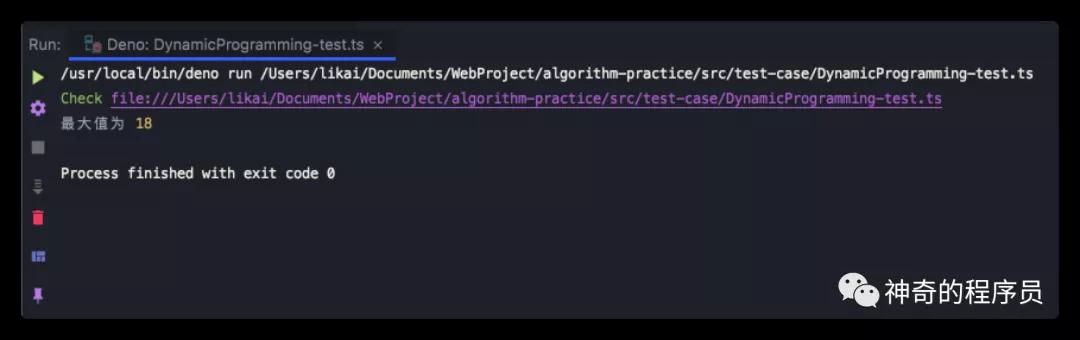
我們將題目中求長度為8的繩子帶入帶入上述代碼中,求出最大值來驗證下我們的代碼是否是正確的,如下所示:
- import DynamicProgramming from "../DynamicProgramming.ts";
- const dynamicProgrammingTest = new DynamicProgramming();
- const maxVal = dynamicProgrammingTest.cutTheRope(8);
- console.log("最大值為", maxVal);
完整代碼請移步:DynamicProgramming-test.ts[2]
運行結(jié)果如下:
同類型例子
當(dāng)你讀完本文后,相信你對動態(tài)規(guī)劃已經(jīng)有了一定的理解,緊接著你可以嘗試的做一下其他能用動態(tài)規(guī)劃解決的問題,加深下理解,達(dá)到徹底掌握的目的。
我還寫了其他幾個動態(tài)規(guī)劃問題的分析文章,如果你對此感興趣,請移步:
- 最少硬幣找零問題[3]
- 背包問題[4]
- 最長公共子序列[5]
- 矩陣鏈相乘[6]
寫在最后
至此,文章就分享完畢了。
我是神奇的程序員,一位前端開發(fā)工程師。
公眾號無法外鏈,如果文中有鏈接,可點擊下方閱讀原文查看??
參考資料
[1]DynamicProgramming.ts: https://github.com/likaia/algorithm-practice/blob/a31acfe5c9b3acbf51c9383a09003611b64ea16b/src/DynamicProgramming.ts#L9
[2]DynamicProgramming-test.ts: https://github.com/likaia/algorithm-practice/blob/7fda8ff39d15ab7a4030bd998a63e1ec331117c9/src/test-case/DynamicProgramming-test.ts
[3]最少硬幣找零問題: https://juejin.cn/post/6869571836066299912#heading-7
[4]背包問題: https://juejin.cn/post/6869571836066299912#heading-10
[5]最長公共子序列: https://juejin.cn/post/6869571836066299912#heading-13
[6]矩陣鏈相乘: https://juejin.cn/post/6869571836066299912#heading-16