[[417618]]

本文轉(zhuǎn)載自微信公眾號「bigsai」，作者bigsai。轉(zhuǎn)載本文請聯(lián)系程序員bigsai公眾號。

前言

大家好,我是bigsai,今天給大家講講Dijkstra算法，下次拿著這個(gè)算法找女神少繞路，有女朋友的可以試試行不行的通。

對于Dijkstra算法,很多人可能感覺熟悉而又陌生,可能大部分人比較了解bfs和dfs,而對dijkstra和floyd算法可能知道大概是圖論中的某個(gè)算法,但是可能不清楚其中的作用和原理,又或許,你曾經(jīng)感覺它很難,那么,這個(gè)時(shí)候正適合你重新認(rèn)識它。

Dijkstra是啥?

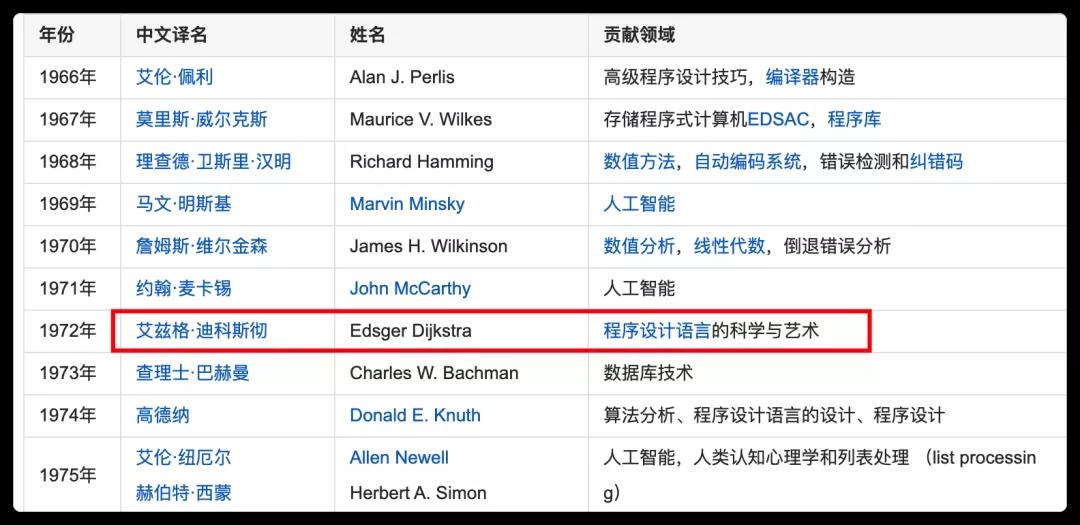
其實(shí)Dijkstra(迪科斯徹)是一個(gè)人,被稱為結(jié)構(gòu)程序設(shè)計(jì)之父,他提出goto有害論、信號量、原語等,創(chuàng)造解決銀行家算法、哲學(xué)家進(jìn)餐問題、Dijkstra算法等等,在1972年獲得圖靈獎(計(jì)算機(jī)界諾?爾獎),今天咱們就學(xué)習(xí)Dijkstra算法。

Dijkstra算法干啥的?

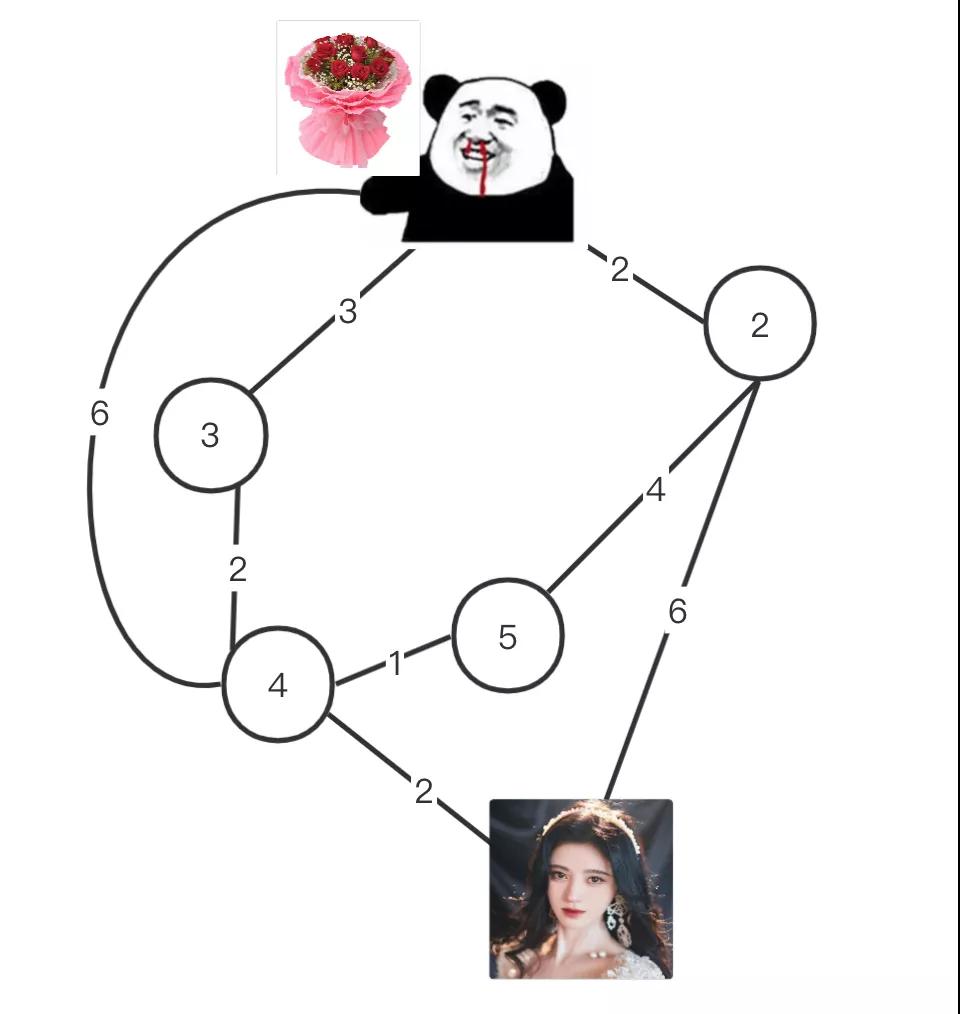
Dijkstra是用來求單源最短路徑的,也就是在一個(gè)圖中,從一個(gè)點(diǎn)計(jì)算到達(dá)其他點(diǎn)的最短距離,再形象一點(diǎn),就是比如七夕你捧著鮮花去找女神,有點(diǎn)距離,在不堵?沒紅綠燈情況下怎么找到一條最短的路徑:

這不是一眼就能看出來嘛!還要什么算法?enum,如果路徑很多像這樣呢?

就拿上圖來說,如果各條路?度都已知,那么可以使用dijkstra算法計(jì)算你到圖中所有節(jié)點(diǎn)的最短距離(不過你想要的就是和女神的距離最近)。不過這個(gè)單源最短路徑你可能產(chǎn)生一些疑惑:

單源什么意思?

一個(gè)源頭,從一個(gè)頂點(diǎn)出發(fā),Dijkstra算法只能求一個(gè)頂點(diǎn)到其他點(diǎn)的最短距離而不能任意兩點(diǎn)。

和bfs求的最短路徑有什么區(qū)別?

bfs求的與其說是路徑,不如說是次數(shù)。因?yàn)閎fs他是按照隊(duì)列一次一次進(jìn)行加入相鄰的點(diǎn),而兩點(diǎn)之間沒有權(quán)值或者權(quán)值相等(代價(jià)相同)。bfs求最短路徑一般無權(quán)值路徑(只代表聯(lián)通性)或者權(quán)值相等,僅僅用次數(shù)就能表示路徑?短的情況,最典型的就是迷宮問題bfs搜索移動一次路徑為1就加一次。

Dijkstra在處理具體實(shí)例的應(yīng)用還是很多的,因?yàn)榫唧w的問題其實(shí)帶權(quán)更多一些。比如一個(gè)城市有多個(gè)鄉(xiāng)鎮(zhèn),鄉(xiāng)鎮(zhèn)可能有道路,也可能沒有,整個(gè)鄉(xiāng)鎮(zhèn)需要聯(lián)通,如果想計(jì)算每個(gè)鄉(xiāng)鎮(zhèn)到a鎮(zhèn)的最短路徑,那么Dijkstra就派上了用場。

算法分析

對于一個(gè)算法,首先要理解它的運(yùn)行流程,對于Dijkstra算法而言,首先要知道其適用條件和環(huán)境:

一個(gè)連通圖,若干節(jié)點(diǎn)(節(jié)點(diǎn)可能有數(shù)值),但是路徑一定有權(quán)值并且不能為負(fù)(否則Dijkstra就不適用)。

Dijkstra的核心思想是貪心算法的思想,那什么是貪心呢?

貪心算法(又稱貪婪算法)是指,在對問題求解時(shí),總是做出在當(dāng)前看來是最好的選擇。也就是說,不從整體最優(yōu)上加以考慮,他所

做出的是在某種意義上的局部最優(yōu)解。

貪心算法不是對所有問題都能得到整體最優(yōu)解,關(guān)鍵是貪心策略的選擇,選擇的貪心策略必須具備無后效性,即某個(gè)狀態(tài)以前的過程不會影響以后的狀態(tài),只與當(dāng)前狀態(tài)有關(guān)。

對于貪心算法,在很多情況都能用到,下面舉2個(gè)不恰當(dāng)?shù)睦?

1 .上學(xué)時(shí),每周只能帶5個(gè)蘋果,你想帶最多,那么選五個(gè)蘋果你每次都選最大的那個(gè)五次下來你就選的最重的那個(gè)。

2 .錢幣找零,指定幣值和相應(yīng)的數(shù)量,用最少的數(shù)量湊?某金額。利用貪心策略,優(yōu)先選擇面值大的錢幣,直到湊?總金額。

3 .活動選擇問題,知道多個(gè)活動開始時(shí)間、結(jié)束時(shí)間,想在一個(gè)時(shí)間內(nèi)參加最多活動,按照活動結(jié)束時(shí)間遞增排序即可。

上面的策略雖然沒有很強(qiáng)的理論數(shù)學(xué)依據(jù),或者不太好說明,更像一種事實(shí)規(guī)律經(jīng)驗(yàn),并且對于貪心問題具體處理上大部分都需要排序,還可能會遇到規(guī)則繁雜的類排序。那么我們的Dijkstra是如何貪心的呢?對于一個(gè)點(diǎn),求圖中所有點(diǎn)的最短路徑,如果沒有正確的方法胡亂想確實(shí)很難算出來,并且如果暴力匹配復(fù)雜度呈指數(shù)級上升不適合解決實(shí)際問題。那么我們該怎么想呢?

首先,Dijkstra算法實(shí)現(xiàn)上需要這些前提:

• Dijkstra處理的是帶正權(quán)值的有權(quán)圖,那么就需要一個(gè)二維數(shù)組(如果空間大用List數(shù)組)存儲各個(gè)點(diǎn)到點(diǎn)之間邊的權(quán)值大小 (鄰接矩陣或者鄰接表存儲) ，各個(gè)點(diǎn)距離初始化為無窮大。
• 需要一個(gè)boolean數(shù)組判斷哪些點(diǎn)已經(jīng)確定最短?度路徑,那些點(diǎn)沒有確定。用一個(gè) int數(shù)組記錄距離(在算法執(zhí)行過程有些點(diǎn)最短路徑可能被多次更新)。
• 需要優(yōu)先隊(duì)列加入已經(jīng)確定點(diǎn)的周圍點(diǎn)。每次拋出從起點(diǎn)最短路徑的那個(gè)點(diǎn),直到所有點(diǎn)路徑確定最短為止。

簡單的概括流程為:

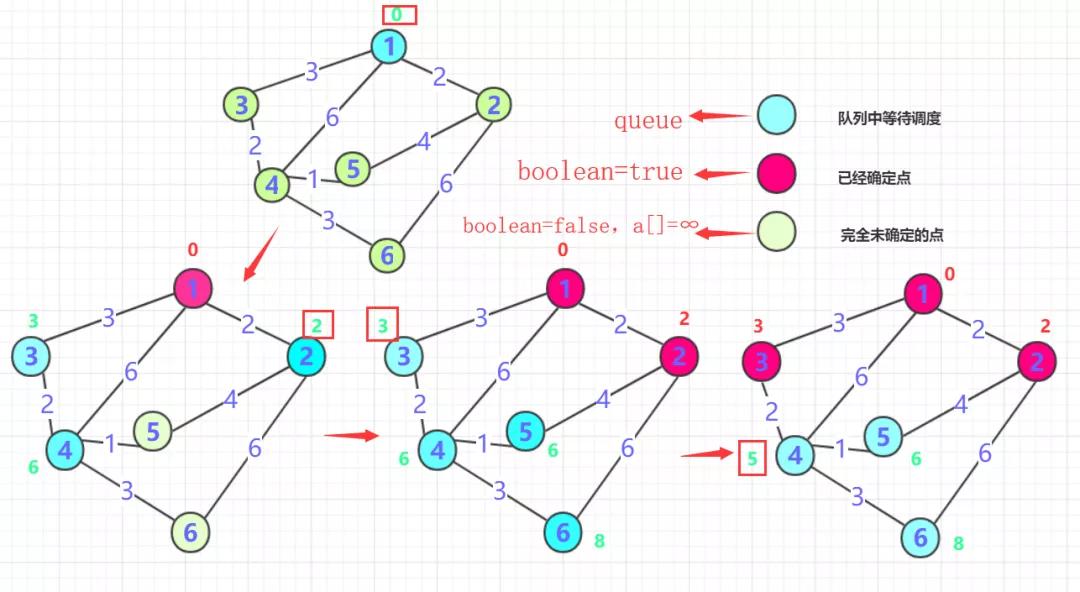
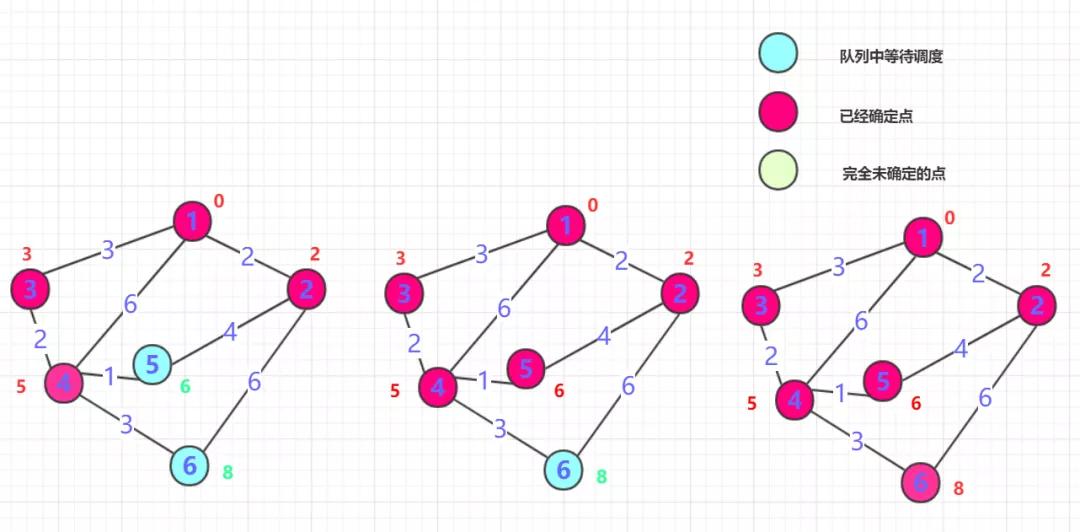
第一步一般從選定點(diǎn)開始拋入優(yōu)先隊(duì)列(路徑一般為0),boolean數(shù)組標(biāo)記0的位置(最短為0) , 然后0周圍連通的點(diǎn)拋入優(yōu)先隊(duì)列中(可能是node類),并把各個(gè)點(diǎn)的距離記錄到對應(yīng)數(shù)組內(nèi)，此時(shí)周圍點(diǎn)只是等待調(diào)度可能是最短距離，也可能被更新。(如果小于就更新,大于就不動,初始第一次是無窮肯定會更新),第一次就結(jié)束了。

從等待調(diào)度隊(duì)列中拋出距離最近的那個(gè)點(diǎn)B(第一次就是0周圍鄰居)。這個(gè)點(diǎn)距離一定是最近可以確定的(所有權(quán)值都是正的,點(diǎn)的距離只能越來越?，而它的路徑是所有可能中的最小的)標(biāo)記這個(gè)點(diǎn)為true表示已經(jīng)確定,并且將這個(gè)點(diǎn)的鄰居加入隊(duì)列(下一次等待調(diào)度點(diǎn)為隊(duì)列中原有的和這個(gè)點(diǎn)周圍未確定的鄰居),并同時(shí)判斷是否更新B點(diǎn)鄰居?度,如果小于則更新!

重復(fù)二的操作,直到所有點(diǎn)都確定。

算法實(shí)現(xiàn)

代碼實(shí)現(xiàn)上面有些繁瑣，但是也不是很復(fù)雜，這里給個(gè)Dijkstra算法實(shí)現(xiàn)代碼：

package 圖論; 
 
import java.util.ArrayDeque; 
import java.util.Comparator; 
import java.util.PriorityQueue; 
import java.util.Queue; 
import java.util.Scanner; 
 
public class dijkstra { 
    static class node 
    { 
        int x; //節(jié)點(diǎn)編號 
        int lenth;//長度 
        public node(int x,int lenth) { 
            this.x=x; 
            this.lenth=lenth; 
        } 
    } 
 
    public static void main(String[] args) { 
 
        int[][] map = new int[6][6];//記錄權(quán)值，順便記錄鏈接情況，可以考慮附加鄰接表 
        initmap(map);//初始化 
        boolean bool[]=new boolean[6];//判斷是否已經(jīng)確定 
        int len[]=new int[6];//長度 
        for(int i=0;i<6;i++) 
        { 
            len[i]=Integer.MAX_VALUE; 
        } 
        Queue<node>q1=new PriorityQueue<node>(com); 
        len[0]=0;//從0這個(gè)點(diǎn)開始 
        q1.add(new node(0, 0)); 
        int count=0;//計(jì)算執(zhí)行了幾次dijkstra 
        while (!q1.isEmpty()) { 
            node t1=q1.poll(); 
            int index=t1.x;//節(jié)點(diǎn)編號 
            int length=t1.lenth;//節(jié)點(diǎn)當(dāng)前點(diǎn)距離 
            bool[index]=true;//拋出的點(diǎn)確定 
            count++;//其實(shí)執(zhí)行了6次就可以確定就不需要繼續(xù)執(zhí)行了  這句可有可無，有了減少計(jì)算次數(shù) 
            for(int i=0;i<map[index].length;i++) 
            { 
                if(map[index][i]>0&&!bool[i]) 
                { 
                    node node=new node(i, length+map[index][i]); 
                    if(len[i]>node.lenth)//需要更新節(jié)點(diǎn)的時(shí)候更新節(jié)點(diǎn)并加入隊(duì)列 
                    { 
                        len[i]=node.lenth; 
                        q1.add(node); 
                    } 
                } 
            } 
        }        
        for(int i=0;i<6;i++) 
        { 
            System.out.println(len[i]); 
        } 
    } 
    static Comparator<node>com=new Comparator<node>() { 
 
        public int compare(node o1, node o2) { 
            return o1.lenth-o2.lenth; 
        } 
    }; 
 
    private static void initmap(int[][] map) { 
        map[0][1]=2;map[0][2]=3;map[0][3]=6; 
        map[1][0]=2;map[1][4]=4;map[1][5]=6; 
        map[2][0]=3;map[2][3]=2; 
        map[3][0]=6;map[3][2]=2;map[3][4]=1;map[3][5]=3; 
        map[4][1]=4;map[4][3]=1; 
        map[5][1]=6;map[5][3]=3;     
    } 
} 

當(dāng)然,dijkstra算法比較靈活,實(shí)現(xiàn)方式也可能有點(diǎn)區(qū)別,但是思想是不變的:一個(gè)貪心思路。dijkstra執(zhí)行一次就能夠確定一個(gè)點(diǎn),所以只需要執(zhí)行點(diǎn)的總和次數(shù)即可完成整個(gè)算法。

一句話概況一下，就是從一個(gè)點(diǎn)開始找周圍最短的一個(gè)，更新相應(yīng)數(shù)據(jù)，再找已經(jīng)確定直接連接的第二個(gè)最短點(diǎn)、第三個(gè)一直到所有點(diǎn)確定，dijkstra算法就完成了。