正所謂“平時不努力，考試靠兄弟，”考試臨近，作弊狂魔張三又在琢磨如何在期末考試中作弊了。

已知張三所在的學校，針對考試有兩個特別的規定：

• 試卷在考試前密封，監考老師不知道考題，也不能在考試時，查看學生的試卷內容，所以老師無法知道正確答案。
• 抓學生作弊講證據，即便發現學生在傳紙條，如果老師無法理解或解密紙條上的內容，就不能定性為學生作弊。

當然，這個學校的老師，有豐富的反作弊經驗，像什么摸左耳代表B，摸右耳代表A之類的，根本逃不過老師的法眼。

[[398937]]

對稱加密

一直夢想著成為一名黑客的他，前天好像翻過一本關于網絡信息安全的書籍，里面提到一種加密方法叫“對稱加密”。

這是一種使用同一個密鑰進行加密和解密的方法。

數據發送方將明文和加密密鑰通過特殊的算法處理后，使其變成很復雜的加密密文，然后發送給數據接收方，數據接收方再使用加密密鑰和相同算法的逆算法，對密文進行解密，將密文恢復成明文。

張三想：

讓學習成績好的哥們兒李四，把正確答案寫在紙條上，用對稱加密的方法對答案進行加密，再傳給我，就算老師拿到了紙條，看不懂上面的內容，就拿我沒辦法了!

說干就干，張三設計了以下作弊步驟流程：

• 張三私底下告訴李四：“y=3(密鑰)。”
• 在考場黑板上寫上：x+y=z(x表示答案，z表示加密后，寫在紙條上的密文)
• 李四根據這一算法，加密答案，把z的值寫在答案上，傳給張三
• 張三拿到紙條，用y的值進行解密，還原答案

這樣一來，由于y=3(密鑰)只有張三和李四知道，監考老師即使拿到了紙條，由于沒有y的值，無法解密紙條上的內容，也就拿他沒辦法了。

張三把想法告訴了李四，李四沉思了一會兒，告訴他其中存在的風險：

(1) 怎么保證密鑰不泄露?

萬一我們在商量密鑰的時候，被其他同學知道了，向老師告密，那我們的心血就白白浪費了。

(2) 密鑰管理起來很難

假如李四這道題不會，只能求救王五，你還得和王五商量一個密鑰，假如王五不會，你還得和其他同學商量一個密鑰，如此一來，密鑰非常多，萬一記錯了怎么辦?

的確，對稱加密有很多缺點。

非對稱加密

不甘心的張三回去又開始翻書了，這回他找到了一個更好的方法——非對稱加密。

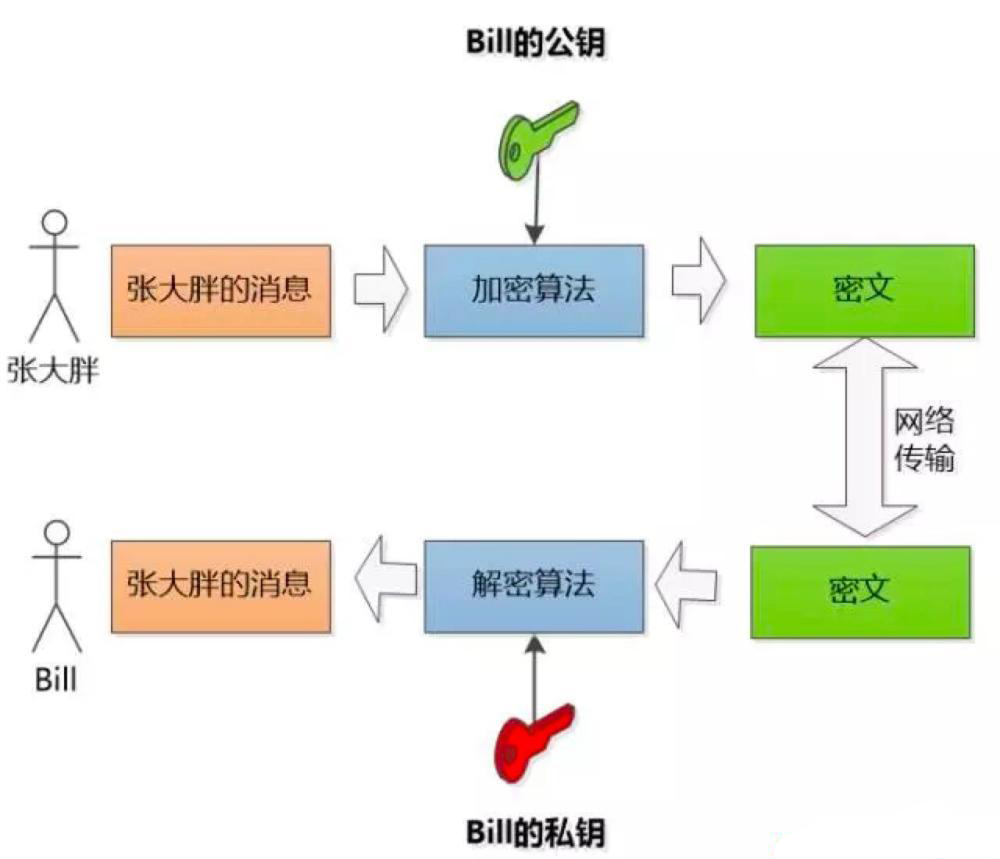
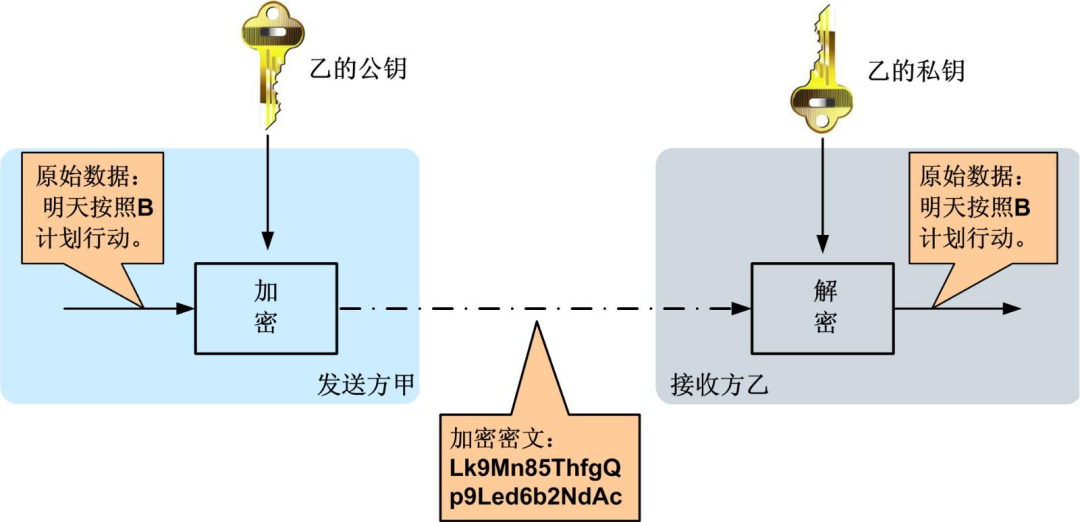
非對稱加密算法，需要用到兩個密鑰：公鑰和私鑰。它們倆是一對的，公鑰負責加密數據，私鑰負責解密數據。

非對稱加密的好處是，公鑰是公開的，任何人都可以使用公鑰加密數據，但只有私鑰能解密，只要張三牢牢握住私鑰，任何人都不能解密出數據。

于是他又開始設計起作弊的流程步驟：

(1) 張三在考場的黑板上寫上：(((x*y)%1000)*m)%1000，x為三位數，y=91，y是公鑰：取x和y的乘積的后三位數，再乘以m，取后三位數

• 李四用公鑰加密答案，傳給張三
• 張三拿到加密后的數據后，用m=11解密數據

注：舉個例子，假如題目正確答案是111，則111乘以91=10101，取后三位101*11=1111，再取后三位得111，就能還原出答案，這是因為91*11=1001，任何一個三位數乘以1001的后三位數都不會改變。之所以用y=91加密，卻可以用m=11解密就是這個道理。

有了非對稱加密，李四、王五和其他同學，都可以使用y=91(公鑰)加密答案，由于m=11(私鑰)只有張三知道，所以也只有他能解密還原出答案。

整個過程，張三不需要向任何人傳遞密鑰，自然也就沒有泄露的風險，密鑰只需要一對(一個公鑰和一個私鑰)，管理起來也相當方面。

設計完作弊方案后，張三激動地告訴了李四。學霸李四聽后點了點頭，但隨即他又提出了一個問題：

比起對稱加密，非對稱加密的安全性是高了很多，但計算也更麻煩了，以前只是計算x+y=z，現在變成計算(((x*y)%1000)*m)%1000。

這樣一來，當李四把答案傳給張三后，張三要拼命地解密，可能考試結束了，都解不完。

這可怎么辦才好?

不甘心的張三又回去想辦法了……

(未完待續...)