搞懂二叉堆的那些事
1. 什么是二叉堆?
“二叉”自不必多說,本章主要介紹的樹都是二叉樹。那么啥是“堆”呢?
我們?cè)谌粘I钪校ǔ?huì)說“一堆東西”或者“堆東西”,這里的“堆”,通常指重疊放置的許多東西。
一堆東西
我們?cè)诙褨|西的時(shí)候,肯定都有一個(gè)經(jīng)驗(yàn),即:為了使這堆東西更穩(wěn)定,會(huì)將比較重的、大的東西放在下面,比較輕的、小的東西放在上面。
這個(gè)經(jīng)驗(yàn)放在數(shù)據(jù)結(jié)構(gòu)——二叉樹中,同樣適用。只不過“重”“大”是根據(jù)結(jié)點(diǎn)值的大小來判斷的,并且是在雙親結(jié)點(diǎn)和孩子結(jié)點(diǎn)之間進(jìn)行比較的。
比如,結(jié)點(diǎn)值大的,作為孩子結(jié)點(diǎn);結(jié)點(diǎn)值小的,作為雙親結(jié)點(diǎn)。
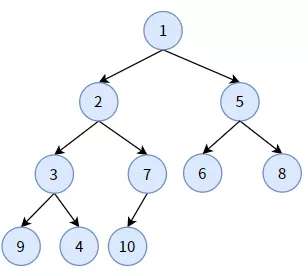
下面舉一個(gè)例子,先看下面一顆普通二叉樹,也是一顆完全二叉樹:
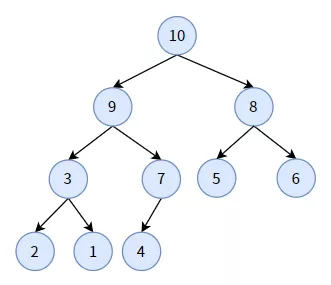
再看下面一顆二叉堆:
最小堆
這個(gè)二叉堆的特點(diǎn)是:
- 它是一顆完全二叉樹。事實(shí)上,該二叉堆就是由上圖的完全二叉樹經(jīng)過調(diào)整轉(zhuǎn)化而來;
- 任何一個(gè)雙親結(jié)點(diǎn)的值,均小于或等于左孩子和右孩子的值;
- 每條分支從根結(jié)點(diǎn)開始都是升序排序(如分支 1-2-3-4)。
這樣的二叉堆被稱為最小堆,它的堆頂,即根結(jié)點(diǎn) A,是整棵樹的最小值。
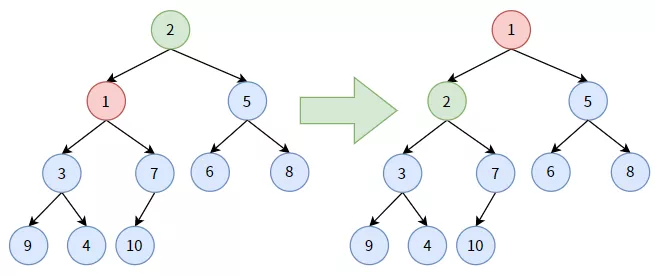
與最小堆相對(duì)應(yīng)的是最大堆:
- 最大堆是一顆完全二叉樹;
- 它的任何一個(gè)雙親結(jié)點(diǎn)的值,均大于或等于左孩子和右孩子的值;
- 每條分支從根結(jié)點(diǎn)開始都是降序排序。
最大堆的堆頂,是整棵樹的最大值。
我們將上圖中的普通二叉樹轉(zhuǎn)化為最大堆,如下圖:
最大堆
2. 二叉堆的操作
2.1. 構(gòu)造二叉堆
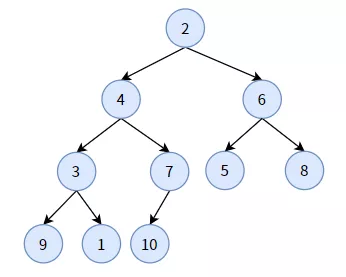
給你一顆完全二叉樹,如何調(diào)整結(jié)點(diǎn),構(gòu)造出一個(gè)二叉堆?下面是一顆無序的完全二叉樹:
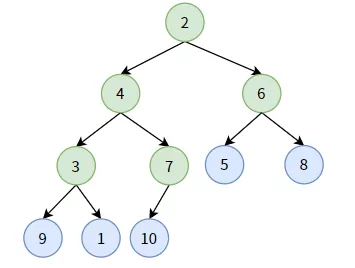
現(xiàn)在我們想要構(gòu)造出一個(gè)最小堆,首先找到這顆完全二叉樹中所有的非葉子結(jié)點(diǎn)(綠色標(biāo)記):
我們要做的事是:對(duì)每個(gè)非葉子結(jié)點(diǎn),做最小堆的“下沉”調(diào)整。
何謂最小堆的“下沉”調(diào)整?
對(duì)某個(gè)非葉子結(jié)點(diǎn),如果該結(jié)點(diǎn)大于其孩子結(jié)點(diǎn)中最小的那個(gè),則交換二者位置,否則不用交換。在圖上則表現(xiàn)出非葉子結(jié)點(diǎn)(即大值結(jié)點(diǎn))“下沉”一個(gè)層次。運(yùn)動(dòng)是相對(duì)的,大值結(jié)點(diǎn)“下沉”,就相當(dāng)于小值結(jié)點(diǎn)“上浮”。
需要注意的是,有時(shí)下沉一次是不夠的,我們需要下沉多次,確保該結(jié)點(diǎn)下沉到底(即它不再大于其孩子)。
所有非葉子結(jié)點(diǎn),從最后一個(gè)開始,按照從右到左,從下到上的順序進(jìn)行多次最小堆的下沉調(diào)整,即可構(gòu)造成最小堆。
比如對(duì)于值為 4 的非葉子結(jié)點(diǎn)而言,它下沉到第 3 層次后,仍然大于其孩子,這不算“下沉到底”,還需要繼續(xù)下沉到第 4 層次。至此,在分支 2-4-3-1 上,“大值”結(jié)點(diǎn) 4 算是下沉到底了。
下面進(jìn)行分步解釋:
1.對(duì)非葉子結(jié)點(diǎn) 7,它小于其孩子結(jié)點(diǎn) 10, 不用“下沉”;
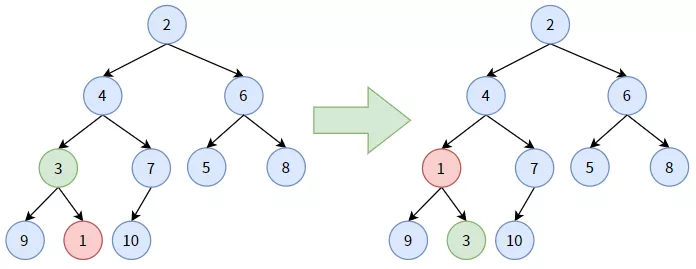
2.對(duì)非葉子結(jié)點(diǎn) 3,它大于其孩子結(jié)點(diǎn)中較大的結(jié)點(diǎn) 1,結(jié)點(diǎn) 3 要“下沉”,和結(jié)點(diǎn) 1 交換。顯然,結(jié)點(diǎn) 3 沉到底了。
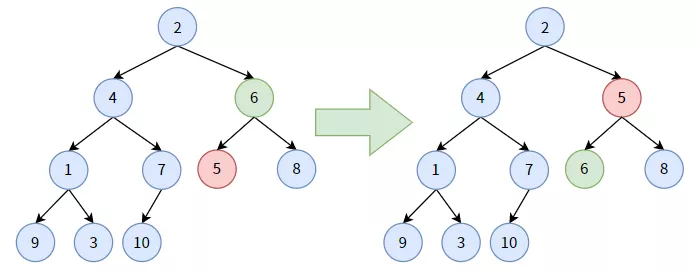
3.對(duì)非葉子結(jié)點(diǎn) 6,它大于其孩子結(jié)點(diǎn)中較小的結(jié)點(diǎn) 5,結(jié)點(diǎn) 6 要“下沉”, 和結(jié)點(diǎn) 5 交換位置。顯然,結(jié)點(diǎn) 6 沉到底了。
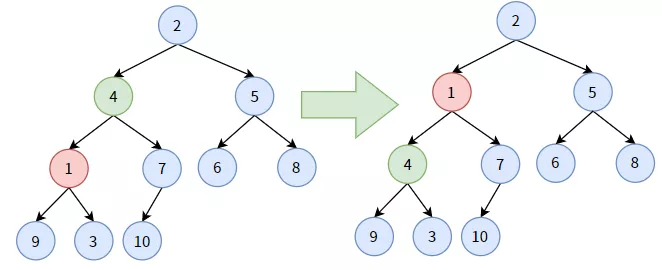
4.對(duì)非葉子結(jié)點(diǎn) 4,它大于其孩子結(jié)點(diǎn)中最小的結(jié)點(diǎn) 1,結(jié)點(diǎn) 4 要 “下沉”,和結(jié)點(diǎn) 1 交換位置。顯然,結(jié)點(diǎn) 4 并未沉到底。
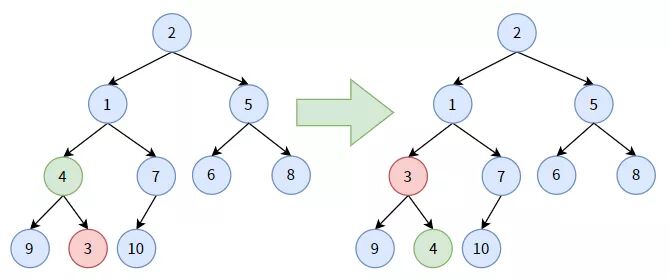
5.仍對(duì)結(jié)點(diǎn) 4,它大于其孩子結(jié)點(diǎn)中最小的結(jié)點(diǎn) 3,結(jié)點(diǎn) 4 要“下沉”, 和結(jié)點(diǎn) 3 交換位置。此時(shí),結(jié)點(diǎn) 4 算是沉底了。
6.對(duì)非葉子結(jié)點(diǎn) 2,它大于其孩子結(jié)點(diǎn)中最小的結(jié)點(diǎn) 1,結(jié)點(diǎn) 2 要“下沉”,和結(jié)點(diǎn) 1 交換位置。顯然,結(jié)點(diǎn) 2 算是沉到底了。
至此,我們將一顆無序的完全二叉樹調(diào)整改造成了最小二叉堆,你可以檢查一下,最小堆中的所有結(jié)點(diǎn)皆滿足雙親的值小于孩子的值。并且,5 條分支上都是有序的。
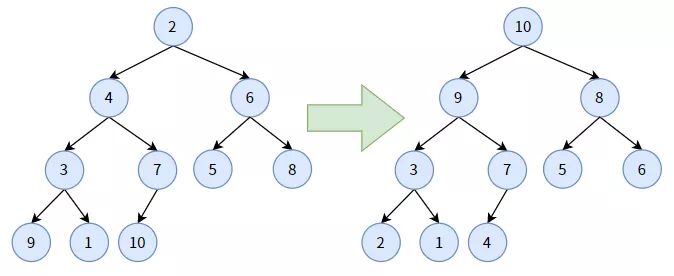
構(gòu)造最大堆的步驟類似,不過最大堆的下沉調(diào)整是:如果某結(jié)點(diǎn)小于其孩子結(jié)點(diǎn)中最大的那個(gè),則交換二者位置,在圖上表現(xiàn)為非葉子結(jié)點(diǎn)(即小值結(jié)點(diǎn))“下沉”一個(gè)層次。通過多次下沉調(diào)整,使該結(jié)點(diǎn)不再小于其孩子。
下圖把一個(gè)無序完全二叉樹調(diào)成為最大堆:
2.2. 插入結(jié)點(diǎn)
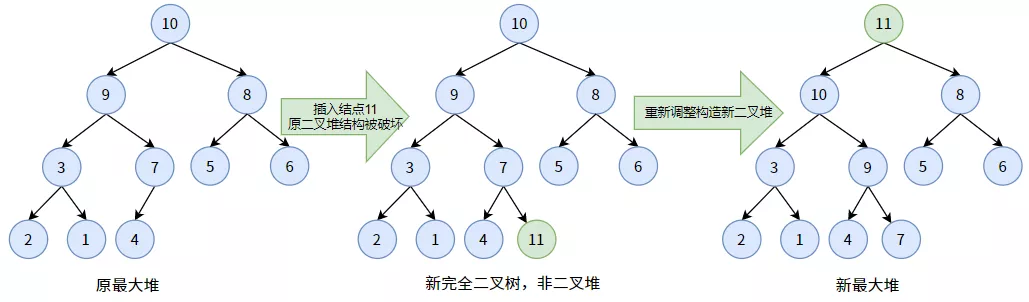
二叉堆是一個(gè)完全二叉樹,要向其中插入結(jié)點(diǎn),插入到完全二叉樹的最后一個(gè)結(jié)點(diǎn)的下一個(gè)位置即可。
比如向下面的一個(gè)最大堆中插入結(jié)點(diǎn) 11,要插到最后一個(gè)結(jié)點(diǎn) 4 的下一個(gè)位置。當(dāng)最大堆新插入一個(gè)結(jié)點(diǎn) 11 時(shí),它就不再是最大堆了,因?yàn)榻Y(jié)點(diǎn) 11 破壞了原堆的結(jié)構(gòu)。所以,我們應(yīng)當(dāng)將其看作一個(gè)新的完全二叉樹,然后調(diào)整新完全二叉樹再次構(gòu)造出最大堆。(調(diào)整過程見上)
插入過程
2.3. 刪除結(jié)點(diǎn)
刪除操作與插入操作相反,是刪除第一個(gè)位置的元素,即刪除堆頂。
我們以刪除上圖最大堆的堆頂 11 為例。
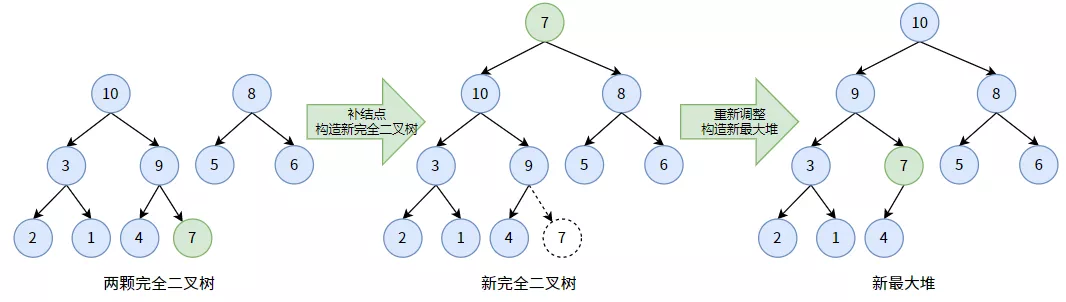
當(dāng)刪除堆頂 11 后,二叉堆原結(jié)構(gòu)被破壞,甚至不是一顆二叉樹了(變成兩顆):
為了保持完全二叉樹的形態(tài),我們把最后一個(gè)結(jié)點(diǎn) 7 補(bǔ)到根結(jié)點(diǎn)去,頂替被刪除的根結(jié)點(diǎn) 11。如此一來,我們又得到了一個(gè)新完全二叉樹(不是二叉堆),然后我們根據(jù)這顆新完全二叉樹再次構(gòu)造出最大堆即可。
刪除過程
3. 二叉堆的存儲(chǔ)結(jié)構(gòu)
二叉堆的存儲(chǔ)結(jié)構(gòu)是順序存儲(chǔ),因?yàn)槎娑咽且活w完全二叉樹,在文章【二叉樹的存儲(chǔ)】中我們說過:完全二叉樹適合使用順序存儲(chǔ)結(jié)構(gòu)來實(shí)現(xiàn)。
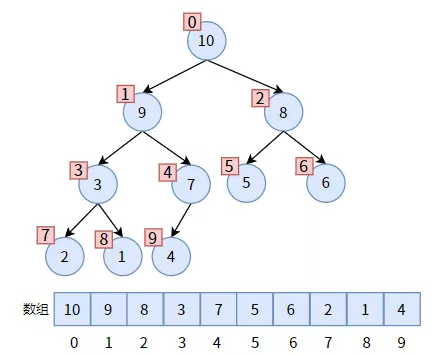
下圖是一個(gè)最大堆,紅色方框是對(duì)結(jié)點(diǎn)的編號(hào),和數(shù)組下標(biāo)一一對(duì)應(yīng)。
二叉堆的順序存儲(chǔ)
鏈?zhǔn)酱鎯?chǔ)結(jié)構(gòu)能夠清晰而形象地為我們展現(xiàn)出二叉堆中雙親結(jié)點(diǎn)和左右孩子的關(guān)系。但是數(shù)組中沒有指針,只有數(shù)組下標(biāo),怎么表示雙親和孩子的關(guān)系呢?
其實(shí)對(duì)于完全二叉樹來說,數(shù)組下標(biāo)足矣!
現(xiàn)假設(shè)二叉堆中雙親結(jié)點(diǎn)的數(shù)組下標(biāo)為 parent_index,左孩子的數(shù)組下標(biāo)為 left_child_index,右孩子的數(shù)組下標(biāo)為 right_child_index,那么它們之間有如下關(guān)系:
(一)left_child_index = 2 × parent_index + 1
(二)right_child_index = 2 × parent_index + 2
(三)parent_index = (left_child_index - 1) ÷ 2
(四)parent_index = (right_child_index - 2) ÷ 2
(五)right_child_index = left_child_index + 1
比如:結(jié)點(diǎn) 3 的下標(biāo)為 3 ,則其左孩子 2 的下標(biāo)為 2 × 3 + 1 = 7、右孩子 1 的下標(biāo)為 2 × 3 + 2 = 8;
結(jié)點(diǎn) 3 的下標(biāo)為 3,作為左孩子,其雙親下標(biāo)為 (3 - 1) ÷ 2 = 1;結(jié)點(diǎn) 7 的下標(biāo)為 4,作為右孩子,其雙親下標(biāo)為 (4 - 2) ÷ 2 = 1;
假設(shè)某結(jié)點(diǎn)的數(shù)組下標(biāo)為 child_index,你不知道該結(jié)點(diǎn)是左孩子還是右孩子,要求其雙親的下標(biāo),有
(六)parent_index = (child_index - 1) ÷ 2
比如:你不知道結(jié)點(diǎn) 5(下標(biāo)為 5)、結(jié)點(diǎn) 6(下標(biāo)為 6)是左孩子還是右孩子,則結(jié)點(diǎn) 5 和結(jié)點(diǎn) 6 的雙親下標(biāo)分別為 (5 - 1) ÷ 2 = 2 、(6 - 1) ÷ 2 = 2。(注意,編程語言中的整型運(yùn)算,所以結(jié)果不是小數(shù))
這里,我們使用結(jié)構(gòu)體實(shí)現(xiàn)二叉堆:
- #define MAXSIZE 20 // 數(shù)組的最大存儲(chǔ)空間
- typedef struct {
- int array[MAXSIZE]; // 存儲(chǔ)數(shù)組
- int length; // 當(dāng)前堆長度(結(jié)點(diǎn)數(shù))
- } BinaryHeap;
在進(jìn)行實(shí)際操作之前,需要初始化二叉堆,即對(duì)數(shù)組及堆長度賦值:
- /**
- * @description: 初始化二叉堆
- * @param {BinaryHeap} *heap 二叉堆
- * @param {int} *array 數(shù)組首地址,該數(shù)組是一個(gè)無序完全二叉樹
- * @param {int} arr_length 數(shù)組長度
- * @return {*} 無
- */
- void init_heap(BinaryHeap *heap, int *array, int arr_length)
- {
- // array 拷貝到 heap 中
- memcpy(heap->array, array, arr_length * sizeof(int));
- // 設(shè)置堆長度
- heap->length = arr_length;
- }
4. 二叉堆的具體實(shí)現(xiàn)
4.1. 調(diào)整和構(gòu)造
這里以構(gòu)造最小堆為例。
要構(gòu)造一個(gè)最小堆,就得調(diào)整所有的非葉子結(jié)點(diǎn)。而調(diào)整的依據(jù)就是比較非葉子結(jié)點(diǎn)和其孩子的大小。
我們約定 parent 為非葉子結(jié)點(diǎn), parent_index 為其下標(biāo)。child 為其孩子中較小的那個(gè),child_index為其下標(biāo)。
child 開始默認(rèn)標(biāo)識(shí)左孩子,那么右孩子的下標(biāo)即為 child_index + 1。當(dāng)左孩子小于等于右孩子時(shí),child 不需要改變;當(dāng)左孩子大于右孩子時(shí),就得更新 child_index ,使child 標(biāo)識(shí)右孩子。
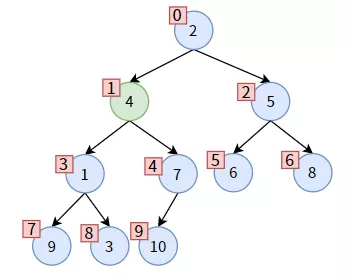
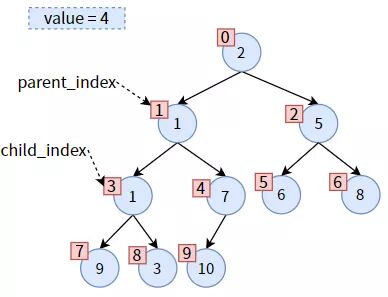
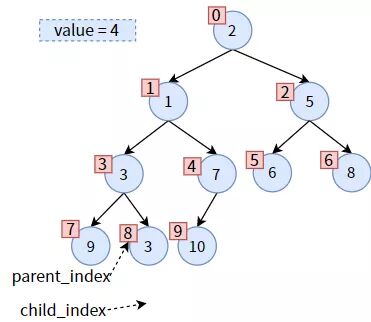
下面結(jié)合下圖中值為 4 的非葉子結(jié)點(diǎn)為例,講述代碼如何實(shí)現(xiàn)。
先比較 parent 的左右孩子,左孩子較小,則 child 為左孩子,不需要更新 child_index。
parent 和 child 各就各位,發(fā)現(xiàn) parent 大于 child,可以交換位置。在交換之前,先保存一下 parent 的值,即 parent_value = 4:
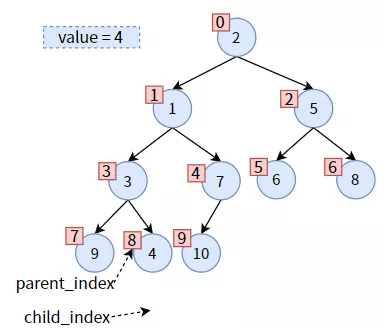
交換位置:先把 child的值賦給 parent,從而達(dá)到 值1 上浮的效果:
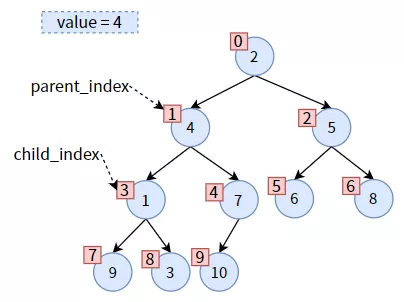
然后更新 parent_index 和 child_index,二者都往下走一層次:
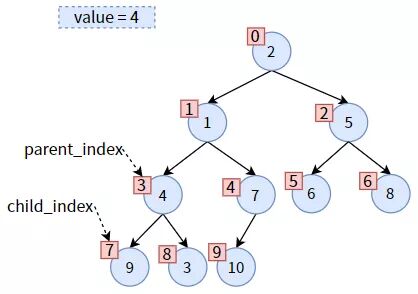
然后將之前保存的 value 賦給現(xiàn)在的 parent,從而達(dá)到 值4 下沉的效果:
一次調(diào)整完成,但對(duì)于 值4 來說,并沒有結(jié)束,因?yàn)?值4 還沒有沉到底。
比較此時(shí) parent 的左右孩子,發(fā)現(xiàn)右孩子較小,則 child 為右子樹,需要更新 child_index,使 child 標(biāo)識(shí)右孩子:
現(xiàn)在可以交換位置了,把 child 的值賦給 parent,達(dá)到 值3 的上浮:

然后,更新 parent_index 和 child_index 的值,二者向下走一個(gè)層次:
把 value 賦給 parent,達(dá)到 值4 的下沉:
此時(shí),child_index 已超過了二叉堆的長度,即 值4 已經(jīng)到底了。
調(diào)整代碼如下:
- /**
- * @description: 針對(duì)某個(gè)非葉子結(jié)點(diǎn)進(jìn)行到底的下沉調(diào)整
- * @param {BinaryHeap} *heap 二叉堆(無序)
- * @param {int} parent_index 某個(gè)非葉子結(jié)點(diǎn)
- * @return {*} 無
- */
- void adjust_for_min_heap(BinaryHeap *heap, int parent_index)
- {
- // value 保存非葉子結(jié)點(diǎn)的值
- int value = heap->array[parent_index];
- // child_index 標(biāo)識(shí)左孩子
- int child_index = parent_index * 2 + 1;
- // 最后一個(gè)結(jié)點(diǎn)的下標(biāo)
- int last_child_index = heap->length - 1;
- // 雙親結(jié)點(diǎn) parent 至少有一個(gè)孩子
- while (child_index <= last_child_index) {
- // 如果雙親結(jié)點(diǎn) parent 有左孩子和右孩子
- if (child_index < last_child_index) {
- // 比較左孩子和右孩子誰小,如果右孩子小,
- if (heap->array[child_index] > heap->array[child_index + 1]) {
- // 則 child_index 標(biāo)識(shí)右孩子
- child_index = child_index + 1;
- }
- }
- // 如果雙親的值大于 child 的值
- if (value > heap->array[child_index]) {
- heap->array[parent_index] = heap->array[child_index]; // 小節(jié)點(diǎn)上浮
- parent_index = child_index; // 更新雙親下標(biāo)
- child_index = parent_index * 2 + 1; // 更新孩子下標(biāo)
- } else { // 不做操作,跳出循環(huán)
- break;
- }
- // 大節(jié)點(diǎn)下沉
- heap->array[parent_index] = value;
- }
- }
構(gòu)造代碼如下:
- /**
- * @description: 構(gòu)造最小堆
- * @param {BinaryHeap} *heap 二叉堆(無序)
- * @return {*} 無
- */
- void create_min_heap(BinaryHeap *heap)
- {
- // 每個(gè)非葉子結(jié)點(diǎn)都調(diào)整
- for (int i = (heap->length - 2) / 2; i >= 0; i--) {
- adjust_for_min_heap(heap, i);
- }
- }
4.2. 插入結(jié)點(diǎn)
只需將新結(jié)點(diǎn)插入二叉堆最后一個(gè)結(jié)點(diǎn)的下一個(gè)位置,然后重新構(gòu)造二叉堆。
以最小堆為例,代碼如下:
- /**
- * @description: 向最小堆中插入一個(gè)元素
- * @param {BinaryHeap} *heap 最小堆指針
- * @param {int} elem 新元素
- * @return {*} 無
- */
- void insert_into_min_heap(BinaryHeap *heap, int elem)
- {
- if (heap->length == MAXSIZE) {
- printf("二叉堆已滿,無法插入。\n");
- return;
- }
- heap->array[heap->length] = elem; // 插入
- heap->length++; // 更新長度
- create_min_heap(heap); // 重新構(gòu)造
- }
4.3. 刪除結(jié)點(diǎn)
將最后一個(gè)結(jié)點(diǎn)移動(dòng)(賦值)到堆頂,然后重新構(gòu)造二叉堆。
以最小堆為例,代碼如下:
- /**
- * @description: 刪除最小堆的堆頂
- * @param {BinaryHeap} *heap 最小堆指針
- * @param {int} *elem 保存變量指針
- * @return {*} 無
- */
- void delete_from_min_heap(BinaryHeap *heap, int *elem)
- {
- if (heap->length == 0) {
- printf("二叉堆空,無元素可刪。\n");
- return;
- }
- *elem = heap->array[0];
- heap->array[0] = heap->array[heap->length - 1]; // 移動(dòng)到堆頂
- heap->length--; // 更新長度
- create_min_heap(heap); //重新構(gòu)造
- }
5. 總結(jié)
構(gòu)造最大堆的本質(zhì)是:將每顆子樹的“大”結(jié)點(diǎn)上浮作為雙親,“小”結(jié)點(diǎn)下沉作為孩子。
構(gòu)造最小堆的本質(zhì)是:將每顆子樹的“小”結(jié)點(diǎn)上浮作為雙親,“大”結(jié)點(diǎn)下沉作為孩子。
插入結(jié)點(diǎn)的本質(zhì)是:插入新結(jié)點(diǎn)至二叉堆末尾,破壞了原二叉堆的結(jié)構(gòu),然后調(diào)整新得到的完全二叉樹,重新構(gòu)造二叉堆。
刪除結(jié)點(diǎn)的本質(zhì)是:刪除堆頂,破壞了原完全二叉樹的結(jié)構(gòu),然后使用最后一個(gè)結(jié)點(diǎn),重新構(gòu)造完全二叉樹,再調(diào)整新得到的完全二叉樹,重新構(gòu)造二叉堆。
用四個(gè)字概括就是——破而后立。
至于代碼實(shí)現(xiàn),關(guān)鍵在于結(jié)點(diǎn)的調(diào)整,把這個(gè)搞明白,剩下的就簡單了。
以上就是二叉堆的原理和相關(guān)操作。
完整代碼請(qǐng)移步至 GitHub[1] | Gitee[2] 獲取。
參考資料
[1]GitHub: https://github.com/xingrenguanxue/Simple-DS-and-Easy-Algo
[2]Gitee: https://gitee.com/xingrenguanxue/Simple-DS-and-Easy-Algo