[[394858]]

 梯度下降是一種優化算法，遵循目標函數的負梯度以定位函數的最小值。

梯度下降的局限性在于，如果梯度變為平坦或大曲率，搜索的進度可能會減慢。可以將動量添加到梯度下降中，該下降合并了一些慣性以進行更新。可以通過合并預計的新位置而非當前位置的梯度(稱為Nesterov的加速梯度(NAG)或Nesterov動量)來進一步改善此效果。

梯度下降的另一個限制是，所有輸入變量都使用單個步長(學習率)。對梯度下降的擴展，如自適應運動估計(Adam)算法，該算法對每個輸入變量使用單獨的步長，但可能會導致步長迅速減小到非常小的值。Nesterov加速的自適應矩估計或Nadam是Adam算法的擴展，該算法結合了Nesterov動量，可以使優化算法具有更好的性能。

在本教程中，您將發現如何從頭開始使用Nadam進行梯度下降優化。完成本教程后，您將知道：

• 梯度下降是一種優化算法，它使用目標函數的梯度來導航搜索空間。
• 納丹(Nadam)是亞當(Adam)版本的梯度下降的擴展，其中包括了內斯特羅夫的動量。
• 如何從頭開始實現Nadam優化算法并將其應用于目標函數并評估結果。

教程概述

本教程分為三個部分：他們是：

• 梯度下降
• Nadam優化算法
• 娜達姆(Nadam)的梯度下降
  • 二維測試問題
  • Nadam的梯度下降優化
  • 可視化的Nadam優化

梯度下降

梯度下降是一種優化算法。它在技術上稱為一階優化算法，因為它明確利用了目標目標函數的一階導數。

一階導數，或簡稱為“導數”，是目標函數在特定點(例如，點)上的變化率或斜率。用于特定輸入。

如果目標函數采用多個輸入變量，則將其稱為多元函數，并且可以將輸入變量視為向量。反過來，多元目標函數的導數也可以視為向量，通常稱為梯度。

梯度：多元目標函數的一階導數。

對于特定輸入，導數或梯度指向目標函數最陡峭的上升方向。梯度下降是指一種最小化優化算法，該算法遵循目標函數的下坡梯度負值來定位函數的最小值。

梯度下降算法需要一個正在優化的目標函數和該目標函數的導數函數。目標函數f()返回給定輸入集合的分數，導數函數f'()給出給定輸入集合的目標函數的導數。梯度下降算法需要問題中的起點(x)，例如輸入空間中的隨機選擇點。

假設我們正在最小化目標函數，然后計算導數并在輸入空間中采取一步，這將導致目標函數下坡運動。首先通過計算輸入空間中要移動多遠的距離來進行下坡運動，計算方法是將步長(稱為alpha或學習率)乘以梯度。然后從當前點減去該值，以確保我們逆梯度移動或向下移動目標函數。

x(t)= x(t-1)–step* f'(x(t)) 

在給定點的目標函數越陡峭，梯度的大小越大，反過來，在搜索空間中采取的步伐也越大。使用步長超參數來縮放步長的大小。

步長：超參數，用于控制算法每次迭代相對于梯度在搜索空間中移動多遠。

如果步長太小，則搜索空間中的移動將很小，并且搜索將花費很長時間。如果步長太大，則搜索可能會在搜索空間附近反彈并跳過最優值。

現在我們已經熟悉了梯度下降優化算法，接下來讓我們看一下Nadam算法。

Nadam優化算法

Nesterov加速的自適應動量估計或Nadam算法是對自適應運動估計(Adam)優化算法的擴展，添加了Nesterov的加速梯度(NAG)或Nesterov動量，這是一種改進的動量。更廣泛地講，Nadam算法是對梯度下降優化算法的擴展。Timothy Dozat在2016年的論文“將Nesterov動量整合到Adam中”中描述了該算法。盡管論文的一個版本是在2015年以同名斯坦福項目報告的形式編寫的。動量將梯度的指數衰減移動平均值(第一矩)添加到梯度下降算法中。這具有消除嘈雜的目標函數和提高收斂性的影響。Adam是梯度下降的擴展，它增加了梯度的第一和第二矩，并針對正在優化的每個參數自動調整學習率。NAG是動量的擴展，其中動量的更新是使用對參數的預計更新量而不是實際當前變量值的梯度來執行的。在某些情況下，這樣做的效果是在找到最佳位置時減慢了搜索速度，而不是過沖。

納丹(Nadam)是對亞當(Adam)的擴展，它使用NAG動量代替經典動量。讓我們逐步介紹該算法的每個元素。Nadam使用衰減步長(alpha)和一階矩(mu)超參數來改善性能。為了簡單起見，我們暫時將忽略此方面，并采用恒定值。首先，對于搜索中要優化的每個參數，我們必須保持梯度的第一矩和第二矩，分別稱為m和n。在搜索開始時將它們初始化為0.0。

• m = 0
• n = 0

該算法在從t = 1開始的時間t內迭代執行，并且每次迭代都涉及計算一組新的參數值x，例如。從x(t-1)到x(t)。如果我們專注于更新一個參數，這可能很容易理解該算法，該算法概括為通過矢量運算來更新所有參數。首先，計算當前時間步長的梯度(偏導數)。

g(t)= f'(x(t-1)) 

接下來，使用梯度和超參數“ mu”更新第一時刻。

m（t）=mu* m（t-1）+（1 –mu）* g（t） 

然后使用“ nu”超參數更新第二時刻。

n（t）= nu * n（t-1）+（1 – nu）* g（t）^ 2 

接下來，使用Nesterov動量對第一時刻進行偏差校正。

mhat =（mu * m（t）/（1 – mu））+（（1 – mu）* g（t）/（1 – mu）） 

然后對第二個時刻進行偏差校正。注意：偏差校正是Adam的一個方面，它與在搜索開始時將第一時刻和第二時刻初始化為零這一事實相反。

nhat = nu * n（t）/（1 – nu） 

最后，我們可以為該迭代計算參數的值。

x（t）= x（t-1）– alpha /（sqrt（nhat）+ eps）* mhat 

其中alpha是步長(學習率)超參數，sqrt()是平方根函數，eps(epsilon)是一個較小的值，如1e-8，以避免除以零誤差。

回顧一下，該算法有三個超參數。他們是：

alpha：初始步長（學習率），典型值為0.002。 
mu：第一時刻的衰減因子（Adam中的beta1），典型值為0.975。 
nu：第二時刻的衰減因子（Adam中的beta2），典型值為0.999。 

就是這樣。接下來，讓我們看看如何在Python中從頭開始實現該算法。

娜達姆(Nadam)的梯度下降

在本節中，我們將探索如何使用Nadam動量實現梯度下降優化算法。

二維測試問題

首先，讓我們定義一個優化函數。我們將使用一個簡單的二維函數，該函數將每個維的輸入平方，并定義有效輸入的范圍(從-1.0到1.0)。下面的Objective()函數實現了此功能

# objective function 
def objective(x, y): 
 return x**2.0 + y**2.0 

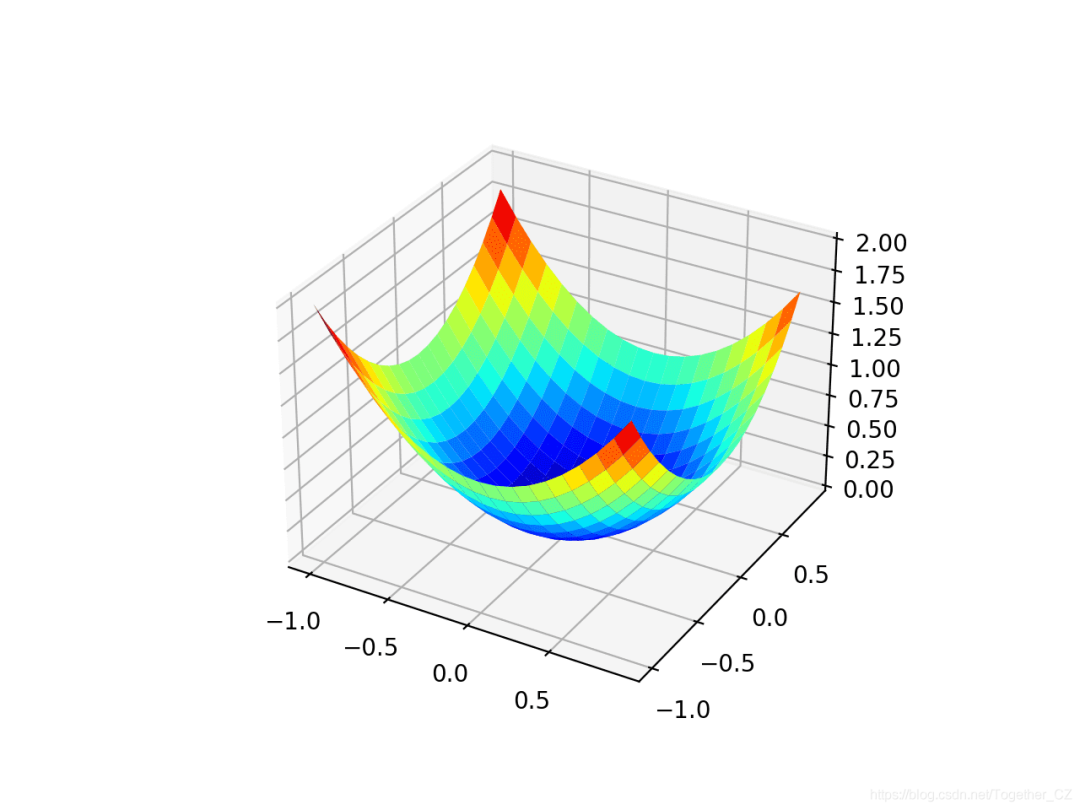
我們可以創建數據集的三維圖，以了解響應面的曲率。下面列出了繪制目標函數的完整示例。

# 3d plot of the test function 
from numpy import arange 
from numpy import meshgrid 
from matplotlib import pyplot 
  
# objective function 
def objective(x, y): 
 return x**2.0 + y**2.0 
  
# define range for input 
r_min, r_max = -1.0, 1.0 
# sample input range uniformly at 0.1 increments 
xaxis = arange(r_min, r_max, 0.1) 
yaxis = arange(r_min, r_max, 0.1) 
# create a mesh from the axis 
x, y = meshgrid(xaxis, yaxis) 
# compute targets 
results = objective(x, y) 
# create a surface plot with the jet color scheme 
figure = pyplot.figure() 
axis = figure.gca(projection='3d') 
axis.plot_surface(x, y, results, cmap='jet') 
# show the plot 
pyplot.show() 

運行示例將創建目標函數的三維表面圖。我們可以看到全局最小值為f(0，0)= 0的熟悉的碗形狀。

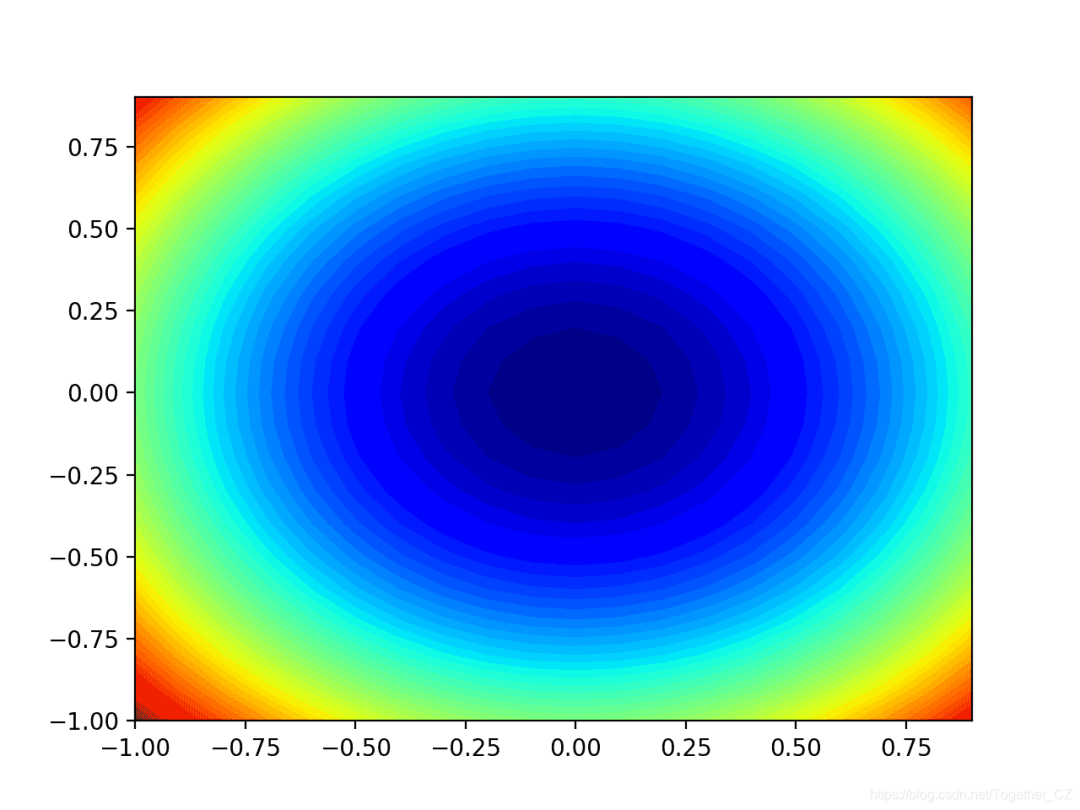
我們還可以創建函數的二維圖。這在以后要繪制搜索進度時會很有幫助。下面的示例創建目標函數的輪廓圖。

# contour plot of the test function 
from numpy import asarray 
from numpy import arange 
from numpy import meshgrid 
from matplotlib import pyplot 
  
# objective function 
def objective(x, y): 
 return x**2.0 + y**2.0 
  
# define range for input 
bounds = asarray([[-1.0, 1.0], [-1.0, 1.0]]) 
# sample input range uniformly at 0.1 increments 
xaxis = arange(bounds[0,0], bounds[0,1], 0.1) 
yaxis = arange(bounds[1,0], bounds[1,1], 0.1) 
# create a mesh from the axis 
x, y = meshgrid(xaxis, yaxis) 
# compute targets 
results = objective(x, y) 
# create a filled contour plot with 50 levels and jet color scheme 
pyplot.contourf(x, y, results, levels=50, cmap='jet') 
# show the plot 
pyplot.show() 

運行示例將創建目標函數的二維輪廓圖。我們可以看到碗的形狀被壓縮為以顏色漸變顯示的輪廓。我們將使用該圖來繪制在搜索過程中探索的特定點。

現在我們有了一個測試目標函數，讓我們看一下如何實現Nadam優化算法。

Nadam的梯度下降優化

我們可以將Nadam的梯度下降應用于測試問題。首先，我們需要一個函數來計算此函數的導數。

x ^ 2的導數在每個維度上均為x * 2。

f（x）= x ^ 2 
f'（x）= x * 2 

derived()函數在下面實現了這一點。

# derivative of objective function 
def derivative(x, y): 
 return asarray([x * 2.0, y * 2.0]) 

接下來，我們可以使用Nadam實現梯度下降優化。首先，我們可以選擇問題范圍內的隨機點作為搜索的起點。假定我們有一個數組，該數組定義搜索范圍，每個維度一行，并且第一列定義最小值，第二列定義維度的最大值。

# generate an initial point 
x = bounds[:, 0] + rand(len(bounds)) * (bounds[:, 1] - bounds[:, 0]) 
score = objective(x[0], x[1]) 

接下來，我們需要初始化力矩矢量。

# initialize decaying moving averages 
m = [0.0 for _ in range(bounds.shape[0])] 
n = [0.0 for _ in range(bounds.shape[0])] 

然后，我們運行由“ n_iter”超參數定義的算法的固定迭代次數。

... 
# run iterations of gradient descent 
for t in range(n_iter): 
 ... 

第一步是計算當前參數集的導數。

... 
# calculate gradient g(t) 
g = derivative(x[0], x[1]) 

接下來，我們需要執行Nadam更新計算。為了提高可讀性，我們將使用命令式編程樣式來一次執行一個變量的這些計算。在實踐中，我建議使用NumPy向量運算以提高效率。

... 
# build a solution one variable at a time 
for i in range(x.shape[0]): 
 ... 

首先，我們需要計算力矩矢量。

# m(t) = mu * m(t-1) + (1 - mu) * g(t) 
m[i] = mu * m[i] + (1.0 - mu) * g[i] 

然后是第二個矩向量。

# nhat = nu * n(t) / (1 - nu) 
nhat = nu * n[i] / (1.0 - nu) 
# n(t) = nu * n(t-1) + (1 - nu) * g(t)^2 
n[i] = nu * n[i] + (1.0 - nu) * g[i]**2 

然后是經過偏差校正的內斯特羅夫動量。

# mhat = (mu * m(t) / (1 - mu)) + ((1 - mu) * g(t) / (1 - mu)) 
mhat = (mu * m[i] / (1.0 - mu)) + ((1 - mu) * g[i] / (1.0 - mu)) 

偏差校正的第二時刻。

# nhat = nu * n(t) / (1 - nu) 
nhat = nu * n[i] / (1.0 - nu) 

最后更新參數。

# x(t) = x(t-1) - alpha / (sqrt(nhat) + eps) * mhat 
x[i] = x[i] - alpha / (sqrt(nhat) + eps) * mhat 

然后，針對要優化的每個參數重復此操作。在迭代結束時，我們可以評估新的參數值并報告搜索的性能。

# evaluate candidate point 
score = objective(x[0], x[1]) 
# report progress 
print('>%d f(%s) = %.5f' % (t, x, score)) 

我們可以將所有這些結合到一個名為nadam()的函數中，該函數采用目標函數和派生函數的名稱以及算法超參數，并返回在搜索及其評估結束時找到的最佳解決方案。

# gradient descent algorithm with nadam 
def nadam(objective, derivative, bounds, n_iter, alpha, mu, nu, eps=1e-8): 
 # generate an initial point 
 x = bounds[:, 0] + rand(len(bounds)) * (bounds[:, 1] - bounds[:, 0]) 
 score = objective(x[0], x[1]) 
 # initialize decaying moving averages 
 m = [0.0 for _ in range(bounds.shape[0])] 
 n = [0.0 for _ in range(bounds.shape[0])] 
 # run the gradient descent 
 for t in range(n_iter): 
  # calculate gradient g(t) 
  g = derivative(x[0], x[1]) 
  # build a solution one variable at a time 
  for i in range(bounds.shape[0]): 
   # m(t) = mu * m(t-1) + (1 - mu) * g(t) 
   m[i] = mu * m[i] + (1.0 - mu) * g[i] 
   # n(t) = nu * n(t-1) + (1 - nu) * g(t)^2 
   n[i] = nu * n[i] + (1.0 - nu) * g[i]**2 
   # mhat = (mu * m(t) / (1 - mu)) + ((1 - mu) * g(t) / (1 - mu)) 
   mhat = (mu * m[i] / (1.0 - mu)) + ((1 - mu) * g[i] / (1.0 - mu)) 
   # nhat = nu * n(t) / (1 - nu) 
   nhat = nu * n[i] / (1.0 - nu) 
   # x(t) = x(t-1) - alpha / (sqrt(nhat) + eps) * mhat 
   x[i] = x[i] - alpha / (sqrt(nhat) + eps) * mhat 
  # evaluate candidate point 
  score = objective(x[0], x[1]) 
  # report progress 
  print('>%d f(%s) = %.5f' % (t, x, score)) 
 return [x, score] 

然后，我們可以定義函數和超參數的界限，并調用函數執行優化。在這種情況下，我們將運行該算法進行50次迭代，初始alpha為0.02，μ為0.8，nu為0.999，這是經過一點點反復試驗后發現的。

# seed the pseudo random number generator 
seed(1) 
# define range for input 
bounds = asarray([[-1.0, 1.0], [-1.0, 1.0]]) 
# define the total iterations 
n_iter = 50 
# steps size 
alpha = 0.02 
# factor for average gradient 
mu = 0.8 
# factor for average squared gradient 
nu = 0.999 
# perform the gradient descent search with nadam 
best, score = nadam(objective, derivative, bounds, n_iter, alpha, mu, nu) 

運行結束時，我們將報告找到的最佳解決方案。

# summarize the result 
print('Done!') 
print('f(%s) = %f' % (best, score)) 

綜合所有這些，下面列出了適用于我們的測試問題的Nadam梯度下降的完整示例。

# gradient descent optimization with nadam for a two-dimensional test function 
from math import sqrt 
from numpy import asarray 
from numpy.random import rand 
from numpy.random import seed 
  
# objective function 
def objective(x, y): 
 return x**2.0 + y**2.0 
  
# derivative of objective function 
def derivative(x, y): 
 return asarray([x * 2.0, y * 2.0]) 
  
# gradient descent algorithm with nadam 
def nadam(objective, derivative, bounds, n_iter, alpha, mu, nu, eps=1e-8): 
 # generate an initial point 
 x = bounds[:, 0] + rand(len(bounds)) * (bounds[:, 1] - bounds[:, 0]) 
 score = objective(x[0], x[1]) 
 # initialize decaying moving averages 
 m = [0.0 for _ in range(bounds.shape[0])] 
 n = [0.0 for _ in range(bounds.shape[0])] 
 # run the gradient descent 
 for t in range(n_iter): 
  # calculate gradient g(t) 
  g = derivative(x[0], x[1]) 
  # build a solution one variable at a time 
  for i in range(bounds.shape[0]): 
   # m(t) = mu * m(t-1) + (1 - mu) * g(t) 
   m[i] = mu * m[i] + (1.0 - mu) * g[i] 
   # n(t) = nu * n(t-1) + (1 - nu) * g(t)^2 
   n[i] = nu * n[i] + (1.0 - nu) * g[i]**2 
   # mhat = (mu * m(t) / (1 - mu)) + ((1 - mu) * g(t) / (1 - mu)) 
   mhat = (mu * m[i] / (1.0 - mu)) + ((1 - mu) * g[i] / (1.0 - mu)) 
   # nhat = nu * n(t) / (1 - nu) 
   nhat = nu * n[i] / (1.0 - nu) 
   # x(t) = x(t-1) - alpha / (sqrt(nhat) + eps) * mhat 
   x[i] = x[i] - alpha / (sqrt(nhat) + eps) * mhat 
  # evaluate candidate point 
  score = objective(x[0], x[1]) 
  # report progress 
  print('>%d f(%s) = %.5f' % (t, x, score)) 
 return [x, score] 
  
# seed the pseudo random number generator 
seed(1) 
# define range for input 
bounds = asarray([[-1.0, 1.0], [-1.0, 1.0]]) 
# define the total iterations 
n_iter = 50 
# steps size 
alpha = 0.02 
# factor for average gradient 
mu = 0.8 
# factor for average squared gradient 
nu = 0.999 
# perform the gradient descent search with nadam 
best, score = nadam(objective, derivative, bounds, n_iter, alpha, mu, nu) 
print('Done!') 
print('f(%s) = %f' % (best, score)) 

運行示例將優化算法和Nadam應用于我們的測試問題，并報告算法每次迭代的搜索性能。

注意：由于算法或評估程序的隨機性，或者數值精度的差異，您的結果可能會有所不同。考慮運行該示例幾次并比較平均結果。

在這種情況下，我們可以看到在大約44次搜索迭代后找到了接近最佳的解決方案，輸入值接近0.0和0.0，評估為0.0。

>40 f([ 5.07445337e-05 -3.32910019e-03]) = 0.00001 
>41 f([-1.84325171e-05 -3.00939427e-03]) = 0.00001 
>42 f([-6.78814472e-05 -2.69839367e-03]) = 0.00001 
>43 f([-9.88339249e-05 -2.40042096e-03]) = 0.00001 
>44 f([-0.00011368 -0.00211861]) = 0.00000 
>45 f([-0.00011547 -0.00185511]) = 0.00000 
>46 f([-0.0001075 -0.00161122]) = 0.00000 
>47 f([-9.29922627e-05 -1.38760991e-03]) = 0.00000 
>48 f([-7.48258406e-05 -1.18436586e-03]) = 0.00000 
>49 f([-5.54299505e-05 -1.00116899e-03]) = 0.00000 
Done! 
f([-5.54299505e-05 -1.00116899e-03]) = 0.000001 

可視化的Nadam優化

我們可以在域的等高線上繪制Nadam搜索的進度。這可以為算法迭代過程中的搜索進度提供直觀的認識。我們必須更新nadam()函數以維護在搜索過程中找到的所有解決方案的列表，然后在搜索結束時返回此列表。下面列出了具有這些更改的功能的更新版本。

# gradient descent algorithm with nadam 
def nadam(objective, derivative, bounds, n_iter, alpha, mu, nu, eps=1e-8): 
 solutions = list() 
 # generate an initial point 
 x = bounds[:, 0] + rand(len(bounds)) * (bounds[:, 1] - bounds[:, 0]) 
 score = objective(x[0], x[1]) 
 # initialize decaying moving averages 
 m = [0.0 for _ in range(bounds.shape[0])] 
 n = [0.0 for _ in range(bounds.shape[0])] 
 # run the gradient descent 
 for t in range(n_iter): 
  # calculate gradient g(t) 
  g = derivative(x[0], x[1]) 
  # build a solution one variable at a time 
  for i in range(bounds.shape[0]): 
   # m(t) = mu * m(t-1) + (1 - mu) * g(t) 
   m[i] = mu * m[i] + (1.0 - mu) * g[i] 
   # n(t) = nu * n(t-1) + (1 - nu) * g(t)^2 
   n[i] = nu * n[i] + (1.0 - nu) * g[i]**2 
   # mhat = (mu * m(t) / (1 - mu)) + ((1 - mu) * g(t) / (1 - mu)) 
   mhat = (mu * m[i] / (1.0 - mu)) + ((1 - mu) * g[i] / (1.0 - mu)) 
   # nhat = nu * n(t) / (1 - nu) 
   nhat = nu * n[i] / (1.0 - nu) 
   # x(t) = x(t-1) - alpha / (sqrt(nhat) + eps) * mhat 
   x[i] = x[i] - alpha / (sqrt(nhat) + eps) * mhat 
  # evaluate candidate point 
  score = objective(x[0], x[1]) 
  # store solution 
  solutions.append(x.copy()) 
  # report progress 
  print('>%d f(%s) = %.5f' % (t, x, score)) 
 return solutions 

然后，我們可以像以前一樣執行搜索，這一次將檢索解決方案列表，而不是最佳的最終解決方案。

# seed the pseudo random number generator 
seed(1) 
# define range for input 
bounds = asarray([[-1.0, 1.0], [-1.0, 1.0]]) 
# define the total iterations 
n_iter = 50 
# steps size 
alpha = 0.02 
# factor for average gradient 
mu = 0.8 
# factor for average squared gradient 
nu = 0.999 
# perform the gradient descent search with nadam 
solutions = nadam(objective, derivative, bounds, n_iter, alpha, mu, nu) 

然后，我們可以像以前一樣創建目標函數的輪廓圖。

# sample input range uniformly at 0.1 increments 
xaxis = arange(bounds[0,0], bounds[0,1], 0.1) 
yaxis = arange(bounds[1,0], bounds[1,1], 0.1) 
# create a mesh from the axis 
x, y = meshgrid(xaxis, yaxis) 
# compute targets 
results = objective(x, y) 
# create a filled contour plot with 50 levels and jet color scheme 
pyplot.contourf(x, y, results, levels=50, cmap='jet') 

最后，我們可以將在搜索過程中找到的每個解決方案繪制成一條由一條線連接的白點。

# plot the sample as black circles 
solutions = asarray(solutions) 
pyplot.plot(solutions[:, 0], solutions[:, 1], '.-', color='w') 

綜上所述，下面列出了對測試問題執行Nadam優化并將結果繪制在輪廓圖上的完整示例。

# example of plotting the nadam search on a contour plot of the test function 
from math import sqrt 
from numpy import asarray 
from numpy import arange 
from numpy import product 
from numpy.random import rand 
from numpy.random import seed 
from numpy import meshgrid 
from matplotlib import pyplot 
from mpl_toolkits.mplot3d import Axes3D 
  
# objective function 
def objective(x, y): 
 return x**2.0 + y**2.0 
  
# derivative of objective function 
def derivative(x, y): 
 return asarray([x * 2.0, y * 2.0]) 
  
# gradient descent algorithm with nadam 
def nadam(objective, derivative, bounds, n_iter, alpha, mu, nu, eps=1e-8): 
 solutions = list() 
 # generate an initial point 
 x = bounds[:, 0] + rand(len(bounds)) * (bounds[:, 1] - bounds[:, 0]) 
 score = objective(x[0], x[1]) 
 # initialize decaying moving averages 
 m = [0.0 for _ in range(bounds.shape[0])] 
 n = [0.0 for _ in range(bounds.shape[0])] 
 # run the gradient descent 
 for t in range(n_iter): 
  # calculate gradient g(t) 
  g = derivative(x[0], x[1]) 
  # build a solution one variable at a time 
  for i in range(bounds.shape[0]): 
   # m(t) = mu * m(t-1) + (1 - mu) * g(t) 
   m[i] = mu * m[i] + (1.0 - mu) * g[i] 
   # n(t) = nu * n(t-1) + (1 - nu) * g(t)^2 
   n[i] = nu * n[i] + (1.0 - nu) * g[i]**2 
   # mhat = (mu * m(t) / (1 - mu)) + ((1 - mu) * g(t) / (1 - mu)) 
   mhat = (mu * m[i] / (1.0 - mu)) + ((1 - mu) * g[i] / (1.0 - mu)) 
   # nhat = nu * n(t) / (1 - nu) 
   nhat = nu * n[i] / (1.0 - nu) 
   # x(t) = x(t-1) - alpha / (sqrt(nhat) + eps) * mhat 
   x[i] = x[i] - alpha / (sqrt(nhat) + eps) * mhat 
  # evaluate candidate point 
  score = objective(x[0], x[1]) 
  # store solution 
  solutions.append(x.copy()) 
  # report progress 
  print('>%d f(%s) = %.5f' % (t, x, score)) 
 return solutions 
  
# seed the pseudo random number generator 
seed(1) 
# define range for input 
bounds = asarray([[-1.0, 1.0], [-1.0, 1.0]]) 
# define the total iterations 
n_iter = 50 
# steps size 
alpha = 0.02 
# factor for average gradient 
mu = 0.8 
# factor for average squared gradient 
nu = 0.999 
# perform the gradient descent search with nadam 
solutions = nadam(objective, derivative, bounds, n_iter, alpha, mu, nu) 
# sample input range uniformly at 0.1 increments 
xaxis = arange(bounds[0,0], bounds[0,1], 0.1) 
yaxis = arange(bounds[1,0], bounds[1,1], 0.1) 
# create a mesh from the axis 
x, y = meshgrid(xaxis, yaxis) 
# compute targets 
results = objective(x, y) 
# create a filled contour plot with 50 levels and jet color scheme 
pyplot.contourf(x, y, results, levels=50, cmap='jet') 
# plot the sample as black circles 
solutions = asarray(solutions) 
pyplot.plot(solutions[:, 0], solutions[:, 1], '.-', color='w') 
# show the plot 
pyplot.show() 

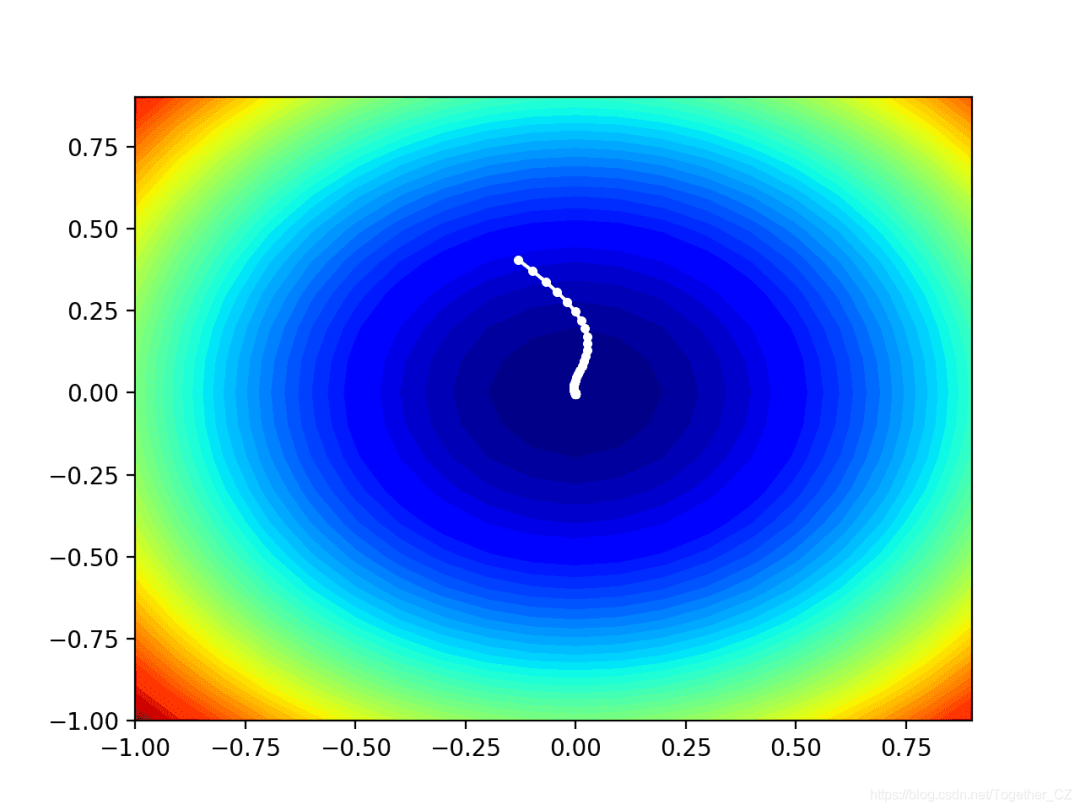
運行示例將像以前一樣執行搜索，但是在這種情況下，將創建目標函數的輪廓圖。

在這種情況下，我們可以看到在搜索過程中找到的每個解決方案都顯示一個白點，從最優點開始，逐漸靠近圖中心的最優點。