[[391530]]

 二叉樹的問題分析

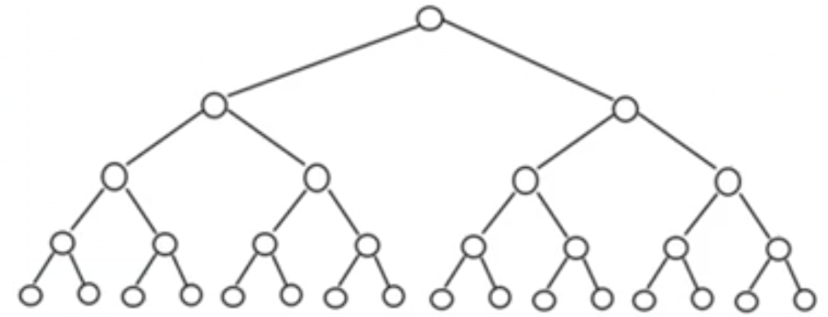
二叉樹的操作效率高，但是也存在問題，請看下面的二叉樹

二叉樹需要加載到內存，如果二叉樹的節點少，沒有什么問題，但是如果二叉樹的節點很多(比如1億)，就存在如下問題：

1. 在構建二叉樹時，需要多次進行I/O操作(海量數據存在數據庫或文件中)，節點海量，構建樹時，速度有影響。
2. 節點海量，也會造成二叉樹的高度很大，會降低操作速度。

多叉樹

1. 在二叉樹中，每個節點有數據項，最多有兩個子節點。如果允許每個節點可以有更多的數據項和更多的節點，就是多叉樹(multiway tree).
2. 如2-3樹，2-3-4樹就是多叉樹，多叉樹通過重新組織節點，減少樹的高度，能對二叉樹進行優化。
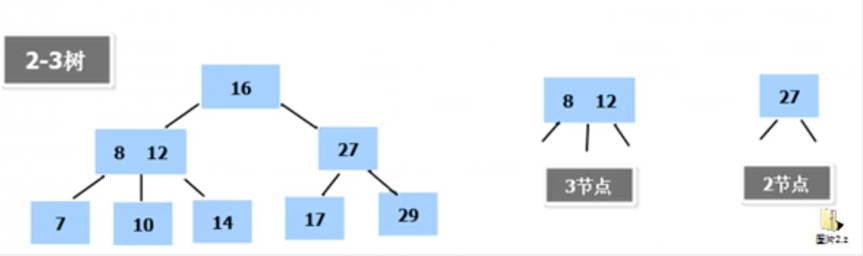
3. 舉例說明(下面的2-3樹)就是一顆多叉樹

B樹的基本介紹

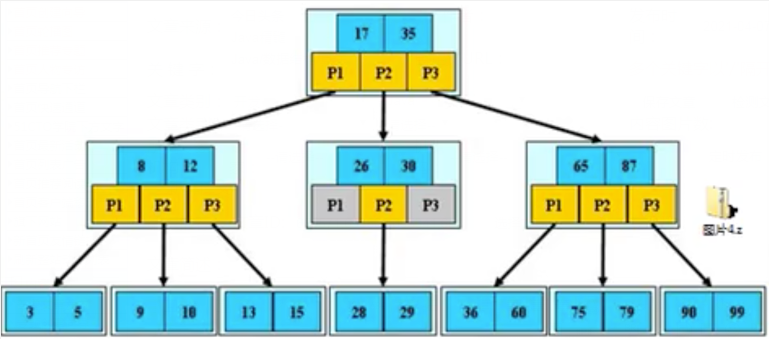
B-Tree 樹即B樹，B即Balanced，平衡的意思。在mysql中說某種類型的索引是基于B樹或者B+樹，如下圖：

B樹說明：

1. B樹的階：節點的最多子節點個數，比如2-3樹的階是3，2-3-4樹的階是4.
2. B樹的搜索：從根節點開始，對節點內的關鍵字(有序)序列進行二分查找，如果命中則結束，否則進入查詢關鍵字所屬范圍的子節點;重復，直到所對應的子指針為空，或已經是葉子節點。
3. 關鍵字集合分布在整棵樹中，即葉子節點和非葉子節點都存放數據。
4. 搜索可能在非葉子節點結束
5. 其搜索性能等價于在關鍵字內全集做一次二分查找。

B樹通過重新組織節點，降低樹的高度，并減少I/O讀寫次數來提升效率。

1. 如圖B樹通過重新組織節點，降低了樹的高度。
2. 文件系統及數據庫系統的設計者利用了磁盤預讀原理，將一個節點的大小設為等于一個頁(頁的大小通常為4k)，這樣每個節點只需一次I/O就可以完全載入。
3. 將樹的度M(樹中某個父節點含有最多子節點的個數)設置為1024，在600億個元素中，最多只需4次I/O操作就可以讀取到想要的元素，B樹廣泛用于文件存儲系統及數據庫系統中。

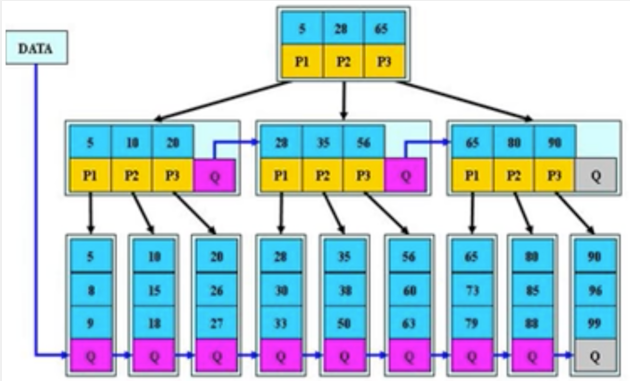
B+樹基本介紹

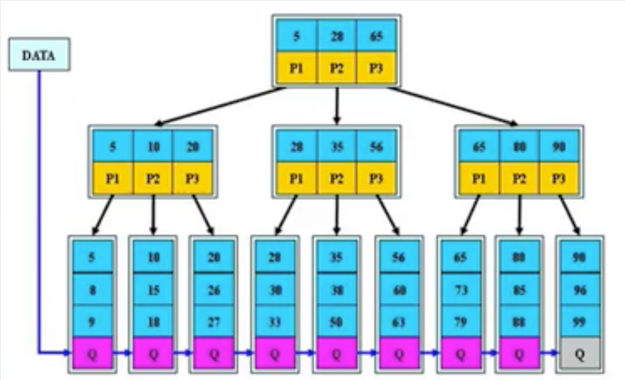
B+樹是B樹的變體，也是一種多路查找樹

B+樹說明：

1. B+樹的搜索與B樹也基本相同，區別是B+樹只有達到葉子節點才能命中(B樹可以在非葉子節點命中)，其性能也等價于在關鍵字全集做一次二分查找。
2. 所有關鍵字出現在葉子節點的鏈表中(即數據只能在葉子節點【也叫稠密索引】)，且鏈表中的關鍵字(數據)恰好是有序的。
3. 不可能在非葉子節點命中。
4. 非葉子節點相當于葉子節點的索引(稀疏索引)，葉子節點相當于是存儲(關鍵字)數據的數據層。
5. 更適合文件索引系統。
6. B樹和B+樹各有自己的場景，不能說B+樹完全比B樹好，反之亦然。

B*樹基本介紹

B* 樹是 B+ 樹的變體，在B+樹的非根和非葉子節點再增加指向兄弟的指針。

B 樹說明：*

1. B*樹定義了非葉子節點關鍵字個數至少為(2/3)*M，即塊的最低使用率為2/3，而B+樹的塊的最低使用率1/2。
2. 從第一個特點可以看出，B*樹分配新節點的概率要比B+樹要低，空間使用率更高。

2-3樹基本介紹(最簡單的B樹)

2-3樹是最簡單的B-樹結構，具有如下特點：

1. 2-3樹的所有葉子節點都在同一層。(只要是B樹都滿足這個條件)
2. 有兩個子節點的節點叫做二節點，二節點要么沒有子節點，要么有兩個子節點。
3. 有三個子節點的節點叫做三節點，三節點要么沒有子節點，要么有三個子節點。
4. 2-3是由二節點和三節點構成的樹。

2-3樹的插入規則：

1. 2-3樹的所有葉子節點都在同一層。(只要是B樹都滿足這個條件)。
2. 有兩個子節點的節點叫做二節點，二節點要么沒有子節點，要么有兩個子節點。
3. 有三個子節點的節點叫做三節點，三節點要么沒有子節點，要么有三個子節點。
4. 當按照規則插入一個數到某個節點時，不能滿足上面三個要求，就需要拆，先向上拆，如果上層滿，則拆本層，拆后仍然需要滿足上面三個條件。
5. 對于三節點的子樹的值大小仍然滿足(BST二叉排序樹)的規則。