本文轉(zhuǎn)自雷鋒網(wǎng)，如需轉(zhuǎn)載請至雷鋒網(wǎng)官網(wǎng)申請授權(quán)。

廣度優(yōu)先搜索、Dijkstra和A*是圖上的三種典型路徑規(guī)劃算法。它們都可用于圖搜索，不同之處在于隊(duì)列和啟發(fā)式函數(shù)兩個(gè)參數(shù)。

本項(xiàng)目探索并可視化不同算法如何根據(jù)選擇參數(shù)進(jìn)行圖搜索。

算法的一般性原理如下：

將邊界初始化為包含起始節(jié)點(diǎn)的隊(duì)列。

當(dāng)邊界隊(duì)列不為空時(shí)，從隊(duì)列中“訪問”并刪除一個(gè)“當(dāng)前”節(jié)點(diǎn)，同時(shí)將訪問節(jié)點(diǎn)的每個(gè)鄰居節(jié)點(diǎn)添加到隊(duì)列，其成本是到達(dá)當(dāng)前節(jié)點(diǎn)的成本加上從當(dāng)前節(jié)點(diǎn)訪問鄰居的成本再加上鄰居節(jié)點(diǎn)和目標(biāo)節(jié)點(diǎn)的啟發(fā)式函數(shù)值。其中，啟發(fā)式函數(shù)是對兩個(gè)節(jié)點(diǎn)的路徑成本的估計(jì)。

存儲訪問路徑（通常存儲在cameFrom圖中），以便后續(xù)重建路徑。如果鄰居節(jié)點(diǎn)已經(jīng)在列表中，同時(shí)新路徑的成本較低，那么更改其成本。

找到目標(biāo)路徑（提前退出）或列表為空時(shí)，停止算法。

BFS

使用先進(jìn)先出隊(duì)列實(shí)現(xiàn)BFS。這種隊(duì)列會(huì)忽略路徑中鏈接的開銷，并根據(jù)跳數(shù)進(jìn)行擴(kuò)展，因此可以確保找到最短路徑的跳數(shù)，而跳數(shù)相關(guān)的成本。啟發(fā)式函數(shù)的選擇是任意的，因?yàn)樵谶@個(gè)過程中其并不起作用。

使用數(shù)組可實(shí)現(xiàn)先進(jìn)先出，即將元素附加到末尾并從頭刪除。

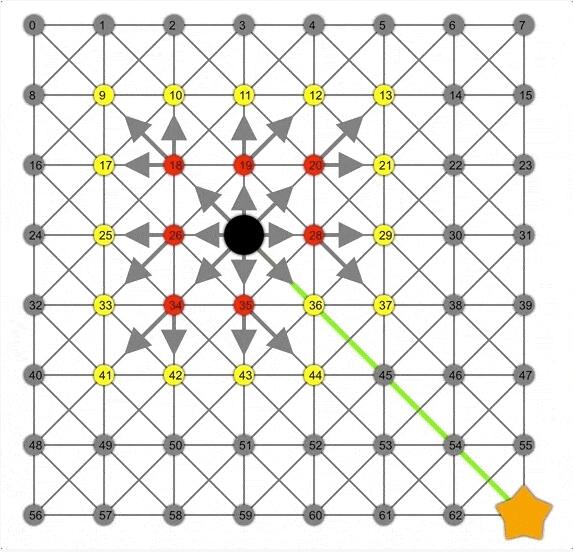
BFS演示動(dòng)圖。注意邊界節(jié)點(diǎn)（黃色）是如何在網(wǎng)格中擴(kuò)展為正方形的。在這里，正方形是相同“跳距”的節(jié)點(diǎn)集。

Dijkstra

在圖上使用優(yōu)先級隊(duì)列和始終返回0的啟發(fā)式函數(shù)，便得到Dijkstra算法。

相比于BFS，Dijkstra最大的不同在于考慮了成本。通過該算法，可以根據(jù)節(jié)點(diǎn)到節(jié)點(diǎn)的成本找到最短路徑。

優(yōu)先級隊(duì)列使用數(shù)組實(shí)現(xiàn)，在每次插入新節(jié)點(diǎn)后對該數(shù)組進(jìn)行排序。盡管實(shí)現(xiàn)優(yōu)先級隊(duì)列還有其他更高效的方式，但在我們的場景中，數(shù)組是足夠快的，而且實(shí)現(xiàn)起來也簡單。

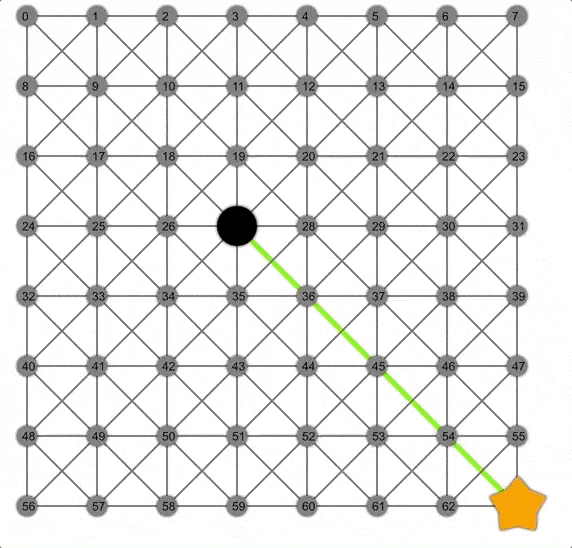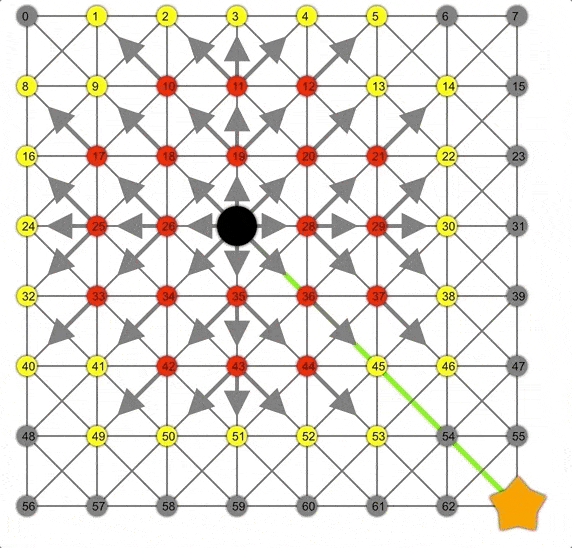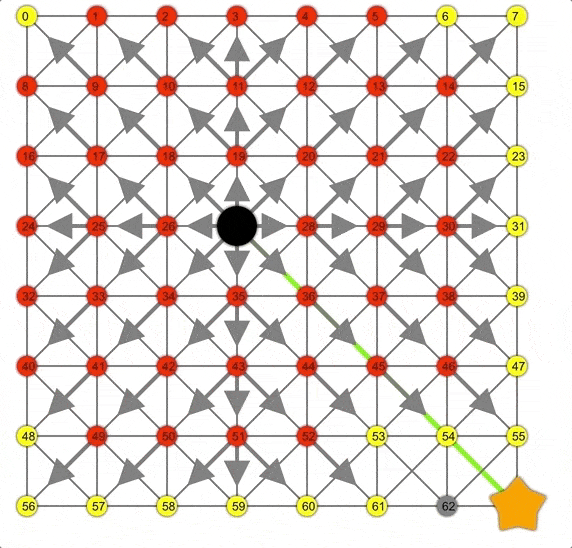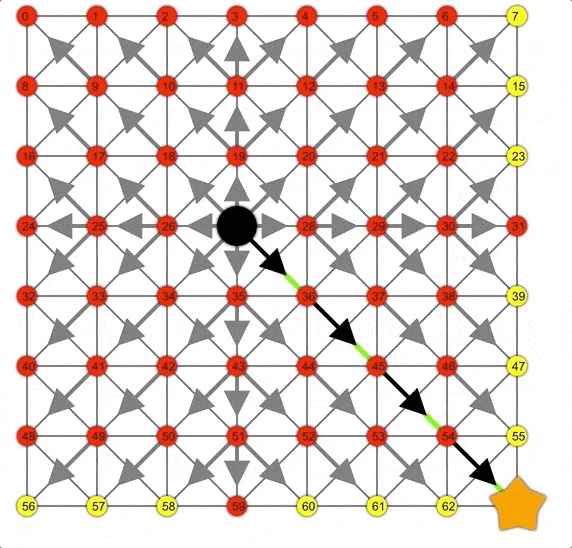
Dijkstra展示動(dòng)畫，注意此時(shí)的邊界是一個(gè)圓。

A*

為實(shí)現(xiàn)A*算法，需要傳遞一個(gè)實(shí)際啟發(fā)式函數(shù)，例如兩個(gè)節(jié)點(diǎn)之間的歐式距離。通過“節(jié)點(diǎn)成本”+“節(jié)點(diǎn)到目標(biāo)節(jié)點(diǎn)的估算成本”對節(jié)點(diǎn)進(jìn)行加權(quán)，通過優(yōu)先搜索更大可能的節(jié)點(diǎn)加快搜索速度。

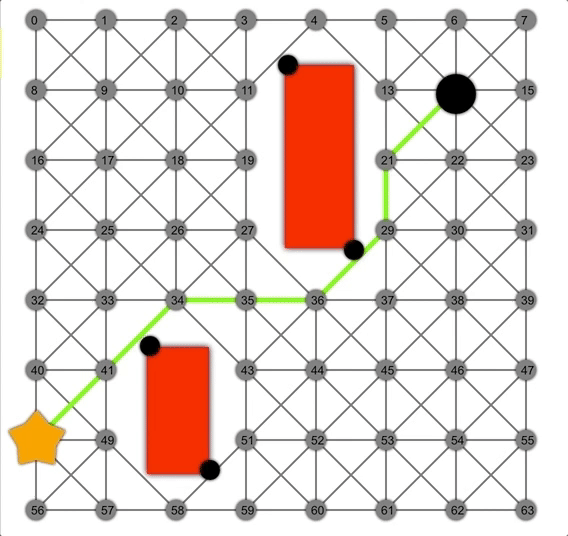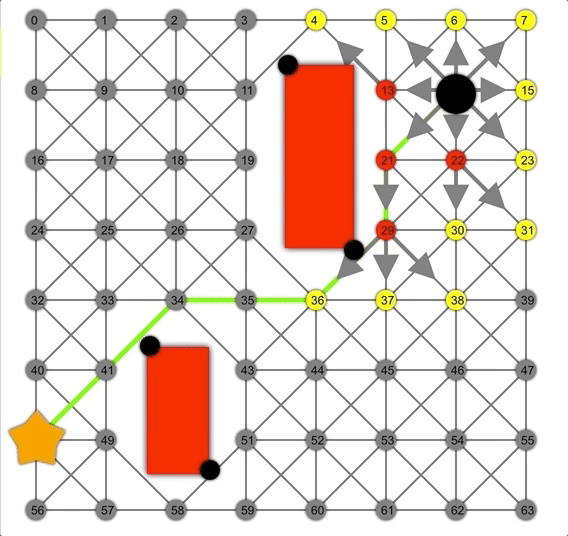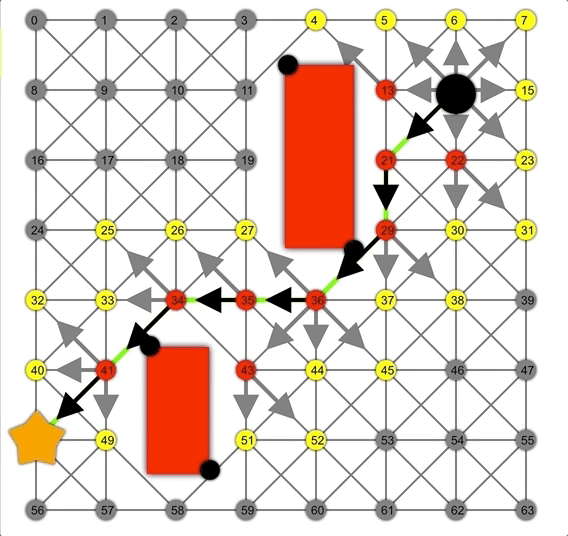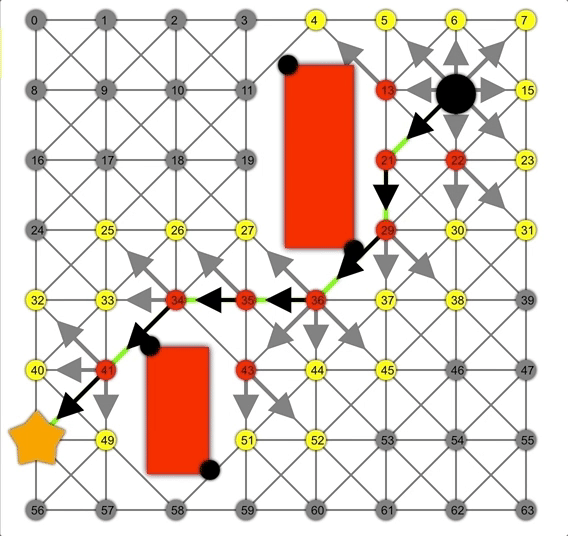
借助啟發(fā)式方法，A*可以比Dijkstra或BFS更快地找到正確路徑。

非允許的啟發(fā)式函數(shù)

只有應(yīng)用可允許啟發(fā)式函數(shù)，A*才能找到最短路徑，這也意味著算法永遠(yuǎn)不會(huì)高估實(shí)際路徑長度。由于歐氏距離是兩點(diǎn)之間的最短距離/路徑，因此歐氏距離絕不會(huì)超出。

但如果將其乘以常數(shù)k>0會(huì)怎樣呢？這樣會(huì)高估距離，成為非允許的啟發(fā)式函數(shù)。

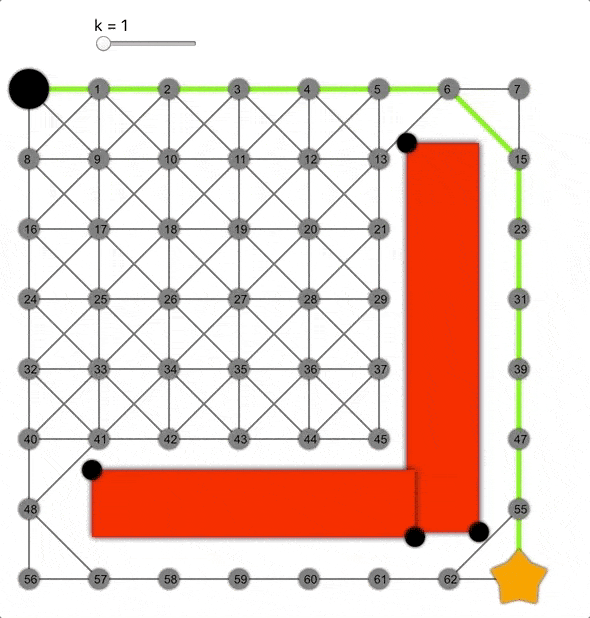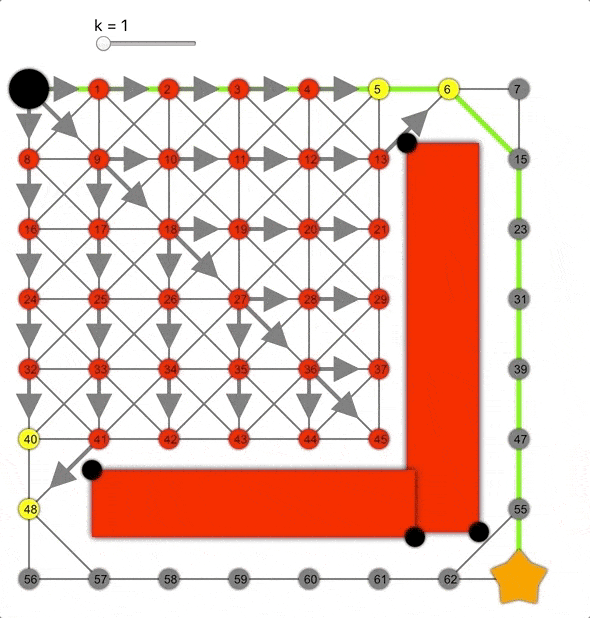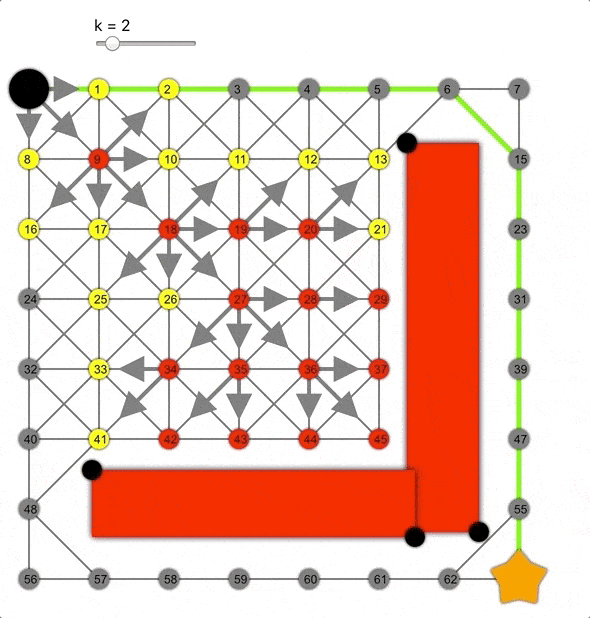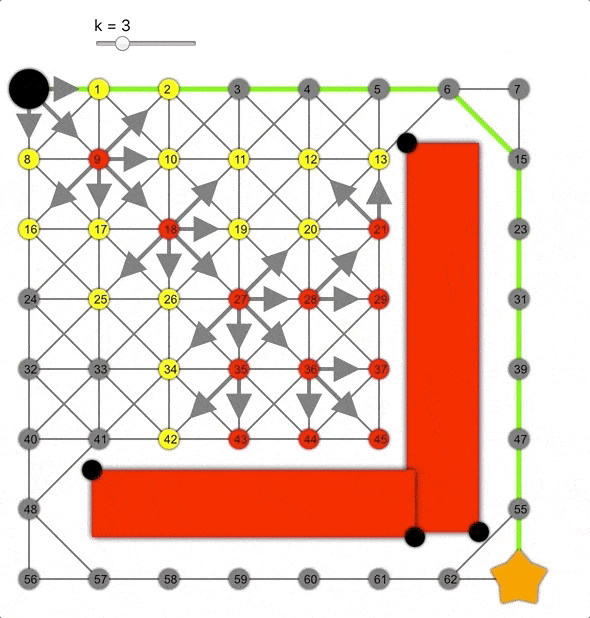
k值越大，算法越容易到達(dá)目標(biāo)，但同時(shí)準(zhǔn)確性降低，導(dǎo)致生成的路徑并非總是最短的。

算法實(shí)現(xiàn)

本項(xiàng)目通過Javascript實(shí)現(xiàn)，以便讀者在Web上進(jìn)行訪問。另外，我使用react渲染UI，使用react-konva渲染圖形。

路徑發(fā)現(xiàn)是指接受隊(duì)列類型和啟發(fā)式函數(shù)，并返回另一個(gè)函數(shù)，即真實(shí)路徑發(fā)現(xiàn)（稱為currying）。

這樣，用戶每次更改設(shè)置后，都會(huì)使用確定參數(shù)創(chuàng)建一個(gè)新的路徑發(fā)現(xiàn)函數(shù)，并將之用于圖搜索。

為可視化路徑發(fā)現(xiàn)的步驟，我使用javascript生成器，這意味著函數(shù)返回一個(gè)迭代器，而不僅僅是一個(gè)值。因此，訪客在每一步都可以生成算法的整個(gè)狀態(tài)，并將其保存到數(shù)組，然后通過頁面頂部的滑塊顯示特定狀態(tài)。

此鏈接進(jìn)入交互演示頁面：https://interactive-pathfinding.netlify.com/