[[361000]]

本文轉(zhuǎn)載自微信公眾號(hào)「 不正經(jīng)的前端」，作者 不正經(jīng)的前端。轉(zhuǎn)載本文請(qǐng)聯(lián)系 不正經(jīng)的前端公眾號(hào)。

寫(xiě)在前面

可能有些人會(huì)吐槽，學(xué)算法有什么用，頂多就是去面試大廠的時(shí)候能用上，大廠面試算法也只是強(qiáng)中篩強(qiáng)的一個(gè)敲門(mén)磚而已，我又不去面大廠，不用學(xué)它，真的是這樣嗎?

肯定不是，在計(jì)算機(jī)行業(yè)發(fā)展，不管是前端亦或是后端，算法都是進(jìn)階的一個(gè)絆腳石，可以說(shuō)不會(huì)算法永遠(yuǎn)也成不了一個(gè)合格的高級(jí)工程師，想要進(jìn)大廠確實(shí)要會(huì)些算法，但是它并不只是為了面試，它和我們的程序是息息相關(guān)的，有人說(shuō)前端不需要算法?你把大名鼎鼎的 虛擬DOM (Virtual DOM) 置于何地，它就是 算法與數(shù)據(jù)結(jié)構(gòu) 的一種體現(xiàn)，可能又有人會(huì)說(shuō)了，我又不寫(xiě)虛擬DOM。。。嗯，那你總想要賺錢(qián)吧，走技術(shù)路線想拿高薪，算法是基石

網(wǎng)上有很多算法文章以及課程，說(shuō) 7 天學(xué)會(huì)算法數(shù)據(jù)結(jié)構(gòu)，30 天掌握算法與數(shù)據(jù)結(jié)構(gòu)等等等等，別傻了，算法沒(méi)有捷徑，只能靠我們一點(diǎn)一點(diǎn)累積，你要做的首先就是相信自己不是天才，其次是每天堅(jiān)持刷題，時(shí)間緊可以一周刷四五題，最好速度是每天一題，后期時(shí)間充裕或者熟練了甚至可以一天刷幾題，即使很聰明的人在一段時(shí)間不接觸算法后，還是會(huì)忘掉，所以重要的是持續(xù)下去

接下來(lái)我們來(lái)從零開(kāi)始學(xué)習(xí)算法吧，如果你未曾刷過(guò)算法，這篇文章會(huì)帶你了解什么是算法，什么是數(shù)據(jù)結(jié)構(gòu)，在刷算法的同時(shí)，我們要明確自己的解法是否足夠優(yōu)質(zhì)，而判斷優(yōu)質(zhì)解發(fā)會(huì)通過(guò)時(shí)間以及空間兩個(gè)維度來(lái)體現(xiàn)，本文更會(huì)重點(diǎn)介紹，這些都是刷算法之前需要必備的知識(shí)，如果能為你的算法之路帶來(lái)啟蒙，那真是太棒了，十分榮幸，如果你已經(jīng)了解了這些知識(shí)，那么不妨快速閱讀下，看看是否能為你的算法知識(shí)做些擴(kuò)充，當(dāng)然如果有錯(cuò)誤的地方，你也可以為我指引，更是十分榮幸

什么是數(shù)據(jù)結(jié)構(gòu)

數(shù)據(jù)結(jié)構(gòu)其實(shí)就是是程序存儲(chǔ)組織數(shù)據(jù)的方式，一個(gè)數(shù)據(jù)結(jié)構(gòu)是由程序中的數(shù)據(jù)元素按照某種邏輯關(guān)系組織起來(lái)的，是若干個(gè)數(shù)據(jù)元素的組合

數(shù)據(jù)結(jié)構(gòu)是程序中處理數(shù)據(jù)的基本單位，在程序中作為一個(gè)整體來(lái)使用

例如一個(gè)數(shù)字 1 或者一個(gè)字符 A，它是一種數(shù)據(jù)結(jié)構(gòu)

例如一個(gè)日期 2020年12月14日，它由年月日這 3 種格式組成，也是一種數(shù)據(jù)結(jié)構(gòu)

例如一個(gè)數(shù)組 [1, 'a', '2020年12月14日']，它是由數(shù)字、字符、日期格式組合而成，也是一種數(shù)據(jù)結(jié)構(gòu)

通俗來(lái)說(shuō)，用一定格式組成的數(shù)據(jù)都是數(shù)據(jù)結(jié)構(gòu)，我們比較常見(jiàn)的數(shù)據(jù)結(jié)構(gòu)有字符串、數(shù)組、對(duì)象、堆、棧、鏈表、樹(shù)、哈希表等等，你可能對(duì)著其中的一些數(shù)據(jù)結(jié)構(gòu)并不了解，不要擔(dān)心，你并不需要立刻知道它們都是什么，對(duì)于前端來(lái)說(shuō)，我們使用 JavaScript 這個(gè)令我們又愛(ài)又恨的語(yǔ)言，它本身就存在的數(shù)據(jù)結(jié)構(gòu)很少，那么對(duì)于像鏈表、樹(shù)等等這些結(jié)構(gòu)都是通過(guò)對(duì)象來(lái)模擬的，這點(diǎn)要先知道

在許多程序設(shè)計(jì)當(dāng)中，數(shù)據(jù)結(jié)構(gòu)的選擇是一個(gè)基本的設(shè)計(jì)考慮因素，系統(tǒng)實(shí)現(xiàn)的困難程度和系統(tǒng)構(gòu)造的質(zhì)量都嚴(yán)重依賴于是否選擇了最優(yōu)的數(shù)據(jù)結(jié)構(gòu)，選擇最優(yōu)的數(shù)據(jù)結(jié)構(gòu)能夠有效的提高運(yùn)行的效率和節(jié)約存儲(chǔ)空間的使用，但是要知道，沒(méi)有十全十美的數(shù)據(jù)結(jié)構(gòu)，每種數(shù)據(jù)結(jié)構(gòu)都有局限性同樣也有優(yōu)點(diǎn)，要根據(jù)需求來(lái)選擇合適的數(shù)據(jù)結(jié)構(gòu)

什么是算法

什么是算法，我們都知道 1+2+3=6，為什么等于 6 呢，你可能會(huì)說(shuō)，1 加 2等于 3，兩個(gè) 3 相加等于 6，這是小學(xué)生都會(huì)的數(shù)學(xué)常識(shí)，它就是廣義上的算法

算法其實(shí)就是解決一個(gè)問(wèn)題的完整步驟描述，是指完成一個(gè)任務(wù)準(zhǔn)確而完整的步驟描述

算法的設(shè)計(jì)很多時(shí)候需要取決于數(shù)據(jù)結(jié)構(gòu)，而算法的實(shí)現(xiàn)更依賴于采用的數(shù)據(jù)結(jié)構(gòu)

提出一個(gè)問(wèn)題的算法是一個(gè)從抽象到具體的過(guò)程

• 分析問(wèn)題，選擇數(shù)據(jù)結(jié)構(gòu)，得出初步的解決方法
• 將解決方法合理地拆分，整理成許多步驟
• 為重復(fù)的步驟選擇合理的循環(huán)變量
• 使用易轉(zhuǎn)化為程序?qū)崿F(xiàn)的自然語(yǔ)言簡(jiǎn)練地描述算法

了解了什么是算法之后，我們來(lái)看時(shí)間和空間復(fù)雜度，衡量不同算法之間的優(yōu)劣我們通常從兩個(gè)維度來(lái)考究

• 時(shí)間維度：指執(zhí)行代碼所消耗的時(shí)間，即時(shí)間復(fù)雜度
• 空間維度：指執(zhí)行代碼所消耗的空間，即空間復(fù)雜度

接下來(lái)就開(kāi)始逐步剖析時(shí)間和空間復(fù)雜度了，先說(shuō)時(shí)間復(fù)雜度

時(shí)間復(fù)雜度

在說(shuō)時(shí)間復(fù)雜度之前，我們首先要理解一個(gè)概念即代碼執(zhí)行次數(shù)，也可稱之為語(yǔ)句頻度或時(shí)間頻度，用 T(n) 表示

我們用例子來(lái)一步一步闡述，首先我們來(lái)看函數(shù) fn1

function fn1(){ 
  console.log("句末") 
  console.log("isboyjc") 
} 

我們來(lái)看這個(gè)函數(shù)中的語(yǔ)句會(huì)執(zhí)行多少次

很明顯此函數(shù)內(nèi)部只有兩個(gè)語(yǔ)句，即 console.log("句末") 和 console.log("isboyjc")，那么我們說(shuō)這個(gè)函數(shù)體內(nèi)代碼執(zhí)行次數(shù)是 2

我們?cè)賮?lái)看函數(shù) fn2

function fn2(n){ 
  for(let i = 0; i < n; i++){ 
    console.log("句末") 
  } 
} 

我們先來(lái)看函數(shù) fn2 中有幾條可執(zhí)行語(yǔ)句

let i = 0 
i < n 
i++ 
console.log("句末") 

我們假設(shè) n = 3，然后依次帶入進(jìn)去，看看各個(gè)執(zhí)行語(yǔ)句執(zhí)行了多少次

let i = 0 此條聲明語(yǔ)句只在第一次 for 循環(huán)聲明時(shí)執(zhí)行 1 次

i < n 此條語(yǔ)句執(zhí)行次數(shù)根據(jù)形參 n 的大小變化，n = 3 時(shí)，即 i=0,i=1,i=2,i=3 時(shí)會(huì)執(zhí)行，即此條語(yǔ)句執(zhí)行次數(shù)為 n + 1 次

i++ 此條語(yǔ)句執(zhí)行次數(shù)也是根據(jù)形參 n 的大小變化，n = 3 時(shí)，即 i=0,i=1,i=2 時(shí)會(huì)執(zhí)行，即 n 次

console.log("句末") 此條語(yǔ)句執(zhí)行次數(shù)還是根據(jù)形參 n 的大小變化，n = 3 會(huì)執(zhí)行 3 次，那么此語(yǔ)句在函數(shù)內(nèi)部即會(huì)執(zhí)行 n 次

1 + (n + 1) + n + n = (3n + 2) 

那么函數(shù) fn2 內(nèi)共執(zhí)行 3n + 2 次

一段代碼的總執(zhí)行次數(shù)我們通常會(huì)用 T(n) 來(lái)表示，那么調(diào)用一次上面 fn1/fn2 兩函數(shù)的總執(zhí)行次數(shù)即

T(n) = 2   // fn1 
T(n) = 3n + 2 // fn2 

上面的 n，指的是為問(wèn)題的規(guī)模，即輸入數(shù)據(jù)的大小或者說(shuō)數(shù)量，你也可以簡(jiǎn)單的理解為 T 就是函數(shù)本身，n 就是參數(shù)，也就是說(shuō)

函數(shù) fn1 任何情況下執(zhí)行次數(shù)都為 2

函數(shù) fn2 的總執(zhí)行次數(shù)會(huì)根據(jù) n 的大小變化而產(chǎn)生一個(gè)變化

我們思考一下，我們可以使用一段代碼的執(zhí)行總次數(shù)來(lái)衡量執(zhí)行速度嗎?

答案當(dāng)然是不行的，當(dāng)代碼行數(shù)比較多的時(shí)候，我們一條一條的數(shù)來(lái)計(jì)算執(zhí)行總次數(shù)太麻煩了，例如函數(shù)中套用函數(shù)時(shí)、循環(huán)中套用循環(huán)時(shí)，想要精確計(jì)算執(zhí)行次數(shù)都是非常麻煩的

所以，在算法中，我們一般用 T(n) 簡(jiǎn)化后的估算值來(lái)表達(dá)代碼執(zhí)行的速度，通常我們用大些字母 O 來(lái)表示，即大 O 表示法，由于是估算，它表示的是代碼執(zhí)行時(shí)間隨數(shù)據(jù)規(guī)模增長(zhǎng)的變化趨勢(shì)，所以，也叫作漸進(jìn)時(shí)間復(fù)雜度(asymptotic time complexity)，簡(jiǎn)稱時(shí)間復(fù)雜度

明確了這個(gè)概念以后，我們就可以來(lái)算時(shí)間復(fù)雜度了，還是用上面 fn1/fn2 兩函數(shù)例

// fn1 
T(n) = 2 
 
// fn2 
T(n) = 3n + 2 

首先我們來(lái)看函數(shù) fn1，它的執(zhí)行總次數(shù)為 2，一個(gè) 常數(shù)(常數(shù)級(jí))，也就是說(shuō)此函數(shù)無(wú)論何時(shí)它的總執(zhí)行次數(shù)都是 2，是一個(gè)不變的值，那么我們使用時(shí)間復(fù)雜度 O 來(lái)表示時(shí)直接估算為 1 就可以，即時(shí)間復(fù)雜度為 O(1)

我們?cè)賮?lái)看函數(shù) fn2 ，它的執(zhí)行次數(shù) T(n) 是 3n + 2 即 常數(shù)*n + 常數(shù)，這里我們完全可以看成 常數(shù)*n 和 +常數(shù) 兩部分，隨著 n 的增大，只有前一個(gè)部分會(huì)有變化，后面是不變的，所以在表示時(shí)間復(fù)雜度時(shí)就可以忽略后面不變的常數(shù)，即 常數(shù)*n，而 常數(shù)*n 中過(guò)的常數(shù)我們也可以直接當(dāng)做 1，或者說(shuō)忽略掉這個(gè)作為系數(shù)的常數(shù)，那么最終可以得出函數(shù) fn2 的時(shí)間復(fù)雜度為 n，即 O(n)

「PS：曉得可能有人把數(shù)學(xué)知識(shí)還給老師了，所以解釋下」

「常數(shù)：」 常數(shù)就是指平常的數(shù)值，可簡(jiǎn)單的理解為固定不變的數(shù)值

**系數(shù)：**系數(shù)指代數(shù)式的單項(xiàng)式中的數(shù)字因數(shù)，例如 a = 1 * a ，則它的系數(shù)為 1，2b = 2 * b ，則它的系數(shù)為 2

我們?cè)賮?lái)舉個(gè)例子，如下面這個(gè)多項(xiàng)式代指一個(gè)函數(shù)的 T(n)，求它的時(shí)間復(fù)雜度

T(n) = 10n^4 + 100n^2 + 1000 

其實(shí)，對(duì)于多項(xiàng)式，我們只需要保留最高次項(xiàng)就行了，也就說(shuō)，保留 n 的最高次方數(shù)就可以了，這個(gè)例子中保留的也就是 n 的 4 次方，系數(shù)和常數(shù)皆可以忽略，最終得到的時(shí)間復(fù)雜度即為 O(n^4)

「結(jié)論：」

T(n) 為常數(shù)時(shí)，時(shí)間復(fù)雜度為 O(1) ，反之時(shí)間復(fù)雜度為 O(保留T(n)的最高次項(xiàng)并去掉最高次項(xiàng)的系數(shù))

接下來(lái)，我們看幾個(gè)例子來(lái)判斷下幾段代碼的時(shí)間復(fù)雜度

「例1：」

function fn01(){ 
  console.log("你看這是啥") 
  console.log("這是一個(gè)輸出") 
  console.log("哈哈哈") 
  let a = 1 
  return a 
} 

上面這個(gè)函數(shù) fn01 中只有一條條的語(yǔ)句，共執(zhí)行 5 次，毫無(wú)變化，時(shí)間復(fù)雜度即 O(1) ，此為常數(shù)級(jí)時(shí)間復(fù)雜度

「例2：」

function fn02(n){ 
  for(let i = 0; i < n; i++){ 
    console.log("這是一個(gè)輸出🎓") 
  } 
} 

如上，函數(shù) fn02 同上文中的例子 fn2，一個(gè)循環(huán)，時(shí)間復(fù)雜度即為 O(n) ，此為線性級(jí)時(shí)間復(fù)雜度

「例3：」

function fn03(n){ 
  for(let i = 0; i < n; i++){ 
    console.log("外層循環(huán)") 
    for(let j = 0; j < n; j++){ 
      console.log("內(nèi)層循環(huán)") 
    } 
  } 
} 

這個(gè)題和上面就不太一樣了，我們先單獨(dú)看內(nèi)部的循環(huán)，內(nèi)部循環(huán)大概會(huì)執(zhí)行 n 次，再來(lái)看外部循環(huán)又會(huì)執(zhí)行 n 次，最終也就是 n * n = n^2，即函數(shù) fn03 的時(shí)間復(fù)雜度為 O(n^2) ，此為平方級(jí)時(shí)間復(fù)雜度，如果是三層循環(huán)也就是時(shí)間復(fù)雜度為 O(n^3) 時(shí)，即立方級(jí)時(shí)間復(fù)雜度

從這里我們就可以看出來(lái)，一段代碼有多少層循環(huán)，時(shí)間復(fù)雜度就是 n 的多少次方，所以盡量避免多層循環(huán)嵌套

「例4：」

我們?cè)賮?lái)看下面這個(gè)函數(shù) fn04

function fn04(n){ 
  for(let i = 0; i < n; i++){ 
    console.log("外層循環(huán)") 
    for(let j = 0; j < n; j++){ 
      console.log("內(nèi)層循環(huán)") 
    } 
  } 
   
  for(let i = 0; i < n; i++){ 
    console.log("哈哈哈") 
  } 
} 

此函數(shù)中有一個(gè)雙循環(huán)，有一個(gè)單循環(huán)，即執(zhí)行次數(shù)大概是 n^2 + n，根據(jù)我們上面說(shuō)的保留最高次項(xiàng)，那么函數(shù) fn04 的時(shí)間復(fù)雜度即為 O(n^2)

「例5：」

算法中肯定不只是上面那種尋常的循環(huán)，再來(lái)看下面這一個(gè)

function fn05(n){ 
  for(let i = 0; i < n; i++){ 
    console.log("外層循環(huán)") 
    for(let j = i; j < n; j++){ 
      console.log("內(nèi)層循環(huán)") 
    } 
  } 
} 

其實(shí)遇到這種，我們直接帶入進(jìn)去試一試即可知其規(guī)律

當(dāng) i = 0 時(shí)，里層循環(huán)會(huì)執(zhí)行 n 次

當(dāng) i = 1 時(shí)，里層循環(huán)會(huì)執(zhí)行 n - 1 次

當(dāng) i = 2 時(shí)，里層循環(huán)會(huì)執(zhí)行 n - 2 次

當(dāng) i = 3 時(shí)，里層循環(huán)會(huì)執(zhí)行 n - 3 次

這個(gè)時(shí)候我們就發(fā)現(xiàn)了規(guī)律，每當(dāng) i 增加 1，里層循環(huán)就少執(zhí)行 1 次，那么就簡(jiǎn)單了

當(dāng) i = n - 2 時(shí)，里層循環(huán)會(huì)執(zhí)行 2 次

當(dāng) i = n - 1 時(shí)，里層循環(huán)會(huì)執(zhí)行 1 次

最終我們把 n 個(gè)里層循環(huán)的執(zhí)行次數(shù)相加即可得出最終的一個(gè)不精確的總執(zhí)行次數(shù)

T(n) = n + (n - 1) + (n - 2) + ... + 3 + 2 + 1 

如上，這是一個(gè)等差數(shù)列，嗯，曉得，會(huì)補(bǔ)充

如果一個(gè)數(shù)列從第二項(xiàng)起，每一項(xiàng)與它的前一項(xiàng)的差等于同一個(gè)常數(shù)，這個(gè)數(shù)列就叫做等差數(shù)列，而這個(gè)常數(shù)叫做等差數(shù)列的公差，公差常用字母 d 表示

例如：1,3,5,7,9……(2n-1) ，等差數(shù)列 S(n) 的通項(xiàng)公式為：S(n) = S1 + (n-1) * d，前 n 項(xiàng)和公式如下

S(n) = n*S1 + n*(n - 1)*d/2 
 
// 或 
 
S(n) = n*(S1 + Sn)/2 

如此我們計(jì)算結(jié)果就成，我們上面的數(shù)列中，公差 d 為 -1，帶入公式即可，第二個(gè)公式簡(jiǎn)單，用第二個(gè)好了，計(jì)算結(jié)果都是一樣的

// n*(S1 + Sn)/2 
 
n*(n + 1)/2 = (n^2 + n)/2 = (1/2)n^2 + (1/2)n 

最終我們得到了 (1/2)n^2 + (1/2)n ，按照上文中取最高次項(xiàng)去掉系數(shù)，即時(shí)間復(fù)雜度為 O(n^2)

「例6：」

再來(lái)看一個(gè)例子

function fn06(n){ 
  for(let i = 1; i < n; i *= 2){ 
    console.log("isboyjc") 
  } 
} 

還是老樣子，如果你不曉得怎么看，可以先帶入幾個(gè)參數(shù)試一下，看一看規(guī)律

我們可以分別使用 n=2, n=4, n=8, n=16，觀察其循環(huán)中打印次數(shù)，當(dāng)然你也可以直接運(yùn)行一下代碼，過(guò)程不過(guò)多闡述了，我們直接看結(jié)果

n=2  時(shí)打印1次 T(n)=1 
n=4  時(shí)打印2次 T(n)=2 
n=8  時(shí)打印3次 T(n)=3 
n=16  時(shí)打印4次 T(n)=4 

對(duì)于執(zhí)行次數(shù)產(chǎn)生主要影像的就是循環(huán)語(yǔ)句中的 i*=2，每次循環(huán) i 都會(huì)變成自身的兩倍，仔細(xì)觀察我們就可以得出這樣一個(gè)規(guī)律性結(jié)果

n=2  時(shí)打印1次 T(n)=1 // 2^1 = 2 
n=4  時(shí)打印2次 T(n)=2 // 2^2 = 4 
n=8  時(shí)打印3次 T(n)=3 // 2^3 = 8 
n=16  時(shí)打印4次 T(n)=4 // 2^4 = 16 

根據(jù)上面的規(guī)律我們不難發(fā)現(xiàn)，那么2^執(zhí)行次數(shù)=n，即 2^T(n)=n ，我們求 T(n)，調(diào)個(gè)就行了，也就是以 2 為底 n 的對(duì)數(shù)，即 T(n)=log_2 n

「PS：又來(lái)補(bǔ)數(shù)學(xué)了」

「對(duì)數(shù)：」 假如 a^n=b，即 a 的 n 次方等于 b，我們求 n 的值，那么這里為了方便表示就可以寫(xiě)成 log_a b，即以 a 為底 b 的對(duì)數(shù)，a 是底數(shù)，b 是真數(shù)，而 n 就是對(duì)數(shù)

你可能會(huì)在糾結(jié)為什么只觀察循環(huán)中的打印次數(shù)而不計(jì)算其所有的執(zhí)行次數(shù)，原因上面也說(shuō)過(guò)了，這些固有的常數(shù)及系數(shù)完全可以忽略，好吧，我們?cè)僮詈笸埔槐?/p>

中間輸出為 log_2 n 次，let i = 1 只會(huì)執(zhí)行一次，i

「例7：」

最后在給大家來(lái)一個(gè)例子吧

function fn07(n,m){ 
  for(let i = 0; i < n; i++){ 
    while(j < m){ 
      console.log("你看懂了嗎") 
      j = j * 2 
    } 
  } 
} 

如上圖，此函數(shù)有兩個(gè)參數(shù)，對(duì)應(yīng)了里外兩個(gè)循環(huán)，我們先從內(nèi)部循環(huán)看起，眼熟嗎?其實(shí)內(nèi)部循環(huán)和上題函數(shù) fn06 中的循環(huán)是一樣的，只是一個(gè)用的 for ，一個(gè)用的 while，上題中的時(shí)間復(fù)雜度我們就不再敘述了，那么內(nèi)層循環(huán)時(shí)間復(fù)雜度為 O(log n)

我們?cè)賮?lái)看外層循環(huán)，也是上面解釋過(guò)的，單看外層循環(huán)時(shí)間復(fù)雜度是 O(n)

兩個(gè)循環(huán)是嵌套關(guān)系，相乘就可以了，所以函數(shù) fn07 的時(shí)間復(fù)雜度即為 O(n*log n) ，也就是線性對(duì)數(shù)級(jí)時(shí)間復(fù)雜度

正如此函數(shù)輸出，你看懂了嗎?

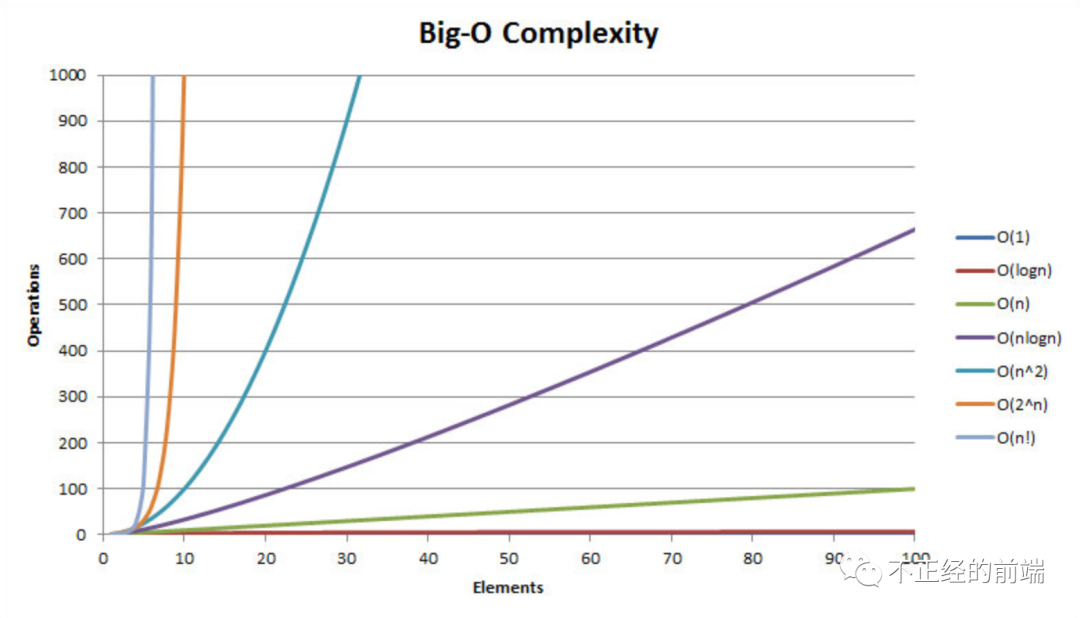
「碼字太累，看個(gè)圖吧：」

找了一張網(wǎng)圖(侵刪)，使用圖表來(lái)更加清晰的展示了常見(jiàn)的時(shí)間復(fù)雜度曲線

如上圖，橫坐標(biāo)為 n ，可以看到，不同時(shí)間復(fù)雜度隨著 n 的增大操作次數(shù)或者說(shuō)執(zhí)行時(shí)間的遞增趨勢(shì)

常見(jiàn)的時(shí)間復(fù)雜度量級(jí)有

• 常數(shù)級(jí) O(1)
• 對(duì)數(shù)級(jí) O(log n)
• 線性級(jí) O(n)
• 線性對(duì)數(shù)級(jí) O(n*log n)
• 平方級(jí) O(n^2)
• 立方級(jí) O(n^3)
• K次方級(jí) O(n^k)
• 指數(shù)級(jí) O(2^n)

上面從上到下依次時(shí)間復(fù)雜度越來(lái)越大，執(zhí)行效率越來(lái)越低，大部分常用的在上面的圖表中都有展示

所以在程序或是刷題中，我們應(yīng)該盡量使用低時(shí)間復(fù)雜度的方法

時(shí)間復(fù)雜度就到此為止了，我們也列舉了常見(jiàn)的時(shí)間復(fù)雜度，接下來(lái)我們來(lái)看看空間復(fù)雜度

空間復(fù)雜度

空間復(fù)雜度其實(shí)就是對(duì)一個(gè)算法或者說(shuō)一段代碼在運(yùn)行過(guò)程中占用存儲(chǔ)空間大小表達(dá)方式

我們上面講過(guò)了時(shí)間復(fù)雜度，那么再來(lái)說(shuō)空間復(fù)雜度會(huì)簡(jiǎn)單的很多

空間復(fù)雜度也就是 S(n) ，它同樣會(huì)用大O表示法來(lái)表示，我們直接上例子

「例1：」

function fn001(n){ 
  for(let i = 0; i < n; i++){ 
    console.log("空間復(fù)雜度") 
  } 
} 

首先，我們知道，空間復(fù)雜度和存儲(chǔ)空間有關(guān)，而存儲(chǔ)空間是由什么決定的，肯定是聲明的變量啊，我們直接來(lái)找函數(shù) fn001 中的變量聲明，只有一個(gè) i ，也就是說(shuō)此函數(shù)只有開(kāi)辟了一塊空間供 i 使用，那么空間復(fù)雜度 S(n) 即為 O(1) ，你可能會(huì)說(shuō) i 不是一直在變嗎，是的它是在變，但是不管怎么變，它還是一個(gè)數(shù)字，占用空間大小都一致

空間復(fù)雜度和時(shí)間復(fù)雜度一樣，當(dāng)代碼里聲明的變量是一個(gè)常量，不會(huì)根據(jù)傳入值的變化而變化，那么也它的空間復(fù)雜度是 O(1)

「例2：」

function fn002(n){ 
  let arr = [] 
  while(n--){ 
    arr.push(n) 
  } 
} 

這個(gè)例子中我們聲明了一個(gè)數(shù)組，我們知道數(shù)組中是可以存各種類型的，在循環(huán)中，我們根據(jù) n 的大小向數(shù)組 arr 中 push 元素，所以，n 多大，數(shù)組就有多少元素，就占用了多少空間，所以空間復(fù)雜度S(n) = O(n)

「空間復(fù)雜度小結(jié)」

空間復(fù)雜度里，只列出了兩個(gè)例子，是因?yàn)橐话闱闆r下，我們用不到其他的，空間復(fù)雜度一般只會(huì)是 O(1)/O(n)/O(n^2)，其它的很少見(jiàn)，當(dāng)然也有，我們?cè)谥懒藭r(shí)間復(fù)雜度再分析空間復(fù)雜度也很好分析，就不過(guò)多贅述了

關(guān)于分析空間復(fù)雜度，其實(shí)我們直接從聲明的變量入手就可以，看函數(shù)體內(nèi)聲明的變量根據(jù)傳入值的變化而變化來(lái)分析

另外，這里我們沒(méi)有列舉遞歸情況，「請(qǐng)注意」，遞歸就是函數(shù)套函數(shù)，像俄羅斯套娃一樣的，這中間其實(shí)有一個(gè)問(wèn)題，我們知道，遞歸函數(shù)，每層遞歸里都會(huì)開(kāi)辟一個(gè)遞歸棧，每次遞歸產(chǎn)生的變量等空間消耗都會(huì)存在遞歸棧中，這也是一個(gè)空間，不管你有沒(méi)有聲明變量，只要遞歸了遞歸棧它都存在，也就是說(shuō)只要存在遞歸的情況，基本上最少的空間復(fù)雜度也是 O(n) 了，所以我們盡可能的在能使用迭代的情況下就不使用遞歸

時(shí)間 VS 空間

開(kāi)頭我們說(shuō)了，評(píng)價(jià)一個(gè)算法的效率我們主要是從它的時(shí)間和空間兩個(gè)維度看，但是，通常我們?cè)谒惴ㄖ校瑫r(shí)間和空間就是魚(yú)和熊掌的關(guān)系，這時(shí)候可能一道算法題有兩種解法，一種時(shí)間復(fù)雜度低，但空間復(fù)雜度稍高，另一種則反之

這個(gè)時(shí)候怎么辦呢?細(xì)品就知道了，在開(kāi)發(fā)中，我們一般都是時(shí)間優(yōu)于空間的，你想啊，一個(gè)程序，用戶不會(huì)關(guān)心的占用了多少內(nèi)存，但是他會(huì)關(guān)心你這個(gè)程序他在使用時(shí)的執(zhí)行速度，況且，空間也就是磁盤(pán)，現(xiàn)階段磁盤(pán)我們可以花錢(qián)擴(kuò)容，時(shí)間上就沒(méi)這么簡(jiǎn)單了，所以某些相對(duì)的情況下，空間換時(shí)間是可以令人接受的

雖說(shuō)空間換時(shí)間可行，但也不能一味的空間換時(shí)間，我們還是要盡可能降低兩個(gè)維度的復(fù)雜度，少數(shù)對(duì)立情況下，可空間換時(shí)間

我們?cè)谒⑺惴ǖ臅r(shí)候，不是刷完了就完事了，我們還要去分析我們的題解對(duì)應(yīng)的時(shí)間及空間復(fù)雜度，可以分析多種題解之間的復(fù)雜度，對(duì)比找出最優(yōu)解

在面試的時(shí)候，假如面試官給你一道算法題，當(dāng)你知道好幾種解法的時(shí)候，完全可以很裝B的問(wèn)一下，您喜歡時(shí)間至上還是空間至上呢，我都能解，奧利給，說(shuō)完他就會(huì)讓你都寫(xiě)了??

開(kāi)個(gè)玩笑哈，面試的時(shí)候盡量寫(xiě)出多種解法并給面試官解釋各種解法時(shí)間及空間復(fù)雜度的不同，怎么說(shuō)?就很棒

最后

此文介紹算法一些理論基礎(chǔ)，理解之后就可以刷題了，推薦按照數(shù)據(jù)結(jié)構(gòu)類型來(lái)每天刷一題，建議上班無(wú)聊時(shí)刷題，上班摸魚(yú)水群不如摸魚(yú)刷道算法，百利無(wú)一害，堅(jiān)持每天刷題吧，加油

GitHub建了個(gè)算法倉(cāng)庫(kù)，從零更算法題/文字/視頻 題解ing，一塊來(lái)刷吧 ?? GitHub傳送門(mén)[1]

準(zhǔn)備算法每篇每題都錄個(gè)視頻版，主要是為了跟思路講一遍手寫(xiě)下，講的可能不好，此文視頻詳見(jiàn) ?? B站傳送門(mén)[2]

看到這里了，來(lái)個(gè)三連吧，如有錯(cuò)誤請(qǐng)指正，也歡迎大家關(guān)注公眾號(hào)「不正經(jīng)的前端」，和算法群的朋友們組團(tuán)刷算法，效率更高

Reference

[1]GitHub傳送門(mén):

https://github.com/isboyjc/DailyAlgorithms

[2]B站傳送門(mén):

https://www.bilibili.com/video/BV1T5411p7oN