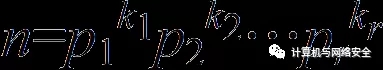[[357279]]

微信公眾號：計算機與網絡安全

ID：Computer-network

傳統的加密方法是加密、解密使用同樣的密鑰，由發送者和接收者分別保存，在加密和解密時使用。采用這種方法的主要問題是密鑰的生成、注入、存儲、管理、分發等很復雜，特別是隨著用戶數量的增加，密鑰的需求量成倍增加。在網絡通信中，大量密鑰的分配是一個難以解決的問題。

為了解決常規密鑰密碼體制的密鑰分配問題，滿足用戶對數字簽名的需求，1976年，美國學者Diffie和Hellman發表了著名論文《密碼學的新方向》，提出了建立“公開密鑰密碼體制”：若用戶A有加密密鑰ka(公開)，不同于解密密鑰ka′(保密)，要求ka的公開不影響ka′的安全;若用戶B要向用戶A保密傳送明文m，則可查用戶A的公開密鑰ka，若用ka加密得到密文c，則用戶A收到c后，用只有用戶A自己才掌握的解密密鑰ka′對c進行解密以得到m。

1978年，美國麻省理工學院的研究小組成員李維斯特(Rivest)、沙米爾(Shamir)和艾德曼(Adleman)(如圖1所示)提出了一種基于公鑰密碼體制的優秀加密算法——RSA算法。RSA算法是第一個比較完善的公開密鑰算法，它既能用于加密，也能用于數字簽名。RSA算法以它的三個發明者Rivest，Shamir，Adleman的名字首字母命名，這個算法經受住了多年深入的密碼分析。密碼分析者既不能證明也不能否定RSA算法的安全性，但這恰恰說明該算法有一定的可信性。目前，RSA算法已經成為最流行的公開密鑰算法。

 

 

 

[[357280]]

 

圖1 RSA公開密鑰算法的發明人

注：從左到右依次為李維斯特、沙米爾和艾德曼，照片拍攝于1978年

1、RSA算法原理

RSA是最著名且應用最廣泛的公開密鑰算法，可以同時用于加密和數字簽名。國際標準化組織(International Organization for Standardization，ISO)在1992年頒布的國際標準X.509中，將RSA算法正式納入國際標準。1999年，美國參議院通過立法，規定了數字簽名與手寫簽名的文件、郵件在美國具有同等的法律效力。

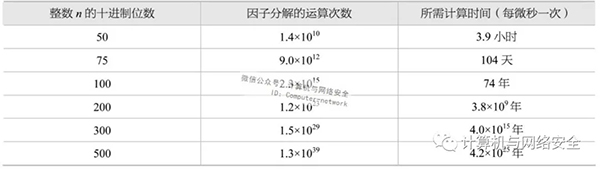
RSA算法是一種分組密碼體制算法，它的保密強度是建立在具有大素數因子的合數上的，其因子分解較困難。RSA算法的公鑰和私鑰選擇一對大素數(100到200位十進制數或更大的數)的函數。而從一個公鑰和密文恢復出明文的難度，等價于分解兩個大素數之積(這是公認的數學難題)，但是否為NP問題尚不確定。表1給出了大數分解難度的例子。

 

 

 

 

表1 大數分解難度舉例

RSA算法體制包括：一個公開密鑰KU={e，n}，一個私有密鑰KR={d，n}。其公鑰、私鑰的組成以及加密、解密的公式如表2所示。

 

 

 

 

表2 RSA算法

① 有可能找到e、d、n的值，使得對所有的M

② 對于所有的M

③ 在給定e和n時，計算出d是不可行的。

(1)RSA算法的數論基礎

下面介紹RSA算法中需要使用的幾個術語。

1)素數

素數又稱為質數，是指在大于1的自然數中，除了1和此數自身外，不能被其他自然數整除的數。例如，15=3×5，所以15不是素數;又如，12=6×2=4×3，所以12也不是素數。而13除了等于13×1以外，不能再表示為其他任何兩個整數的乘積，所以13是一個素數。

2)互為素數

公約數只有1的兩個自然數，叫作互質數，即互素數。兩個自然數是否互為素數的判別方法主要有以下8種(不限于此)。

① 兩個質數一定是互質數，例如，2與7，13與19。

② 一個質數如果不能整除另一個合數，那么這兩個數為互質數，例如，3與10，5與26。

③ 1不是質數也不是合數，它和任何一個自然數都是互質數，例如，1和9908。

④ 相鄰的兩個自然數是互質數，例如，15與16。

⑤ 相鄰的兩個奇數是互質數，例如，49與51。

⑥ 大數是質數的兩個數是互質數，例如，97與88。

⑦ 小數是質數，大數不是小數的倍數的兩個數是互質數，例如，7與16。

⑧ 兩個數都是合數(兩數之差又較大)，小數所有的質因數都不是大數的約數，這兩個數是互質數。例如，357與715，357=3×7×17，而3、7和17都不是715的約數，所以這兩個數為互質數。

3)模運算

模運算是整數運算，有一個整數m，以n為模做模運算，即mmod n。令m被n整除，只取所得的余數作為結果，就叫作模運算。例如，10 mod 3=1，26 mod 6=2，28 mod 2=0等。

模運算有以下性質。

① 同余性：若amod n=bmod n，則正整數a與b同余。

② 對稱性：若a=b mod n，則b=amod n。

③ 傳遞性：若a=b mod n，b=cmod n，則a=cmod n。

4)Euler函數

任意給定正整數n，計算在小于或等于n的正整數之中有多少個與n能構成互質關系的方法叫作歐拉函數，以φ(n)表示。例如，φ(8)=4，這是因為在1~8之中與8能形成互質關系的數有4個：1，3，5，7。

φ(n)的計算方法并不復雜，下面分情況對其進行討論。

第一種情況：如果n=1，則φ(1)=1，因為1與任何數(包括其自身)都能構成互質關系。

第二種情況：如果n是素數，則φ(n)=n-1，因為質數與每個小于它的數都能構成互質關系。

第三種情況：如果n是素數的某一個次方，如n=pk，p為素數，k≥1，則

φ(pk)=pk-pk-1

例如，φ(8)=φ(23)=23-22=4。這是因為只有當一個數不包含素數p時，才能與n互質。而包含素數p的數一共有pk-1個，即1×p、2×p、…、pk-1×p。

第四種情況：如果n可以分解成兩個互質的整數之積，例如，n=p1×p2，則φ(n)=φ(p1p2)=φ(p1)φ(p2)，即積的歐拉函數等于各個因子的歐拉函數之積。例如，φ(56)=φ(7×8)=φ(7)×φ(8)=6×4=24。

第五種情況：對于任意大于1的整數，若其可以寫成一系列素數的積，如

 

 

 

 

，則有

 

 

 

 

。

5)歐拉定理

如果兩個正整數a和n互質，則n的歐拉函數φ(n)滿足：

aφ(n)≡1(mod n)

即a的φ(n)次方減去1，被n整除。例如，3和7互質，φ(7)=6，(36-1)/7=104。

如果正整數a與質數p互質，則因為φ(p)=p-1，所以歐拉函數可寫成：

ap−1≡1(mod p)

這就是著名的費馬小定理(Fermat Theory)。

6)費馬小定理

若m是素數，且a不是m的倍數，則am-1 mod m=1。或者，若m是素數，則ammod m=a。例如，46mod 7=4096 mod 7=1，47mod 7=16384 mod 7=4。

推論：對于互素的a和n，有aφ(n)mod n=1。

(2)素數的產生與檢驗

首先來介紹素數的簡單判定算法。在C程序設計中，素數的判定算法為：給定一個正整數n，用2到sqrt(n)之間的所有整數去除n，如果可以整除，則n不是素數，如果不可以整除，則n是素數。這個算法的時間復雜度為O(sqrt(n))，算法描述簡單，實現也不困難。但是，這個算法對于位數較大的素數判定就顯得力不從心了。

目前，適用于RSA算法的最實用的素數產生辦法是概率測試法。該法的思想是隨機產生一個大奇數，然后測試其是否滿足條件，若滿足，則該大奇數可能是素數，否則，其是合數。

由于素數有無窮多個，因此判定一個整數是不是素數一直是一個大難題，威爾遜定理(Wilson's Theorem)就是其中的一種判定方法。

威爾遜定理：若正整數n>1，則n是一個素數當且僅當(n-1)! ≡ -1(mod n)。

雖然說威爾遜定理給出了素數的等價命題，但是由于階乘的增長速度太快(如13!為60多億)，因此其實際操作價值不高。由此提出了概率檢驗方法。

米勒-拉賓素性檢驗(Miller-Rabin Prime Test)是一種典型的概率檢驗方法。可以證明單次Miller-Rabin的正確概率大于3/4，我們重復若干次就可以增大這個概率。Miller-Rabin雖然有一定的概率出錯，但實踐證明，在重復20次的情況下，107以內的質數不會判斷出錯。

2、RSA加解密算法過程

(1)RSA加密算法過程

RSA加密算法的過程如下：

① 取兩個隨機大素數p和q(保密);

② 計算公開的模數n=p×q(公開);

③ 計算秘密的歐拉函數φ(n)=(p-1)×(q-1)(保密)，丟棄p和q，不要讓任何人知道;

④ 隨機選取整數e，使其滿足gcd(e,φ(n))=1(公開e加密密鑰);

⑤ 計算d，使其滿足de≡1(mod φ(n))(保密d解密密鑰);

⑥ 將明文X按模為r自乘e次冪以完成加密操作，從而產生密文Y(X、Y值在0到n-1范圍內)，即Y=Xemod n;

⑦ 解密，將密文Y按模為n自乘d次冪，得X=Ydmod n。

在RSA加(解)密算法實現過程中，主要的運算量是計算模的逆元以及模指數，通常情況下，計算模的逆元時會采用擴展的歐幾里德算法。

(2)RSA解密算法過程

由于指數較大，因此RSA解密過程比較耗時，但利用孫子定理(Chinese Remainder Theorem，CRT)可提高解密算法效率。CRT對RSA解密算法生成兩個解密方程(利用M=Cdmod pq)，即：M1=Mmod p=(Cmod p)d mod (p-1)mod p，M2=Mmod q=(Cmod q)d mod (q-1)mod q。

解方程M=M1mod p和M=M2mod q，可求得其具有唯一解。

3、RSA算法應用

(1)RSA用于數字簽名

① 簽名：對任意消息m∈M，用戶使用自己的私鑰簽名如下：S≡md(mod n)，進而可以得到簽名的消息(m, S)。

② 驗證簽名：由該用戶的公開密鑰(e, n)，驗證m≡Se(mod n)是否成立。

(2)RSA加密算法實例

可以通過一個簡單的例子來理解RSA的工作原理。為了便于計算，在以下實例中只選取小數值的素數p, q以及e，假設用戶A需要將明文“key”通過RSA加密后傳遞給用戶B，過程如下。

1)設計公私密鑰(e,n)和(d,n)

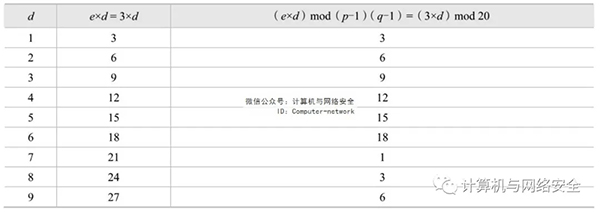
令p=3，q=11，得出n=p×q=3×11=33;f(n)=(p-1)(q-1)=2×10=20;取e=3(3與20互質)，則e×d≡1 mod f(n)，即3×d≡1 mod 20。d的取值可以用試算的辦法來確定。試算結果如表3所示。

 

 

 

 

表3 d的取值試算結果

通過試算得出，當d=7時，e×d≡1 mod f(n)同余等式成立。因此，可令d=7，從而可以設計出一對公私密鑰，加密密鑰(公鑰)為：KU=(e,n)=(3,33)，解密密鑰(私鑰)為：KR=(d,n)=(7,33)。

2)英文數字化

將明文信息數字化，并將其以每塊兩個數字進行分組。假定明文英文字母編碼表為按字母順序排列的數值，如表4所示。

 

 

 

 

表4 明文英文字母編碼表

則可得到分組后的key的明文信息為：11，05，25。

3)明文加密

用戶加密密鑰(3,33)將數字化明文分組信息加密成密文。由C≡Me(mod n)得：

C1=(M1)d(modn)=113(mod33)=11

C2=(M2)d(modn)=053(mod33)=26

C3=(M3)d(modn)=253(mod33)=16

因此，得到相應的密文信息為：11，26，16。

4)密文解密

用戶B收到密文后，若要將其解密，則只需要計算M≡Cd(mod n)，即：

M1=(C1)d(modn)=117(mod33)=11

M2=(C2)d(modn)=317(mod33)=05

M3=(C3)d(modn)=167(mod33)=25

用戶B得到的明文信息為：11，05，25。根據上面的編碼表將其轉換為英文，即可得到恢復后的原文“key”。

當然，實際運用要比這復雜得多。由于RSA算法的公鑰私鑰的長度(模長度)須達到1024位甚至2048位才能保證安全，因此，p、q、e的選取、公鑰私鑰的生成、加密解密模指數的運算都有一定的計算程序，需要依賴計算機的高速計算能力來完成。

4、RSA加解密算法的安全性

在RSA密碼應用中，公鑰KU是被公開的，即e和n的數值可以被第三方竊聽者得到。破解RSA密碼的關鍵在于從已知的e和n的數值(n等于pq)中求出d的數值，從而得到私鑰以破解密文。從上文中的公式：d≡e-1(mod((p-1)(q-1)))或de≡1(mod((p-1)(q-1)))可以看出，密碼破解的實質問題是：從pq這一數值求出(p-1)和(q-1)。換句話說，只要求出p和q的值，就能求出d的值進而得到私鑰。

若p和q是大素數，則從它們的積pq去分解因子p和q，就是一個公認的數學難題。例如，當pq大到1024位時，迄今為止還沒有人能夠利用任何計算工具完成其分解因子這一任務。因此，RSA從被提出到現在40余年，經歷了各種攻擊的考驗，逐漸為人們所接受，被普遍認為是目前最優秀的公鑰方案之一。

然而，雖然RSA的安全性依賴于大數的因子分解，但并沒有從理論上證明破譯RSA的難度與大數分解的難度等價，即RSA的重大缺陷是無法從理論上把握它的保密性能。

此外，RSA的缺點還有：

① 產生密鑰很麻煩，會受到素數產生技術的限制，因而難以做到一次一密;

② 分組長度太大，為保證安全性，n至少需要600 bits 以上，運算代價高，速度慢，較對稱密碼算法慢幾個數量級，且隨著大數分解技術的發展，這個長度還在增加，不利于數據格式的標準化。

因此，使用RSA只能加密少量數據，大量的數據加密還要依靠對稱密碼算法。