[[353954]]

本文轉載自微信公眾號「小明菜市場」，作者小明菜市場 。轉載本文請聯系小明菜市場公眾號。

Hello ! 我是小小，今天總結一下什么是樹，以及關于樹的一些內容。。

樹

樹是一種非常常用的數據結構，與線性表，堆棧并駕齊驅。

樹的定義

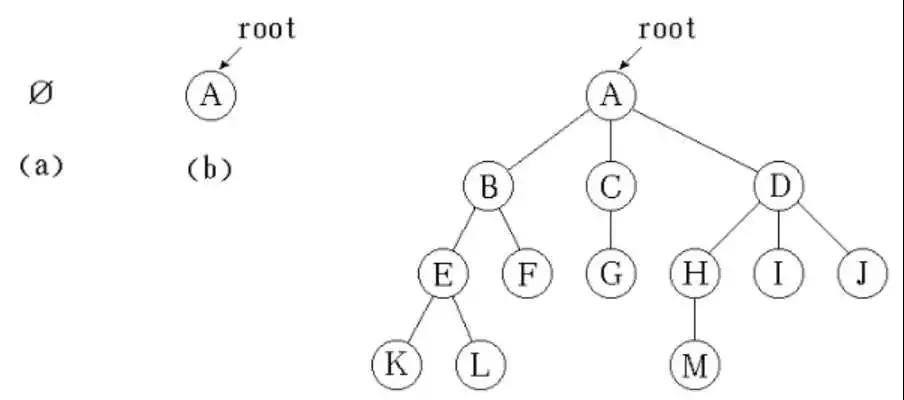
樹是從自然界抽象出來的，它指的是N個父子節點的有限集合，對于這個有限集合，需要滿足如下條件：

1. 當N=0時，該節點集合為空，這棵樹也為空
2. 在任意非空樹中，只能有一個根節點
3. 當N>1時，除去跟節點意外的其余節點本身也要集合成為一顆樹。即，樹具有遞歸特性，一棵樹是由若干子樹組成，每顆樹又是由若干顆更小的子樹組成，如圖所示

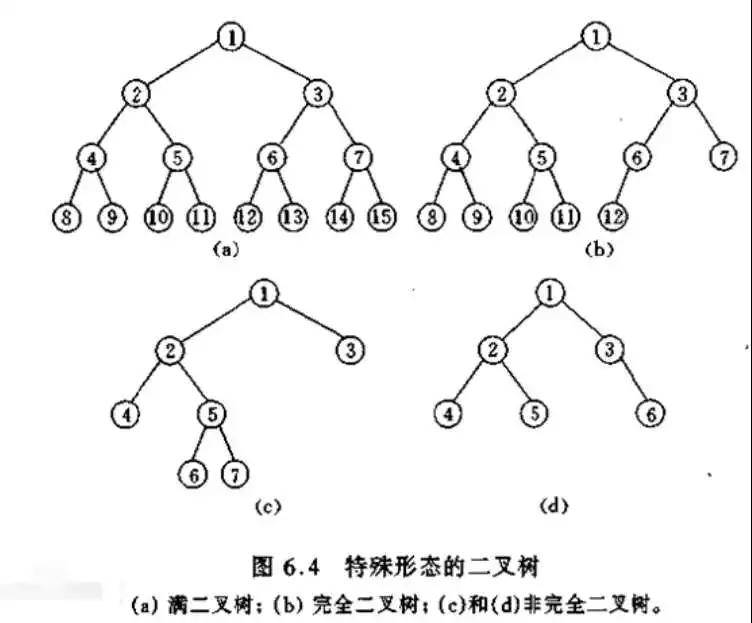
二叉樹

二叉樹指每個節點最多只能有兩個子樹的有序樹。通常左邊子樹稱之為左子樹，右邊樹稱之為右子樹。二叉樹最多只能有兩顆對稱的樹，二叉樹有左，右之分。樹和二叉樹的區別

1. 樹的節點的度數沒有限制，二叉樹限制為2，樹沒有限制。

2. 無序樹的節點沒有左右之分，二叉樹的節點有左右之分。

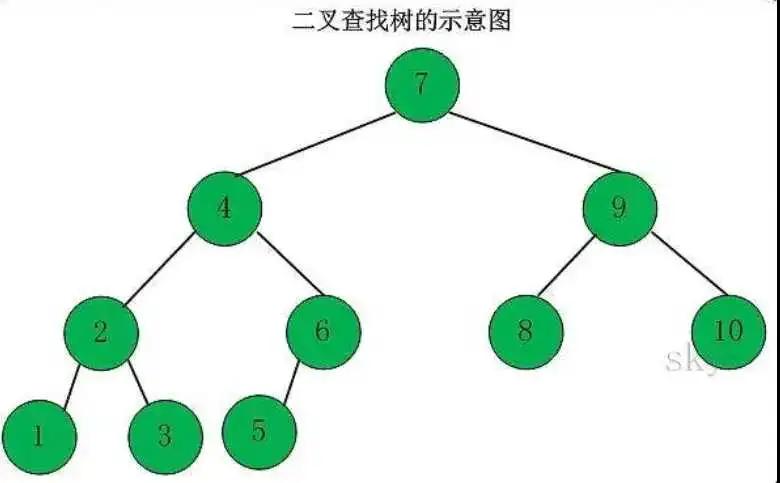
二叉搜索樹

二叉搜索樹，它是一顆空樹，具有以下性質的二叉樹，稱之為二叉搜索樹

1. 它的左子樹不為空，并且左子樹的所有節點值都要小于跟節點的值。
2. 它的右子樹不為空，則右子樹的所有節點的值都要大于跟節點的值。
3. 它的左右子樹分別為二叉排序樹。

平衡二叉樹

平衡二叉樹具有以下性質 他是一顆控訴或者他的左右兩個子樹的高度差絕對值不超過1，并且左右兩個子樹都是一顆平衡二叉樹。平衡二叉樹實現有紅黑樹，AVL，伸展樹，最小二叉平衡樹的節點公示為：F(n)=F(n-1)+F(n-2)+1

B-樹

一顆m階B樹，是一顆平衡的m路搜索樹，或者是空樹，滿足以下性質

1. 1根節點至少有兩個子女
2. 每個非跟節點包含k-1個元素和k個孩子，其中m/2 <= k <= m
3. 所有的葉子結點都位于同一層。
4. 每個節點中的元素從小到大排列，節點當中k-1個元素正好是k個孩子包含的元素值域的劃分一般用于文件系統或者數據庫的索引

一般用于文件系統或者數據庫的索引

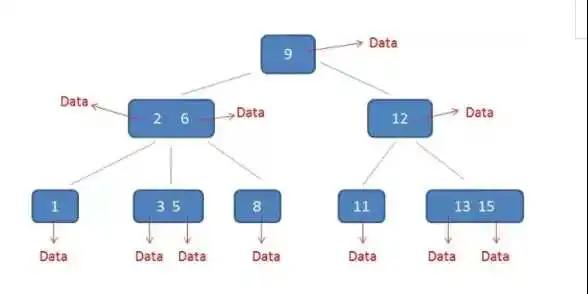
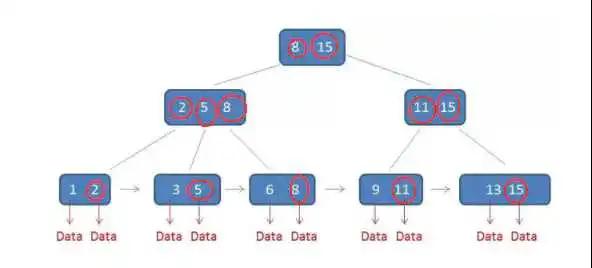
B+樹

B+樹具有以下特點

1. 有k個子樹的中間節點包含k個元素，每個元素不保存數據，只用來保存索引，所有數據保存在葉子節點。
2. 所有的葉子節點中包含了全部的元素信息，以及指向這些元素信息的執政，并且葉子節點本身也是按照由大到小依次排列。
3. 所有的中間節點元素都保存在葉子節點，在子元素中總是最大或者最小的元素。

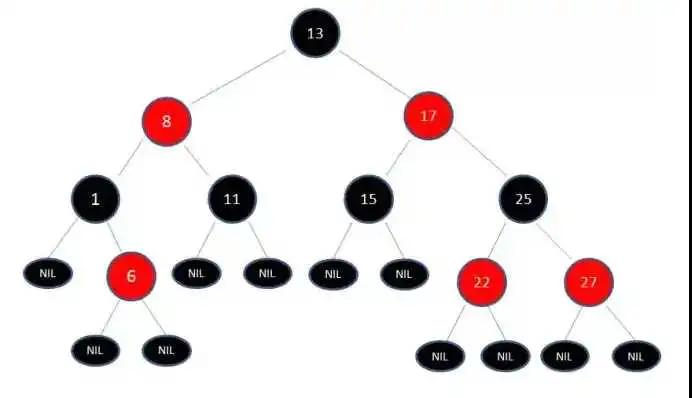
紅黑樹

紅黑樹是平衡二叉樹的實現，具有以下特征

1. 節點是紅色或者是黑色。
2. 根節點時黑色。
3. 每個葉子節點都是黑色節點的空節點
4. 每個紅色節點的兩個子節點都是黑色，從每個葉子節點到根的所有路徑上不能有兩個連續的紅色節點
5. 從任意節點到每個葉子節點所有的路徑都包含相同數目的黑色節點。