大O符號和代碼效率:花最少的精力得到最大的產出
本文轉載自公眾號“讀芯術”(ID:AI_Discovery)。
首先,什么是代碼效率?這個熱門術語在各種會議、講座和博客中已經被用濫了。它被廣泛用于描述代碼的速度和可靠性,與軟件的算法效率和運行時執行速度密切相關。在當下,這個人工智能、可擴展性和機器學習處于軟件開發前沿的時代,這個話題始終被反復提及。
那么什么是大O符號呢?在計算機科學領域中,它是用來描述算法的性能和效率以及分析整體性能的工具,被用于確定完成算法執行所需時間或空間的最壞情況。大O符號是基于性能來確定函數最佳實現的寶貴工具,它提供了一種正式的說法,用于討論算法的運行時間如何根據輸入而變化。
時間復雜度vs空間復雜度
大O符號用于度量時間復雜度和空間復雜度。
- 時間復雜度:為完成整體操作而必須執行的小操作的數量。
- 空間復雜度:運行算法中的代碼所需的額外內存量——通常被稱為輔助空間復雜度,也就是說它僅指代算法所占用的空間,不包括輸入所占用的空間。
復雜度類型
時間復雜度可以分為幾種不同的類型。下列是幾種較常見類型:
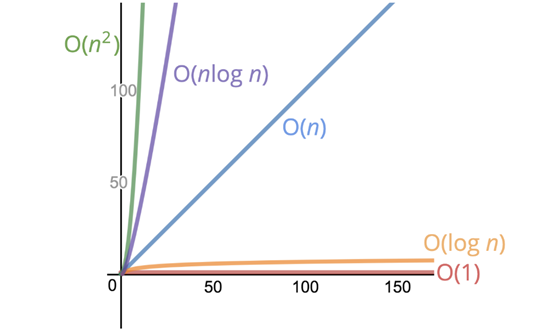
- 常數階/O(1):無論數據集多大,始終在相同的時間或空間中執行。
- 對數階/O(log n):為獲得給定數據,固定數據所必須增加的冪。
- 線性階/ O(n):復雜度與輸入數據的大小直接相關。
- 線性對數階/ O(nlog n):對輸入中的每一項執行O(log n)操作。
- 平方階/O(n²):性能與輸入數據的平方大小成正比。
圖源:Colt Steele的JavaScript算法和數據結構大師班
有助于確定時空復雜度的一般規則
這些規則是可以起作用的方向,但不保證每次都有效果。
確定時間復雜度:
- 算術運算恒定
- 變量賦值為常數
- 數組(通過索引)或對象(通過鍵)中的訪問元素是常量
- 在循環中,復雜度是循環的長度乘以循環內發生的任何事情的復雜度。
確定空間復雜度:
- 大多數基元是常量空間。(布爾常量,數字,未定義變量,空。)
- 字符串需要O(n)空間,其中n是字符串的長度。
- 引用類型通常為O(n),其中n是對象的數組長度或鍵數。
來看一些例子
圖源:Colt Steele的JavaScript算法和數據結構大師班
至于空間復雜度,addUpToN有2個變量賦值(total和i)。當循環完成其操作時,這些變量會被重新分配,但無論輸入數據集的大小如何,這些變量占用的空間都保持不變。空間復雜度將為常數階/O(1)。
這里有3個簡單的運算(乘、加、除)。不管n的大小如何,操作的數量保持不變。addUpToNAgain的時間復雜度為常數階/O(1)。
此時只會返回一個值。輸入值不會改變分配給此函數的空間。因此,空間復雜度也是線性階/O(1)。
在這里,有一個線性階O(n)運算嵌套在另一個O(n)運算中。當輸入的n值縮放時,運行時間隨之發生變動。sumEachPair的時間復雜度是平方階/O(n²)。
回顧一下前文所述的一般規則,這個案例正好對應了其中一條:引用類型一般是O(n),其所需的空間量與輸入值直接相關。空間復雜度則為線性階/O(n)。
想分析算法的性能,可以使用大O符號幫助分析,大O符號可以加深對算法的時間和空間要求的理解。
總之,程序員要理解好所編寫的代碼的時空復雜度,進而確保運行時間和執行速度達到最快,同時保證代碼始終保持在其運行系統的實體存儲范圍內,“修煉”成一個高效的程序員。