什么叫回溯算法

對(duì)于回溯算法的定義，百度百科上是這樣描述的：回溯算法實(shí)際上一個(gè)類似枚舉的搜索嘗試過(guò)程，主要是在搜索嘗試過(guò)程中尋找問(wèn)題的解，當(dāng)發(fā)現(xiàn)已不滿足求解條件時(shí)，就“回溯”返回，嘗試別的路徑。回溯法是一種選優(yōu)搜索法，按選優(yōu)條件向前搜索，以達(dá)到目標(biāo)。但當(dāng)探索到某一步時(shí)，發(fā)現(xiàn)原先選擇并不優(yōu)或達(dá)不到目標(biāo)，就退回一步重新選擇，這種走不通就退回再走的技術(shù)為回溯法，而滿足回溯條件的某個(gè)狀態(tài)的點(diǎn)稱為“回溯點(diǎn)”。許多復(fù)雜的，規(guī)模較大的問(wèn)題都可以使用回溯法，有“通用解題方法”的美稱。

看明白沒(méi)，回溯算法其實(shí)就是一個(gè)不斷探索嘗試的過(guò)程，探索成功了也就成功了，探索失敗了就在退一步，繼續(xù)嘗試……，

組合總和

組合總和算是一道比較經(jīng)典的回溯算法題，其中有一道題是這樣的。

找出所有相加之和為 n 的 k 個(gè)數(shù)的組合。組合中只允許含有 1 - 9 的正整數(shù)，并且每種組合中不存在重復(fù)的數(shù)字。

說(shuō)明：

• 所有數(shù)字都是正整數(shù)。
• 解集不能包含重復(fù)的組合。

示例 1:

• 輸入: k = 3, n = 7
• 輸出: [[1,2,4]]

示例 2:

• 輸入: k = 3, n = 9
• 輸出: [[1,2,6], [1,3,5], [2,3,4]]

這題說(shuō)的很明白，就是從1-9中選出k個(gè)數(shù)字，他們的和等于n，并且這k個(gè)數(shù)字不能有重復(fù)的。所以第一次選擇的時(shí)候可以從這9個(gè)數(shù)字中任選一個(gè)，沿著這個(gè)分支走下去，第二次選擇的時(shí)候還可以從這9個(gè)數(shù)字中任選一個(gè)，但因?yàn)椴荒苡兄貜?fù)的，所以要排除第一次選擇的，第二次選擇的時(shí)候只能從剩下的8個(gè)數(shù)字中選一個(gè)……。這個(gè)選擇的過(guò)程就比較明朗了，我們可以把它看做一棵9叉樹(shù)，除葉子結(jié)點(diǎn)外每個(gè)節(jié)點(diǎn)都有9個(gè)子節(jié)點(diǎn)，也就是下面這樣

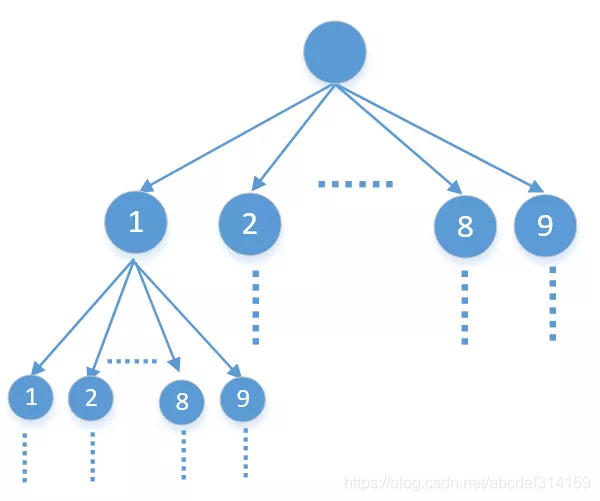
從9個(gè)數(shù)字中任選一個(gè)，就是沿著他的任一個(gè)分支一直走下去，其實(shí)就是DFS(如果不懂DFS的可以看下373，數(shù)據(jù)結(jié)構(gòu)-6,樹(shù))，二叉樹(shù)的DFS代碼是下面這樣的

public static void treeDFS(TreeNode root) { 
    if (root == null) 
        return; 
    System.out.println(root.val); 
    treeDFS(root.left);    treeDFS(root.right);} 

這里可以仿照二叉樹(shù)的DFS來(lái)寫(xiě)一下9叉樹(shù)，9叉樹(shù)的DFS就是通過(guò)遞歸遍歷他的9個(gè)子節(jié)點(diǎn)，代碼如下

public static void treeDFS(TreeNode root) { 
    //遞歸必須要有終止條件 
    if (root == null) 
        return; 
    System.out.println(root.val);    //通過(guò)循環(huán)，分別遍歷9個(gè)子樹(shù) 
    for (int i = 1; i <= 9; i++) { 
        //2，一些操作，可有可無(wú)，視情況而定 
        treeDFS("第i個(gè)子節(jié)點(diǎn)"); 
        //3，一些操作，可有可無(wú)，視情況而定 
    }} 

DFS其實(shí)就相當(dāng)于遍歷他的所有分支，就是列出他所有的可能結(jié)果，只要判斷結(jié)果等于n就是我們要找的，那么這棵9叉樹(shù)最多有多少層呢，因?yàn)橛衚個(gè)數(shù)字，所以最多只能有k層。來(lái)看下代碼

public List<List<Integer>> combinationSum3(int k, int n) { 
    List<List<Integer>> res = new ArrayList<>(); 
    dfs(res, new ArrayList<>(), k, 1, n); 
    return res; 
}private void dfs(List<List<Integer>> res, List<Integer> list, int k, int start, int n) { 
    //終止條件，如果滿足這個(gè)條件，再往下找也沒(méi)什么意義了 
    if (list.size() == k || n <= 0) { 
        //如果找到一組合適的就把他加入到集合list中 
        if (list.size() == k && n == 0) 
            res.add(new ArrayList<>(list)); 
        return; 
    } 
    //通過(guò)循環(huán)，分別遍歷9個(gè)子樹(shù) 
    for (int i = start; i <= 9; i++) { 
        //選擇當(dāng)前值 
        list.add(i); 
        //遞歸 
        dfs(res, list, k, i + 1, n - i); 
        //撤銷選擇 
        list.remove(list.size() - 1); 
    } 
} 

代碼相對(duì)來(lái)說(shuō)還是比較簡(jiǎn)單的，我們來(lái)分析下(如果看懂了可以直接跳過(guò))。

1. 代碼dfs中最開(kāi)始的地方是終止條件的判斷，之前在426，什么是遞歸，通過(guò)這篇文章，讓你徹底搞懂遞歸中講過(guò)，遞歸必須要有終止條件。
2. 下面的for循環(huán)分別遍歷他的9個(gè)子節(jié)點(diǎn)，注意這里的i是從start開(kāi)始的，所以有可能還沒(méi)有9個(gè)子樹(shù)，前面說(shuō)過(guò)，如果從9個(gè)數(shù)字中選擇一個(gè)之后，第2次就只能從剩下的8個(gè)選擇了，第3次就只能從剩下的7個(gè)中選擇了……
3. 在第20行dsf中的start是i+1，這里要說(shuō)一下為什么是i+1。比如我選擇了3，下次就應(yīng)該從4開(kāi)始選擇，如果不加1，下次還從3開(kāi)始就出現(xiàn)了數(shù)字重復(fù)，明顯與題中的要求不符
4. for循環(huán)的i為什么不能每次都從1開(kāi)始，如果每次都從1開(kāi)始就會(huì)出現(xiàn)結(jié)果重復(fù)，比如選擇了[1，2]，下次可能就會(huì)選擇[2，1]。
5. 如果對(duì)回溯算法不懂的，可能最不容易理解的就是最后一行，為什么要撤銷選擇。如果經(jīng)常看我公眾號(hào)的同學(xué)可能知道，也就是我經(jīng)常提到的分支污染問(wèn)題，因?yàn)閘ist是引用傳遞，當(dāng)從一個(gè)分支跳到另一個(gè)分支的時(shí)候，如果不把前一個(gè)分支的數(shù)據(jù)給移除掉，那么list就會(huì)把前一個(gè)分支的數(shù)據(jù)帶到下一個(gè)分支去，造成結(jié)果錯(cuò)誤(下面會(huì)講)。那么除了把前一個(gè)分支的數(shù)據(jù)給移除以外還有一種方式就是每個(gè)分支都創(chuàng)建一個(gè)list，這樣每個(gè)分支都是一個(gè)新的list，都不互相干擾，也就是下面圖中這樣

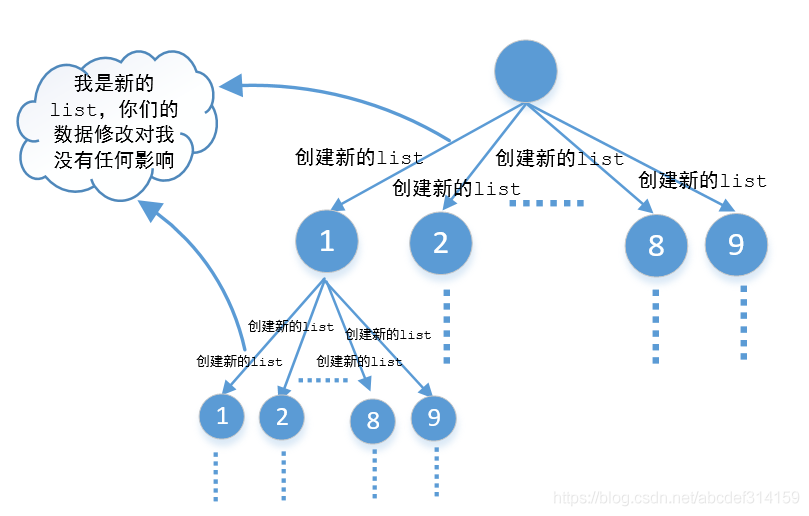
代碼如下

public List<List<Integer>> combinationSum3(int k, int n) { 
    List<List<Integer>> res = new ArrayList<>(); 
    dfs(res, new ArrayList<>(), k, 1, n); 
    return res; 
}private void dfs(List<List<Integer>> res, List<Integer> list, int k, int start, int n) { 
    //終止條件，如果滿足這個(gè)條件，再往下找也沒(méi)什么意義了 
    if (list.size() == k || n <= 0) { 
        //如果找到一組合適的就把他加入到集合list中 
        if (list.size() == k && n == 0) 
            res.add(new ArrayList<>(list)); 
        return; 
    } 
    //通過(guò)循環(huán)，分別遍歷9個(gè)子樹(shù) 
    for (int i = start; i <= 9; i++) { 
        //創(chuàng)建一個(gè)新的list，和原來(lái)的list撇清關(guān)系，對(duì)當(dāng)前l(fā)ist的修改并不會(huì)影響到之前的list 
        List<Integer> subList = new LinkedList<>(list); 
        subList.add(i); 
        //遞歸 
        dfs(res, subList, k, i + 1, n - i); 
        //注意這里沒(méi)有撤銷的操作，因?yàn)槭窃谝粋€(gè)新的list中的修改，原來(lái)的list并沒(méi)有修改， 
        //所以不需要撤銷操作 
    } 
} 

我們看到最后并沒(méi)有撤銷的操作，這是因?yàn)槊總€(gè)分支都是一個(gè)新的list，你對(duì)當(dāng)前分支的修改并不會(huì)影響到其他分支，所以并不需要撤銷操作。

注意：大家盡量不要寫(xiě)這樣的代碼，這種方式雖然也能解決，但每個(gè)分支都會(huì)重新創(chuàng)建list，效率很差。

要搞懂最后一行代碼首先要明白什么是遞歸，遞歸分為遞和歸兩部分，遞就是往下傳遞，歸就是往回走。遞歸你從什么地方調(diào)用最終還會(huì)回到什么地方去，我們來(lái)畫(huà)個(gè)簡(jiǎn)單的圖看一下

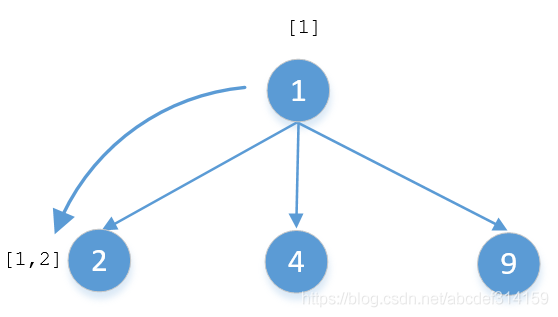
這是一棵非常簡(jiǎn)單的3叉樹(shù)，假如要對(duì)他進(jìn)行DFS遍歷，當(dāng)沿著1→2這條路徑走下去的時(shí)候，list中應(yīng)該是[1，2]。因?yàn)槭沁f歸調(diào)用最終還會(huì)回到節(jié)點(diǎn)1，如果不把2給移除掉，當(dāng)沿著1→4這個(gè)分支走下去的時(shí)候就變成[1，2，4]，但實(shí)際上1→4這個(gè)分支的結(jié)果應(yīng)該是[1，4]，這是因?yàn)槲覀儼亚耙粋€(gè)分支的值給帶過(guò)來(lái)了。當(dāng)1，2這兩個(gè)節(jié)點(diǎn)遍歷完之后最終還是返回節(jié)點(diǎn)1，在回到節(jié)點(diǎn)1的時(shí)候就應(yīng)該把結(jié)點(diǎn)2的值給移除掉，讓list變?yōu)閇1]，然后再沿著1→4這個(gè)分支走下去，結(jié)果就是[1，4]。

我們來(lái)總結(jié)一下回溯算法的代碼模板吧

private void backtrack("原始參數(shù)") { 
    //終止條件(遞歸必須要有終止條件) 
    if ("終止條件") { 
        //一些邏輯操作（可有可無(wú)，視情況而定） 
        return; 
    }    for (int i = "for循環(huán)開(kāi)始的參數(shù)"; i < "for循環(huán)結(jié)束的參數(shù)"; i++) { 
        //一些邏輯操作（可有可無(wú)，視情況而定） 
        //做出選擇 
        //遞歸 
        backtrack("新的參數(shù)"); 
        //一些邏輯操作（可有可無(wú)，視情況而定） 
        //撤銷選擇 
    } 
} 

有了模板，回溯算法的代碼就非常容易寫(xiě)了，下面就根據(jù)模板來(lái)寫(xiě)幾個(gè)經(jīng)典回溯案例的答案。

八皇后問(wèn)題

八皇后問(wèn)題也是一道非常經(jīng)典的回溯算法題，前面也有對(duì)八皇后問(wèn)題的專門介紹，有不明白的可以先看下394，經(jīng)典的八皇后問(wèn)題和N皇后問(wèn)題。他就是不斷的嘗試，如果當(dāng)前位置能放皇后就放，一直到最后一行如果也能放就表示成功了，如果某一個(gè)位置不能放，就回到上一步重新嘗試。比如我們先在第1行第1列放一個(gè)皇后，如下圖所示

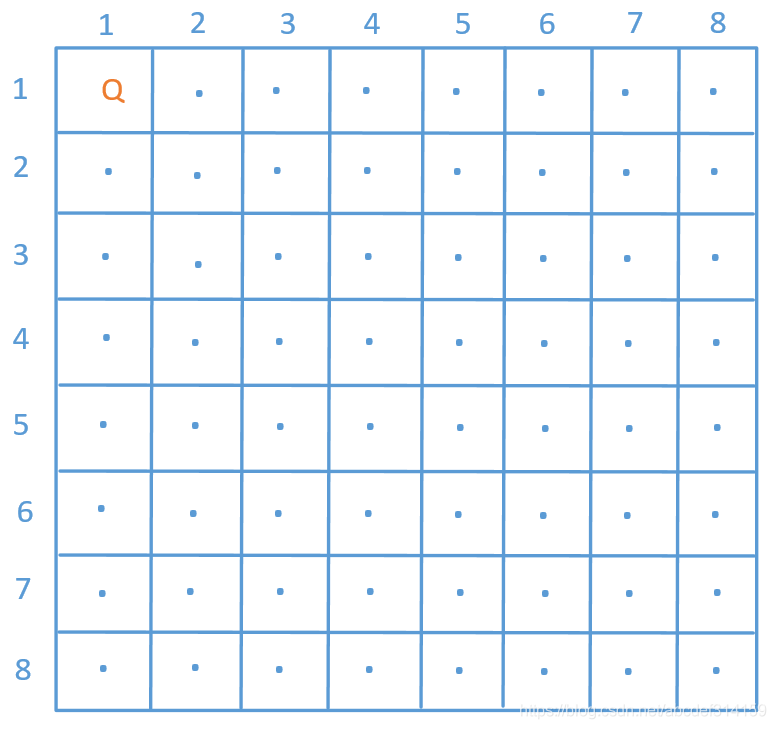
然后第2行從第1列開(kāi)始在不沖突的位置再放一個(gè)皇后，然后第3行……一直這樣放下去，如果能放到第8行還不沖突說(shuō)明成功了，如果沒(méi)到第8行的時(shí)候出現(xiàn)了沖突就回到上一步繼續(xù)查找合適的位置……來(lái)看下代碼

//row表示的是第幾行 
public void solve(char[][] chess, int row) { 
    //終止條件，row是從0開(kāi)始的，最后一行都可以放，說(shuō)明成功了    if (row == chess.length) {        //自己寫(xiě)的一個(gè)公共方法，打印二維數(shù)組的，        //主要用于測(cè)試數(shù)據(jù)用的        Util.printTwoCharArrays(chess);        System.out.println();        return;    }    for (int col = 0; col < chess.length; col++) { 
        //驗(yàn)證當(dāng)前位置是否可以放皇后 
        if (valid(chess, row, col)) { 
            //如果在當(dāng)前位置放一個(gè)皇后不沖突， 
            //就在當(dāng)前位置放一個(gè)皇后 
            chess[row][col] = 'Q'; 
            //遞歸，在下一行繼續(xù)…… 
            solve(chess, row + 1); 
            //撤銷當(dāng)前位置的皇后 
            chess[row][col] = '.'; 
        } 
    } 
} 

全排列問(wèn)題

給定一個(gè)沒(méi)有重復(fù)數(shù)字的序列，返回其所有可能的全排列。

• 示例:
• 輸入: [1,2,3]
• 輸出:

[  
[1,2,3],  
[1,3,2],  
[2,1,3],  
[2,3,1],  
[3,1,2],  
[3,2,1]  
] 

這道題我們可以把它當(dāng)做一棵3叉樹(shù)，所以每一步都會(huì)有3種選擇，具體過(guò)程就不在分析了，直接根據(jù)上面的模板來(lái)寫(xiě)下代碼

public List<List<Integer>> permute(int[] nums) { 
    List<List<Integer>> list = new ArrayList<>(); 
    backtrack(list, new ArrayList<>(), nums); 
    return list; 
}private void backtrack(List<List<Integer>> list, List<Integer> tempList, int[] nums) { 
    //終止條件 
    if (tempList.size() == nums.length) { 
        //說(shuō)明找到一一組組合 
        list.add(new ArrayList<>(tempList)); 
        return; 
    } 
    for (int i = 0; i < nums.length; i++) { 
        //因?yàn)椴荒苡兄貜?fù)的，所以有重復(fù)的就不能選 
        if (tempList.contains(nums[i])) 
            continue; 
        //選擇當(dāng)前值 
        tempList.add(nums[i]); 
        //遞歸 
        backtrack(list, tempList, nums); 
        //撤銷選擇 
        tempList.remove(tempList.size() - 1); 
    } 
} 

是不是感覺(jué)很簡(jiǎn)單。

子集問(wèn)題

給定一組不含重復(fù)元素的整數(shù)數(shù)組 nums，返回該數(shù)組所有可能的子集(冪集)。

• 說(shuō)明：解集不能包含重復(fù)的子集。
• 示例:
• 輸入: nums = [1,2,3]
• 輸出:

輸入: nums = [1,2,3] 
輸出: 
[ 
[3], 
[1], 
[2], 
[1,2,3], 
[1,3], 
[2,3], 
[1,2], 
[] 
] 

我們還是根據(jù)模板來(lái)修改吧

public List<List<Integer>> subsets(int[] nums) { 
    List<List<Integer>> list = new ArrayList<>(); 
    //先排序 
    Arrays.sort(nums); 
    backtrack(list, new ArrayList<>(), nums, 0); 
    return list; 
} 
private void backtrack(List<List<Integer>> list, List<Integer> tempList, int[] nums, int start) { 
    //注意這里沒(méi)有寫(xiě)終止條件，不是說(shuō)遞歸一定要有終止條件的嗎，這里怎么沒(méi)寫(xiě)，其實(shí)這里的終止條件 
    //隱含在for循環(huán)中了，當(dāng)然我們也可以寫(xiě)if(start>nums.length) rerurn;只不過(guò)這里省略了。 
    list.add(new ArrayList<>(tempList)); 
    for (int i = start; i < nums.length; i++) { 
        //做出選擇 
        tempList.add(nums[i]); 
        //遞歸 
        backtrack(list, tempList, nums, i + 1); 
        //撤銷選擇 
        tempList.remove(tempList.size() - 1); 
    } 
} 

所以類似這種題基本上也就是這個(gè)套路，就是先做出選擇，然后遞歸，最后再撤銷選擇。在講第一道示例的時(shí)候提到過(guò)撤銷的原因是防止把前一個(gè)分支的結(jié)果帶到下一個(gè)分支造成結(jié)果錯(cuò)誤。不過(guò)他們不同的是，一個(gè)是終止條件的判斷，還一個(gè)就是for循環(huán)的起始值，這些都要具體問(wèn)題具體分析。下面再來(lái)看最后一到題解數(shù)獨(dú)。

解數(shù)獨(dú)

數(shù)獨(dú)大家都玩過(guò)吧，他的規(guī)則是這樣的

一個(gè)數(shù)獨(dú)的解法需遵循如下規(guī)則：

• 數(shù)字 1-9 在每一行只能出現(xiàn)一次。
• 數(shù)字 1-9 在每一列只能出現(xiàn)一次。
• 數(shù)字 1-9 在每一個(gè)以粗實(shí)線分隔的 3x3 宮內(nèi)只能出現(xiàn)一次。

過(guò)程就不在分析了，直接看代碼，代碼中也有詳細(xì)的注釋，這篇講的是回溯算法，這里主要看一下backTrace方法即可，其他的可以先不用看

//回溯算法 
public static boolean solveSudoku(char[][] board) { 
    return backTrace(board, 0, 0); 
}//注意這里的參數(shù)，row表示第幾行，col表示第幾列。private static boolean backTrace(char[][] board, int row, int col) { 
    //注意row是從0開(kāi)始的，當(dāng)row等于board.length的時(shí)候表示數(shù)獨(dú)的 
    //最后一行全部讀遍歷完了，說(shuō)明數(shù)獨(dú)中的值是有效的，直接返回true 
    if (row == board.length) 
        return true; 
    //如果當(dāng)前行的最后一列也遍歷完了，就從下一行的第一列開(kāi)始。這里的遍歷    //順序是從第1行的第1列一直到最后一列，然后第二行的第一列一直到最后 
    //一列，然后第三行的……    if (col == board.length) 
        return backTrace(board, row + 1, 0); 
    //如果當(dāng)前位置已經(jīng)有數(shù)字了，就不能再填了，直接到這一行的下一列    if (board[row][col] != '.') 
        return backTrace(board, row, col + 1); 
    //如果上面條件都不滿足，我們就從1到9中選擇一個(gè)合適的數(shù)字填入到數(shù)獨(dú)中 
    for (char i = '1'; i <= '9'; i++) { 
        //判斷當(dāng)前位置[row，col]是否可以放數(shù)字i，如果不能放再判斷下        //一個(gè)能不能放，直到找到能放的為止，如果從1-9都不能放，就會(huì)下面 
        //直接return false 
        if (!isValid(board, row, col, i)) 
            continue;        //如果能放數(shù)字i，就把數(shù)字i放進(jìn)去        board[row][col] = i;        //如果成功就直接返回，不需要再嘗試了        if (backTrace(board, row, col)) 
            return true; 
        //否則就撤銷重新選擇        board[row][col] = '.'; 
    }    //如果當(dāng)前位置[row，col]不能放任何數(shù)字，直接返回false 
    return false; 
}//驗(yàn)證當(dāng)前位置[row，col]是否可以存放字符cprivate static boolean isValid(char[][] board, int row, int col, char c) { 
    for (int i = 0; i < 9; i++) { 
        if (board[i][col] != '.' && board[i][col] == c) 
            return false; 
        if (board[row][i] != '.' && board[row][i] == c) 
            return false; 
        if (board[3 * (row / 3) + i / 3][3 * (col / 3) + i % 3] != '.' && 
                board[3 * (row / 3) + i / 3][3 * (col / 3) + i % 3] == c) 
            return false; 
    }    return true; 
} 

總結(jié)

回溯算法要和遞歸結(jié)合起來(lái)就很好理解了，遞歸分為兩部分，第一部分是先往下傳遞，第二部分到達(dá)終止條件的時(shí)候然后再反彈往回走，我們來(lái)看一下階乘的遞歸

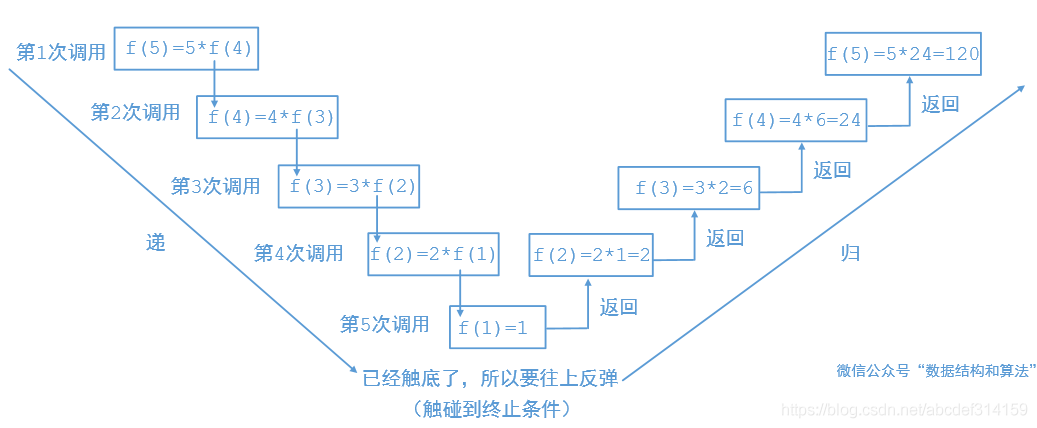
其實(shí)回溯算法就是在往下傳遞的時(shí)候把某個(gè)值給改變，然后往回反彈的時(shí)候再把原來(lái)的值復(fù)原即可。比如八皇后的時(shí)候我們先假設(shè)一個(gè)位置可以放皇后，如果走不通就把當(dāng)前位置給撤銷，放其他的位置。如果是組合之類的問(wèn)題，往下傳遞的時(shí)候我們把當(dāng)前值加入到list中，然后往回反彈的時(shí)候在把它從list中給移除掉即可。