[[337333]]

最新發布的《Java開發手冊(嵩山版)》增加了前后端規約，其中有一條：禁止服務端在超大整數下使用Long類型作為返回。這是為何?在實際開發中可能出現什么問題?本文從IEEE754浮點數標準講起，詳細解析背后的原理，幫助大家徹底理解這個問題，提前避坑。

8月3日，這個在我等碼農心中具有一定紀念意義的日子里，《Java開發手冊》發布了嵩山版。每次發布我都特別期待，因為總能找到一些程序員不得不重視的“血淋淋的巨坑”。比如這次，嵩山版中新增的模塊——前后端規約，其中一條禁止服務端在超大整數下使用Long類型作為返回。

這個問題，我在實際開發中遇到過，所以印象也特別深。如果在業務初期沒有評估到這一點，將訂單ID這類關鍵信息，按照Long類型返回給前端，可能會在業務中后期高速發展階段，突然暴雷，導致嚴重的業務故障。期望大家能夠重視。

這條規約給出了直接明確的避坑指導，但要充分理解背后的原理，知其所以然，還有很多點要思考。首先，我們來看幾個問題，如果能說出所有問題的細節，就可直接跳過了，否則下文還是值得一看的：

• 一問：JS的Number類型能安全表達的最大整型數值是多少?為什么(注意要求更嚴，是安全表達)?
• 二問：在Long取值范圍內，2的指數次整數轉換為JS的Number類型，不會有精度丟失，但能放心使用么?
• 三問：我們一般都知道十進制數轉二進制浮點數有可能會出現精度丟失，但精度丟失具體怎么發生的?
• 四問：如果不幸中招，服務端正在使用Long類型作為大整數的返回，有哪些辦法解決?

基礎回顧

在解答上面這些問題前，先介紹本文涉及到的重要基礎：IEEE754浮點數標準。如果大家對IEEE754的細節爛熟于心的話，可以跳過本段內容，直接看下一段，問題解答部分。

當前業界流行的浮點數標準是IEEE754，該標準規定了4種浮點數類型:單精度、雙精度、延伸單精度、延伸雙精度。前兩種類型是最常用的。我們單介紹一下雙精度，掌握雙精度，自然就了解了單精度(而且上述問題場景也是涉及雙精度)。

雙精度分配了8個字節，總共64位，從左至右劃分是1位符號、11位指數、52位有效數字。如下圖所示，以0.7為例，展示了雙精度浮點數的存儲方式。

存儲位分配

1)符號位：在最高二進制位上分配1位表示浮點數的符號，0表示正數，1表示負數。

2)指數：也叫階碼位。

在符號位右側分配11位用來存儲指數，IEEE754標準規定階碼位存儲的是指數對應的移碼，而不是指數的原碼或補碼。根據計算機組成原理中對移碼的定義可知，移碼是將一個真值在數軸上正向平移一個偏移量之后得到的，即[x]移=x+2^(n-1)(n為x的二進制位數，含符號位)。移碼的幾何意義是把真值映射到一個正數域，其特點是可以直觀地反映兩個真值的大小，即移碼大的真值也大。基于這個特點，對計算機來說用移碼比較兩個真值的大小非常簡單，只要高位對齊后逐個比較即可，不用考慮負號的問題，這也是階碼會采用移碼表示的原因所在。

由于階碼實際存儲的是指數的移碼，所以指數與階碼之間的換算關系就是指數與它的移碼之間的換算關系。假設指數的真值為e，階碼為E ，則有 E = e + (2 ^ (n-1) - 1)，其中 2 ^ (n-1) - 1 是IEEE754 標準規定的偏移量。則雙精度下，偏移量為1023，11位二進制取值范圍為[0，2047]，因為全0是機器零、全1是無窮大都被當做特殊值處理，所以E的取值范圍為[1,2046]，減去偏移量，可得e的取值范圍為[-1022,1023] 。

3)有效數字：也叫尾數位。最右側分配連續的52位用來存儲有效數字，IEEE754標準規定尾數以原碼表示。

浮點數和十進制之間的轉換

在實際實現中，浮點數和十進制之間的轉換規則有3種情況：

1 規格化

指數位不是全零，且不是全1時，有效數字最高位前默認增加1，不占用任何比特位。那么，轉十進制計算公式為：

(-1)^s*(1+m/2^52)*2^(E-1023) 

其中s為符號，m為尾數，E為階碼。比如上圖中的0.7 :

1)符號位：是0，代表正數。

2)指數位：01111111110，轉換為十進制，得階碼E為1022，則真值e=1022-1023=-1。

3)有效數字：

0110011001100110011001100110011001100110011001100110 

轉換為十進制，尾數m為：1801439850948198。

4)計算結果：

(1+1801439850948198/2^52)*(2^-1) =0.6999999999999999555910790149937383830547332763671875

經過顯示優化算法后(在后文中詳述)，為0.7。

2 非規格化

指數位是全零時，有效數字最高位前默認為0。那么，轉十進制計算公式：

(-1)^s*（0+m/2^52)*2^(-1022) 

注意，指數位是-1022，而不是-1023，這是為了平滑有效數字最高位前沒有1。比如非規格最小正值為：

0x0.0000000000001*2^-1022=2^-52 * 2^-1022 = 4.9*10^-324 

3 特殊值

指數全為1，有效數字全為0時，代表無窮大;有效數字不為0時，代表NaN(不是數字)。

問題解答

1 JS的Number類型能安全表達的最大整型數值是多少?為什么?

規約中已經指出：

在Long類型能表示的最大值是2的63次方-1，在取值范圍之內，超過2的53次方(9007199254740992)的數值轉化為JS的Number時，有些數值會有精度損失。

“2的53次方”這個限制是怎么來的呢?如果看懂上文IEEE754基礎回顧，不難得出：在浮點數規格化下，雙精度浮點數的有效數字有52位，加上有效數字最高位前默認為1，共53位，所以JS的Number能保障無精度損失表達的最大整數是2的53次方。

而這里的題問是：“能安全表達的最大整型”，安全表達的要求，除了能準確表達，還有正確比較。2^53=9007199254740992，實際上，

9007199254740992+1 == 9007199254740992 

的比較結果為true。如下圖所示：

這個測試結果足以說明2^53不是一個安全整數，因為它不能唯一確定一個自然整數，實際上9007199254740992、9007199254740993，都對應這個值。因此這個問題的答案是：2^53-1。

2 在Long取值范圍內，2的指數次整數轉換為JS的Number類型，不會有精度丟失，但能放心使用么?

規約中指出：

在Long取值范圍內，任何2的指數次整數都是絕對不會存在精度損失的，所以說精度損失是一個概率問題。若浮點數尾數位與指數位空間不限，則可以精確表示任何整數。

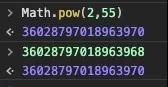
后半句，我們就不說了，因為絕對沒毛病，空間不限，不僅是任何整數可以精確表示，無理數我們也可以挑戰一下。我們重點看前半句，根據本文前面所述基礎回顧，雙精度浮點數的指數取值范圍為[-1022,1023]，而指數是以2為底數。另外，雙精度浮點數的取值范圍，比Long大，所以，理論上Long型變量中2的指數次整數一定可以準確轉換為JS的umber類型。但在JS中，實際情況，卻是下面這樣：

2的55次方的準確計算結果是：36028797018963968，而從上圖可看到，JS的計算結果是：36028797018963970。而且直接輸入36028797018963968，控制臺顯示結果是36028797018963970。

這個測試結果，已經對本問題給出答案。為了確保程序準確，本文建議，在整數場景下，對于JS的Number類型使用，嚴格限制在2^53-1以內，最好還是信規約的，直接使用String類型。

為什么會出現上面的測試現象呢?

實際上，我們在程序中輸入一個浮點數a，在輸出得到a'，會經歷以下過程：

1)輸入時：按照IEEE754規則，將a存儲。這個過程很有可能會發生精度損失。

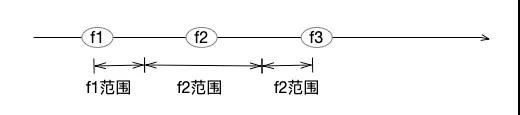
2)輸出時：按照IEEE754規則，計算a對應的值。根據計算結果，尋找一個最短的十進制數a'，且要保障a'不會和a隔壁浮點數的范圍沖突。a隔壁浮點數是什么意思呢?由于存儲位數是限定的，浮點數其實是一個離散的集合，兩個緊鄰的浮點數之間，還存在著無數的自然數字，無法表達。假設有f1、f2、f3三個升序浮點數，且它們之間的距離，不可能在拉近。則在這三個浮點數之間，按照范圍來劃分自然數。而浮點數輸出的過程，就是在自己范圍中找一個最適合的自然數，作為輸出。如何找到最合適的自然數，這是一個比較復雜的浮點數輸出算法，大家感興趣的，可參考相關論文[1]。

所以，36028797018963968和36028797018963970這兩個自然數，對應到計算機浮點數來說，其實是同一個存儲結果，雙精度浮點數無法區分它們，最終呈現哪一個十進制數，就看浮點數的輸出算法了。下圖這個例子可以說明這兩個數字在浮點數中是相等的。另外，大家可以想想輸入0.7,輸出是0.7的問題，浮點數是無法精確存儲0.7，輸出卻能夠精確，也是因為有浮點數輸出算法控制(特別注意，這個輸出算法無法保證所有情況下，輸入等于輸出，它只是盡力確保輸出符合正常的認知)。

擴展

JS的Number類型既用來做整數計算、也用來做浮點數計算。其轉換為String輸出的規則也會影響我們使用，具體規則如下：

上面是一段典型的又臭又長但邏輯很嚴謹的描述，我總結了一個不是很嚴謹，但好理解的說法，大家可以參考一下：

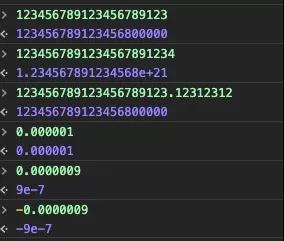
除了小數點前的數字位數(不算開始的0)少于22位，且絕對值大于等于1e-6的情況，其余都用科學計數法格式化輸出。舉例：

3 我們一般都知道十進制數轉二進制浮點數有可能會出現精度丟失，精度丟失怎么發生的?

通過前面IEEE754分析，我們知道十進制數存儲到計算機，需要轉換為二進制。有兩種情況，會導致轉換后精度損失：

1)轉換結果是無限循環數或無理數

比如0.1轉換成二進制為：

0.0001 10011001100110011001100110011... 

其中0011在循環。將0.1轉換為雙精度浮點數二進制存儲為：

0 01111111011 1001100110011001100110011001100110011001100110011001 

按照本文前面所述基礎回顧中的計算公式 (-1)^s*(1+m/2^52)*2^(E-1023)計算，可得轉換回十進制為：0.09999999999999999。這里可以看出，浮點數有時是無法精確表達一個自然數，這個和十進制中1/3 =0.333333333333333...是一個道理。

2)轉換結果長度，超過有效數字位數，超過部分會被舍棄

IEEE754默認是舍入到最近的值，如果“舍”和“入”一樣接近，那么取結果為偶數的選擇。

另外，在浮點數計算過程中，也可能引起精度丟失。比如，浮點數加減運算執行步驟分為：

零值檢測 -> 對階操作 -> 尾數求和 -> 結果規格化 -> 結果舍入

其中對階和規格化都有可能造成精度損失：

• 對階：是通過尾數右移(左移會導致高位被移出，誤差更大，所以只能是右移)，將小指數改成大指數，達到指數階碼對齊的效果，而右移出的位，會作為保護位暫存，在結果舍入中處理，這一步有可能導致精度丟失。
• 規格化：是為了保障計算結果的尾數最高位是1，視情況有可能會出現右規，即將尾數右移，從而導致精度丟失。

4 如果不幸中招，服務端正在使用Long類型作為大整數的返回，有哪些辦法解決?

需要分情況。

1)通過Web的ajax異步接口，以Json串的形式返回給前端

方案一：如果，返回Long型所在的POJO對象在其他地方無使用，那么可以將后端的Long型直接修改成String型。

方案二：如果，返回給前端的Json串是將一個POJO對象Json序列化而來，并且這個POJO對象還在其他地方使用，而無法直接將其中的Long型屬性直接改為String，那么可以采用以下方式：

String orderDetailString = JSON.toJSONString(orderVO, SerializerFeature.BrowserCompatible); 

SerializerFeature.BrowserCompatible 可以自動將數值變成字符串返回，解決精度問題。

方案三：如果，上述兩種方式都不適合，那么這種方式就需要后端返回一個新的String類型，前端使用新的，并后續上線后下掉老的Long型(推薦使用該方式，因為可以明確使用String型，防止后續誤用Long型)。

2)使用node的方式，直接通過調用后端接口的方式獲取

方案一：使用npm的js-2-java的 java.Long(orderId) 方法兼容一下。

方案二：后端接口返回一個新的String類型的訂單ID，前端使用新的屬性字段(推薦使用，防止后續踩坑)。

引用

[1]http://citeseerx.ist.psu.edu/viewdoc/summary?doi=10.1.1.52.2247&rank=2

[2]《碼出高效》