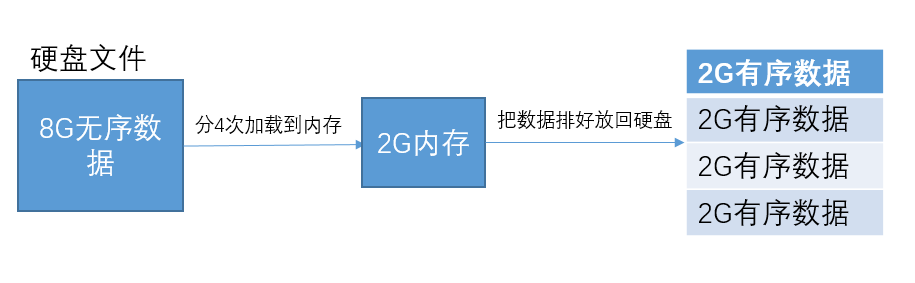
外部排序:如何用 2GB內(nèi)存給 20 億個整數(shù)排序?
這篇文章在很久很久之前講過,不過出了些小錯誤,今天把它修正了,并且從實戰(zhàn) + 漫畫的方式帶你領(lǐng)略外部排序魅力,并且讓你知道外部排序的實現(xiàn)方式?jīng)]有你想的那么簡單。
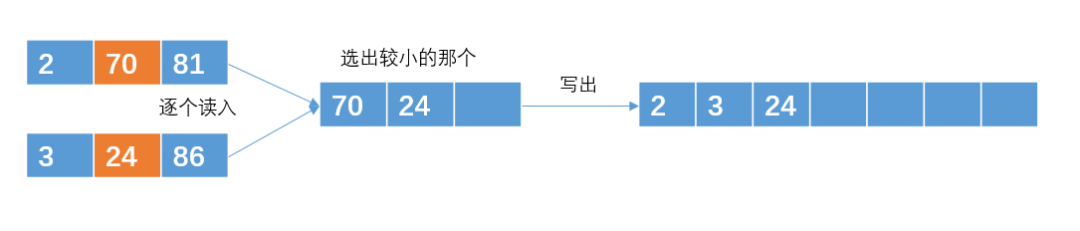
排序的時候我們可以選擇快速排序或歸并排序等算法。為了方便,我們把排序好的2G有序數(shù)據(jù)稱之為有序子串吧。接著我們可以把兩個小的有序子串合并成一個大的有序子串。
注意:讀取的時候是每次讀取一個int數(shù),通過比較之后在輸出。
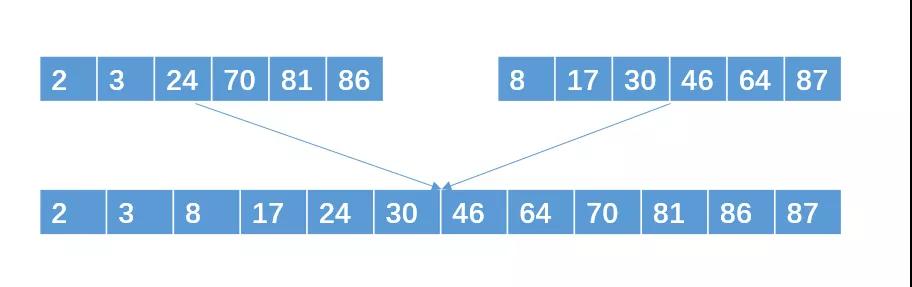
按照這個方法來回合并,總共經(jīng)過三次合并之后就可以得到8G的有序子串。
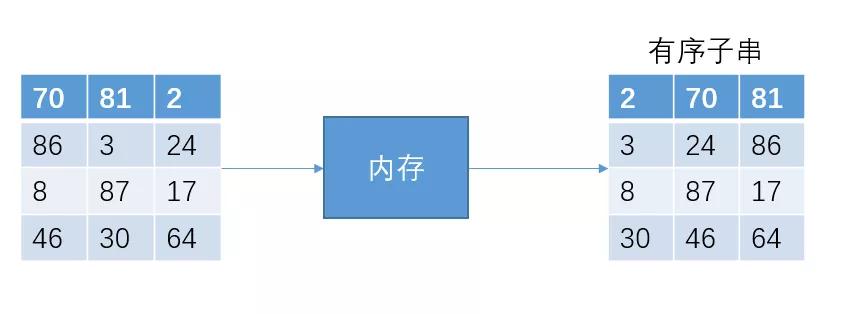
接下來把12個數(shù)據(jù)分成4份,然后排序成有序子串
然后把子串進(jìn)行兩兩合并
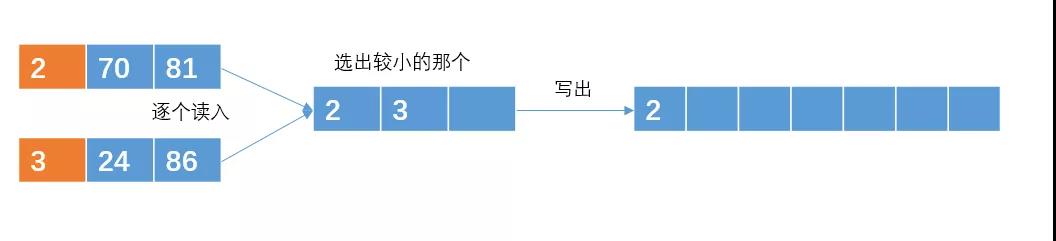
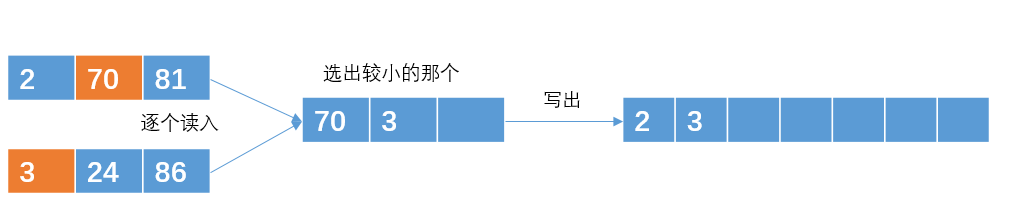
輸出哪個元素,就在那個元素所在的有序子串再次讀入一個元素
繼續(xù)
重復(fù)直到合并成一個包含6個int的有序子串
再把兩個包含6個int的有序子串合并成一個包含12個int數(shù)據(jù)的最終有序子串
優(yōu)化策略
解釋下:例如對于數(shù)據(jù)2,我們把無序的12個數(shù)據(jù)分成有序的4個子串需要讀寫各一次,把2份3個有序子串合并成6個有序子串讀寫各一次;把2份6個有序子串合并從12個有序子串讀寫各一次,一共需要讀寫各3次。
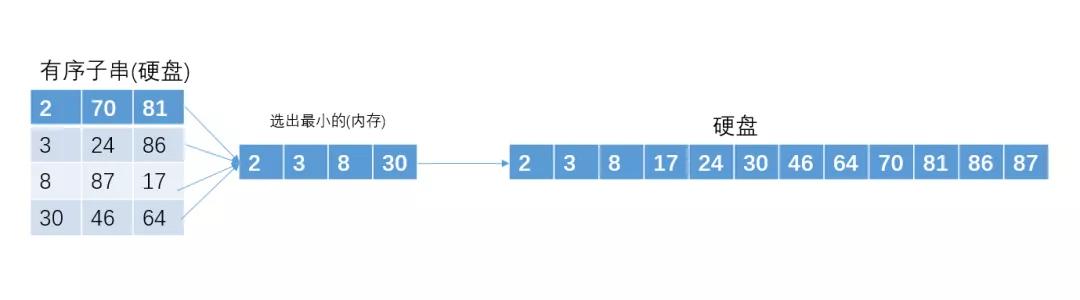
多路歸并
為了方便講解,我們假設(shè)內(nèi)存一共可以裝4個int型數(shù)據(jù)。
置換選擇
例如我們可以從12個數(shù)據(jù)讀取3個存到內(nèi)存中,然后從內(nèi)存中選出最小的那個數(shù)放進(jìn)子串p1里;
之后再從剩余的9個數(shù)據(jù)讀取一個放到內(nèi)存中,然后再從內(nèi)存中選出一個數(shù)放進(jìn)子串p1里,這個數(shù)必須滿足比p1中的其他數(shù)大,且在內(nèi)存中盡量小。
這樣一直重復(fù),直到內(nèi)存中的數(shù)都比p1中的數(shù)小,這時p1子串存放結(jié)束,繼續(xù)來p2子串的存放。例如(這時假設(shè)內(nèi)存只能存放3個int型數(shù)據(jù)):
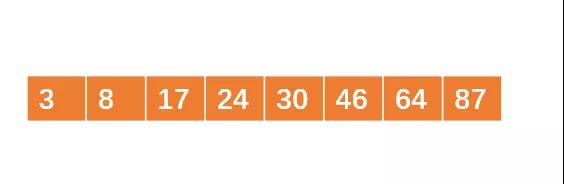
12個無序的int數(shù)據(jù)
讀入3個到內(nèi)存中,且選出一個最小的到子串p1
從內(nèi)存中再次讀取一個元素86
從內(nèi)存中再次讀取一個元素3
從內(nèi)存中再次讀取一個元素24
從內(nèi)存中再次讀取一個元素8
這個時候,已經(jīng)沒有符合要求的數(shù)了,且內(nèi)存已滿,進(jìn)而用p2子串來存放,以此類推。
通過這種方法,p1子串存放了4個數(shù)據(jù),而原來的那種方法p1子串只能存放3個數(shù)據(jù)。
(不知道堆排序的可以看下我之前寫的文章:【算法與數(shù)據(jù)結(jié)構(gòu)】堆排序是什么鬼?)
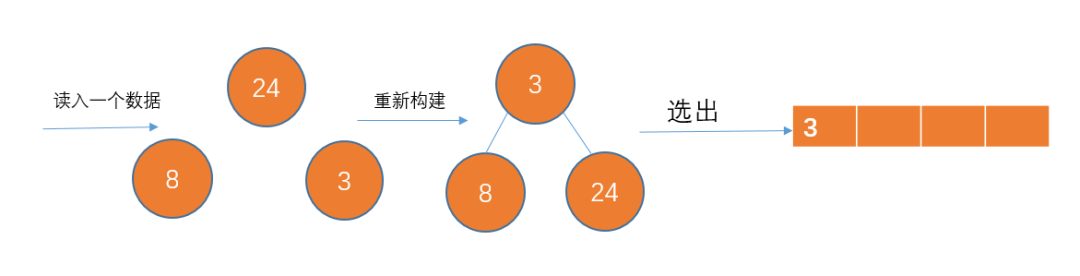
從12個數(shù)據(jù)中讀取3個數(shù)據(jù),構(gòu)建成一個最小堆,然后從堆頂選擇一個數(shù)寫入到p1中。
之后再從剩余的9個數(shù)中讀取一個數(shù),如果這個數(shù)比剛才那個寫入到p1中的數(shù)大,則把這個數(shù)插入到最小堆中,重新調(diào)整最小堆結(jié)構(gòu),然后在堆頂選一個數(shù)寫入到p1中。
否則,把這個數(shù)暫放在一邊,暫時不處理。之后一樣需要調(diào)整堆結(jié)構(gòu),從堆頂選擇一個數(shù)寫入到p1中。
這里說明一下,那個被放在一邊的數(shù)是不能再放入p1中的了,因為它一定比p1中的數(shù)都要小,所以它會放在下一個子串中
看這些文字會讓人頭大,我畫圖解釋下吧。
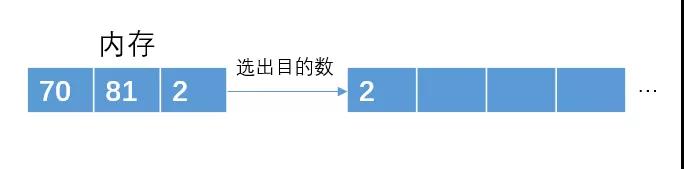
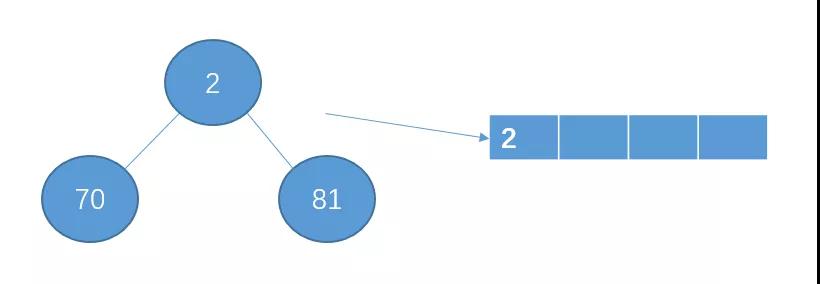
從12數(shù)據(jù)讀取3個數(shù)據(jù)
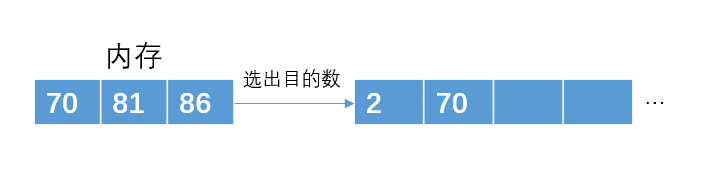
構(gòu)建最小堆,且選出目標(biāo)數(shù)
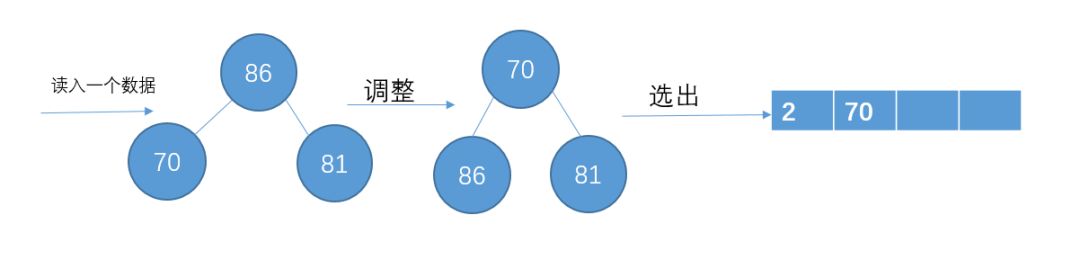
讀入下一個數(shù)86
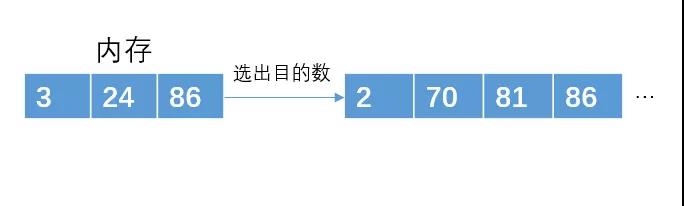
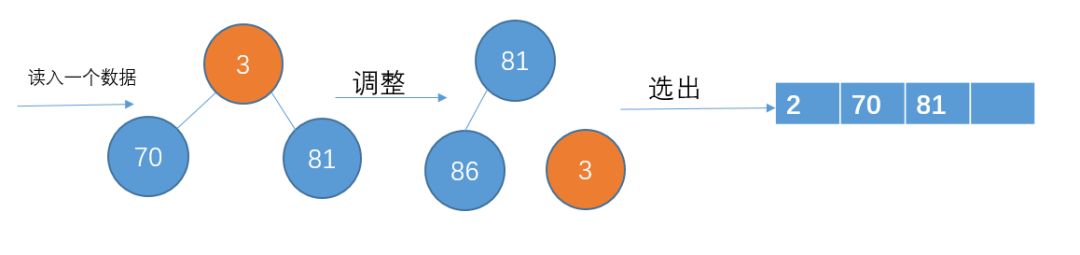
讀入下一個數(shù)3,比70小,暫放一邊,不加入堆結(jié)構(gòu)中
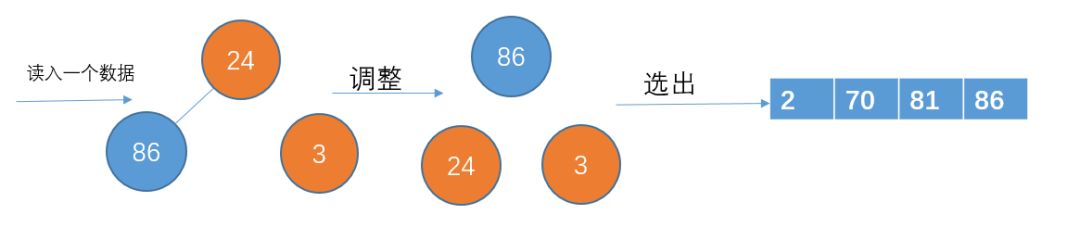
讀入下一個數(shù)據(jù)24,比81小,不加入堆結(jié)構(gòu)
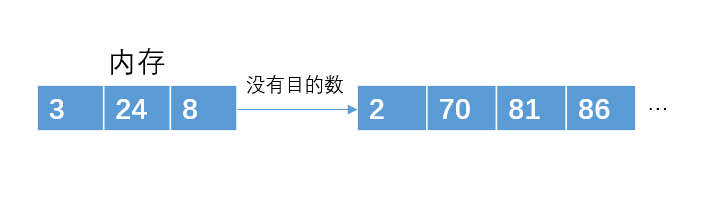
讀入下一個數(shù)據(jù)8,比86小,不加入堆結(jié)構(gòu)。此時p1已經(jīng)完成了,把那些剛才暫放一邊的數(shù)重新構(gòu)成一個堆,繼續(xù)p2的存放。
以此類推...
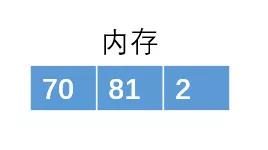
最后生成的p2如下:
這種方法適合要排序的數(shù)據(jù)太多,以至于內(nèi)存一次性裝載不下。只能通過把數(shù)據(jù)分幾次的方式來排序,我們也把這種方法稱之為外部排序