數據分析入門經典問題:你兩個朋友同一天過生日的概率有多大?
假如把N個人分成一組,至少有兩個人是同一天生日的概率是多少?
現在來猜一猜:假設這一組有N=30個人。那么有兩個人在同一天吃生日蛋糕的概率是多少呢?我們換個說法:你敢不敢用10美元賭里面有兩個同月同日生的人?
我們會以這個例子收尾,但首先我們需要收集所有的元件(也就是下文標題部分),才能解開生日謎題。
基礎中的基礎
為了充分“賣弄學問”,我們就略去惹人白眼的引言部分:概率的數值在0和1 之間(如果喜歡的話,你還可以說它在0%到100%之間)。好的。現在你明白為什么“我1000%確定他們會遲到”一類句子會讓數據猿急得跳腳。
分析概率的三種方式
人們在分析概率時,常用三種方法:
- 基于事件的概率(包括列舉事件,計算事件數量)
- 基于頻率的概率(包括用代表事物在平行宇宙中的收束方式的分布)
- 主觀概率(包括代表人對于可能發生情況的信念的分布,尤指通過賭注的方式……畢竟不空口說白話可以避免胡說八道)
假如你的統計課老師沒有一字一句地強調基礎要點,那筆者告訴你,課本將提到以下內容:
基于事件的概率
概率=[分子]/[分母]
前幾章會從基于事件的概率分析方法開始。因為通過這種方法人們能很容易地就獲取到基本信息,而且或許大部分人(你懂的)已經有這方面的直覺。舉個例子:投擲一枚硬幣背面朝上的概率是?1/2. 投擲骰子出現6點的概率是多少?1/6.為什么會這樣?
分子:所考察的事件可能發生的次數
分母:任何(有關)事件發生的次數
就一枚硬幣來說,分母即所有相關事件是正面朝上和背面朝上。這就是分母2的來源。很簡單。
細數事件
要想處理基于事件的概率問題,我們首先需要列舉出所有的事件并記錄事件的數量。這也就是為什么教材很可能會不停地講如何組合分析,直到你徹底看煩。組合分析能教你掌握計算(針對所求分子和分母的)事件數量的方法。
回顧在作業中出現無數遍的問題,無非是關于:“從100名候選人中選出19名委員有多少種方式?”(17310309456440種)或者是“一組4位數密碼共有多少種組合可能?”(1000種)。
在基于事件的世界里,所有的時間群發生的概率相等,因而它們在算法中不受各個層的凌亂的調節器影響。在這個世界里,拋出去的每枚硬幣的正反面朝上的概率相當,所有投擲的骰子出現的數字平衡,所有的卡牌都無需重排,所有的人的出生日期的分布均等。
對于生日問題,我們需要快速了解什么是計數:
“AND”要求對(x)計數進行吃乘積。 “OR”要求對(+)計數進行疊加。
你可以去查找證據……或者快速閱讀這個例子,滿足自己的求知欲:如果有2種素食套餐和3種肉食套餐可供我選擇,那么一共有多少種選擇呢?答案是2+3=5種可能。假如我確定會選擇一個主餐,要從2份甜品之中選擇一樣,這種情況下會有多少種套餐組合呢?答案是共有5x2=10種。不信嗎?你可以找幾道菜,把所有組合一一寫出來。
隨機組合的套餐是素食的概率是多少?
分子= 2x2=4;;分母=10
答案=4/10=40%
超越事件
現在看了三章,但突然教材中有關組合分析的內容全部消失了。當你入門排列組合的時候,它們就銷聲匿跡了。與此同時,分布變得無處不在。發生了什么?
可以思考如下問題:“你需要至少等待十分鐘才能上公交車的概率是多少?”這會是一個很難“數”出來的問題(到底需要多少秒呢?),計數在這里甚至會變得有些棘手,因為你不能用計數的方式分割時間這個連續的介質。更糟的是,有些公交車司機可能會根據公交車的延遲程度,考慮是否停下來抽煙休息。你怎么能列舉這種情況?不可能做到的。也許計數在這里根本不適用…..
學習基于頻率的概率定義時,將遇到這種說法:“如果上文事件在無限平行宇宙中發生(限定,或者假設這一事件受某些規則制約),有多少公交車會在超過十分鐘以后到?”(平行宇宙?!難怪我們數據猿總是眼光清奇)
然后(通常是很久之后),當到達課本貝葉斯數據的主觀概率定義章節時,你將可能根據你自己的感受建立分布。看見沒有,在你被剝奪列舉事件的能力后,剩下的是不是方法是不是很復雜?不過對于生日問題來說,假設所有366個生日出現的概率相同,我們還可以繼續數數。
什么,你不喜歡我的假設?想開點吧,所有的統計數據都關乎假設——否則宇宙會陷入一片混亂。如果不喜歡我的假設,覺得我的方案不是你期待的,那就提出一套新的方案來。。我們可以隨心所欲提出假設,數據也因此富有創造性。在這里我想不恰當地引用George Box的一句名言:“所有的解決方案都是錯誤的,但一旦某一個方案符合你一直以來的假設,那它就可能對你有用。”
沒有稱贊之意
解決生日問題的最后組件是補數,另一方面它也被稱為NOT。
P(not A)= 1- P(A)
這個公式讀作:“某一事件的概率(由于創造力有限,我們將其稱為事件A)不發生的概率等于100%的概率減去該事件發生的概率。”
所以投擲骰子不出現點6的概率是多少呢?
答案是1-1/6=5/6
好的,這就是所有內容。現在準備解決生日問題了!
生日問題
問題是什么來著?
如果一組有N個人,至少出現兩個人是同一天生日的概率是多少?
那就來搭建“樂高塊”吧…..
生日問題的分母
一個人有多少種生日的可能呢,366種(上文提過)。
所以N=30時會有多少生日數量嗎?
第一個人有366種可能,第二個人也有366種,第三個人也是366種……然后第N個人也是366種情況。把這N個366相乘就是結果了!
分母=366^ N,蒼天好大一個數! N為30,結果就是一個76位數,比1000后面再跟24組“000” 的數還大(給事物命名不好玩嗎?)
生日問題的分子
準備迎接令你暈頭轉向的部分吧。這里需要記錄所有不同的可能,保證至少有兩個人是同一天過生日。所以如果第一個人有366中選項,而第29個人有1個選項,因為需要和第一個人相符,但可能是第二個人或者第十七個人,抑或有三個人的生日在同一天,或者……不,試圖將所有的可能選項記在腦海里會變得很亂。
……這就是為什么生日問題會成為一項很有趣的工程。在看訣竅之前需要絞盡腦汁(或者到網上跪求解題攻略。你是這樣找到這條博文的嗎?很好,我懂你了)。
解決生日問題的竅門
與其列舉所有的兩個以上的人在同一天生日的可能,不如將問題轉化為一個更簡單的切入角度:尋找問題對立面!
P(至少有兩個人是同一天生日)=1-P(所有人都不是同一天生日)
所以我們只需要求以下問題的答案:“沒有任何一個人與另一個人是同一天生日的概率是多少?”也就是說,所有人都不是同一天生日的概率是多少?
“所有人都不是同一天生日”的分母
答案仍然是366^ N。通過對問題的補數進行轉化,我們將重點放到分子上,讓分母保持不變。
“所有人都不是同一天生日”的分子
這就是神奇之處!
第一個人的生日有366種可能(貪婪的家伙)然而第二個人只有365種可能因為我們要求他們的生日不在同一天。如果第一個人的生日在10月8日,我們就把所有在10月8日過生日的人排除在外。這樣每個樣本中的成員的可能生日數量將越來越少。
所以366是第一個人的可能數量,而365是第一個人的可能數量而364是第三個人的可能數量……而(367-N)是第N個人的可能數量。
如果N 是30,將各個數相乘,見證奇跡!
366 x 365 x 364 x 363 x 362 x 361 x 360 x 359 x 358 x 357 x 356 x 355 x 354 x 353 x 352 x 351 x 350 x 349 x 348 x 347 x 346 x 345 x 344 x 343 x 342 x 341 x 340 x 339 x 338 x 337 = …
啊,又是一個76位數的數字。
但是,幸運的是,計算機會幫我們處理除法問題,如果操作得當的話。
也許這不是我們需要的
P(所有39個人的生日都不在同一天)=(366 x 365 x 364 x 363 x 362 x 361 x 360 x 359 x 358 x 357 x 356 x 355 x 354 x 353 x 352 x 351 x 350 x 349 x 348 x 347 x 346 x 345 x 344 x 343 x 342 x 341 x 340 x 339 x 338 x 337) / (366 ^ 30)
=0.3
最后,就是我們需要的數值!
P(30個人有人是同一天生日) = 1-0.3 =70%
在30個人的組中,有人是同一天的生日的概率是~70%。
我希望你沒有賭10美元說,有人的生日在同一天的概率小于每個人的生日都不在同一天的概率……但是如果你真的賭了,我不反對把錢捐給維基百科。
賭錯結果很可能是因為你低估了一組數據不重復的難度——如果你是在門口負責攔截所有與室內的人同一天生日的人的保鏢,不久之后想進入房內的人就會失望。
這取決于你有多少個朋友……
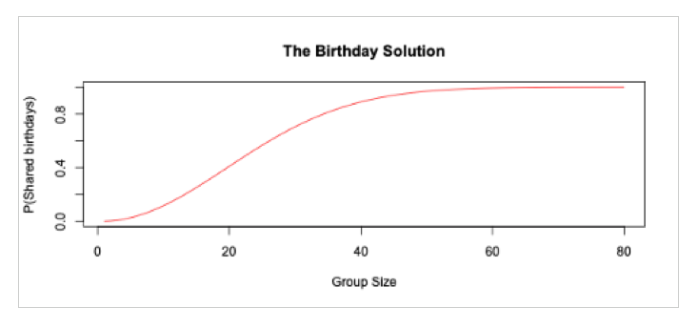
我可以用兩分鐘,通過電腦上的R程序得出每一個N的概率。如果你好奇具體數值是什么(N等于23時概率為50%,N等于55時概率為99%),可以來體驗我編寫的代碼串。可能不太好看,但絕對好用。無需下載,就可以在瀏覽器上運行。
- # Initialize settings for N = 1:
- probability <- 0
- numerator <- 366
- denominator <- 366# Loops are terrible in R, let's make one anyways:
- for (N in 2:80) {
- numerator <- numerator * (366 + 1 - N)
- denominator <- denominator * 366
- p <- 1 - (numerator / denominator)
- probability <- c(probability, p)
- }# Look at the answer to 2 decimal places:
- paste("For N =", 1:80, "prob is", round(probability, 2))# Plot!
- plot(1:80, probability, xlab = "Group Size", ylab = "P(Shared birthdays)", type = "l", col = "red", main = "The Birthday Solution")
我們學到了什么?
除了一些基本概率知識(處理概率問題的不同方法,分子和分母的計算方法),以及計數原則(加法原則和乘法原則)以外,這篇文章的主旨是,為什么需要以特定順序解決特定問題。
為什么在教材開始,計數是重中之重,而在后續內容中,計數會淡出我們的視野,留下憤憤不平的我們?結果貌似說明每一種方法都對應著一種目的,每一種事件發生的概率相等這一前提對于專業人員來說,過于淺顯,無法消化……即使在生日問題上也是如此。當業余人士想象數據分析猿每一天都在干什么的時候,他們首先想到的是數牌和拋硬幣,這不是很好玩嗎?辟謠跑斷腿啊!
生日問題之所以是數據分析入門的經典問題,是因為這個問題上所需的腦力剛剛好:數據分析員需要學習如何轉化問題,以使轉化后的問題更便于解題。采取簡單粗暴的辦法將難以計算,因此需要另辟蹊徑。如果你選擇了數據分析的生活,時刻準備迎接一系列拋擲硬幣和轉化的問題。