在萬(wàn)物相連的世界里，用戶并不是獨(dú)立的個(gè)體，彼此之間都有某種聯(lián)系。構(gòu)建機(jī)器學(xué)習(xí)模型時(shí)，有時(shí)也會(huì)將這種聯(lián)系放入模型中。

[[277932]]

雖然關(guān)系數(shù)據(jù)庫(kù)中無(wú)法在不同數(shù)行(用戶)間使用這種關(guān)系，但在圖數(shù)據(jù)庫(kù)里，這樣做非常簡(jiǎn)單。

本文將介紹一些數(shù)據(jù)科學(xué)家必知的重要的圖算法，并闡釋如何用Python來(lái)使用它們。

另外，強(qiáng)烈推薦先學(xué)習(xí)圖理論基礎(chǔ)。

圣地亞哥大學(xué)發(fā)布于Coursera上的大數(shù)據(jù)課程的圖分析課：https://www.coursera.org/learn/big-data-graph-analytics?ranMID=40328&ranEAID=lVarvwc5BD0&ranSiteID=lVarvwc5BD0-uD3tAFL0mCUdzcfwDd6FTQ&siteID=lVarvwc5BD0-uD3tAFL0mCUdzcfwDd6FTQ&utm_content=2&utm_medium=partners&utm_source=linkshare&utm_campaign=lVarvwc5BD0

1. 連通分支

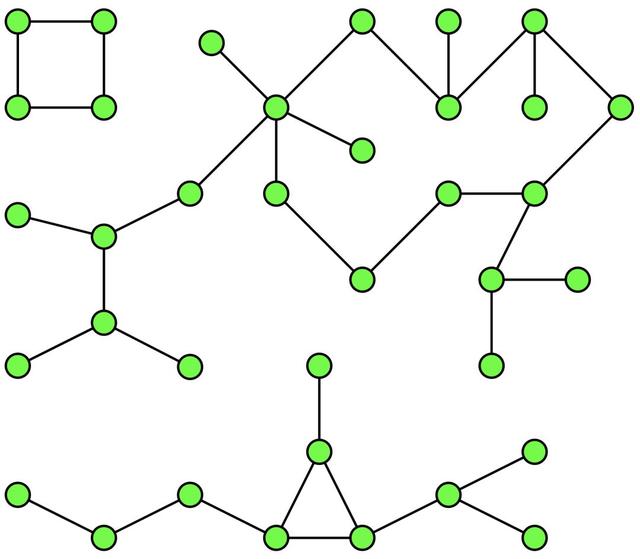
包含3個(gè)連接組件的圖

大家都知道聚類算法如何工作吧?

簡(jiǎn)單地說(shuō)，就是將連通分支看作一種硬聚類算法，讓它在相關(guān)/相連數(shù)據(jù)中找到聚類/島。

舉個(gè)具體的例子：假設(shè)有一份連接世界上任意兩個(gè)城市的道路數(shù)據(jù)，而你需要借此找到世界上所有大洲和所包含的城市。

這要如何實(shí)現(xiàn)呢?開(kāi)動(dòng)腦筋吧。

此處使用的連通分支算法是基于BFS/DFS的特殊情況，此處不多贅述。以下會(huì)解釋如何使用Networkx啟動(dòng)和運(yùn)行代碼。

應(yīng)用

從零售的角度來(lái)看：假設(shè)有很多客戶使用很多的帳戶，連通分支算法可用于在數(shù)據(jù)集中找出不同的家庭。

根據(jù)相同的信用卡使用情況、相同的地址或相同的電話號(hào)碼等，可以假定客戶ID之間的聯(lián)系(路)。一旦有了這些聯(lián)系，就可以對(duì)其運(yùn)行連通分支算法來(lái)創(chuàng)建單獨(dú)的集群，然后為其分配一個(gè)家庭ID。

接著就可以使用這些家庭ID根據(jù)家庭需求提供個(gè)性化推薦。還可以用它來(lái)創(chuàng)建基于家族的分組特性，從而不斷完善分類算法。

從金融角度來(lái)看：這些家庭ID還能用來(lái)捕獲欺詐。如果某個(gè)賬戶有過(guò)欺詐行為，關(guān)聯(lián)賬戶也很可能實(shí)施欺詐。

應(yīng)用的無(wú)限可能性全憑你的想象定奪。

編碼

此處將使用Python中的Networkx模塊來(lái)創(chuàng)建和分析圖表。

先看一個(gè)會(huì)用到的示例圖，其中包含城市和城市之間的距離信息。

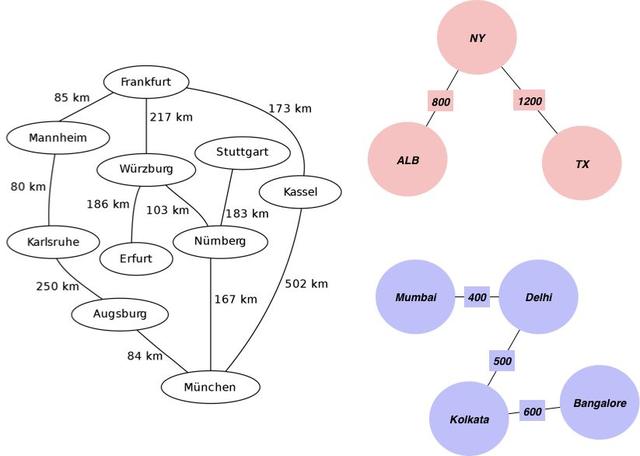
隨機(jī)距離示意圖

首先，創(chuàng)建聯(lián)系列表和作為聯(lián)系權(quán)重的距離列表：

edgelist = [['Mannheim', 'Frankfurt', 85], ['Mannheim', 'Karlsruhe', 80], ['Erfurt', 'Wurzburg', 186], ['Munchen', 'Numberg', 167], ['Munchen', 'Augsburg', 84], ['Munchen', 'Kassel', 502], ['Numberg', 'Stuttgart', 183], ['Numberg', 'Wurzburg', 103], ['Numberg', 'Munchen', 167], ['Stuttgart', 'Numberg', 183], ['Augsburg', 'Munchen', 84], ['Augsburg', 'Karlsruhe', 250], ['Kassel', 'Munchen', 502], ['Kassel', 'Frankfurt', 173], ['Frankfurt', 'Mannheim', 85], ['Frankfurt', 'Wurzburg', 217], ['Frankfurt', 'Kassel', 173], ['Wurzburg', 'Numberg', 103], ['Wurzburg', 'Erfurt', 186], ['Wurzburg', 'Frankfurt', 217], ['Karlsruhe', 'Mannheim', 80], ['Karlsruhe', 'Augsburg', 250],["Mumbai", "Delhi",400],["Delhi", "Kolkata",500],["Kolkata", "Bangalore",600],["TX", "NY",1200],["ALB", "NY",800]] 

用 Networkx創(chuàng)建一個(gè)圖：

g = nx.Graph() 
for edge in edgelist: 
g.add_edge(edge[0],edge[1], weight = edge[2]) 

現(xiàn)在要從這張圖中找出不同的大陸及其城市。

可以這樣/(按如下方式)使用連通分支算法：

for i, x in enumerate(nx.connected_components(g)): 
print("cc"+str(i)+":",x) 
------------------------------------------------------------ 
cc0: {'Frankfurt', 'Kassel', 'Munchen', 'Numberg', 'Erfurt', 'Stuttgart', 'Karlsruhe', 'Wurzburg', 'Mannheim', 'Augsburg'} 
cc1: {'Kolkata', 'Bangalore', 'Mumbai', 'Delhi'} 
cc2: {'ALB', 'NY', 'TX'} 

如上所示，只需要使用聯(lián)系和頂點(diǎn)就可以在數(shù)據(jù)中找到不同的組件。這個(gè)算法可以在不同的數(shù)據(jù)上運(yùn)行來(lái)滿足以上提到的任何案例。

2. 最短路徑

上面已經(jīng)得到德國(guó)城市以及各城市距離的圖。

接著，要得出從法蘭克福(起始節(jié)點(diǎn))到慕尼黑的最短距離。

解決此問(wèn)題的算法叫Dijkstra算法。用Dijkstra本人的話來(lái)說(shuō)：

從鹿特丹到格羅寧根的捷徑是什么?或者說(shuō)，從任意一個(gè)城市到另一個(gè)城市。設(shè)計(jì)這個(gè)最短路徑的算法，我只花了20分鐘。一天早上，我和年輕的未婚妻在阿姆斯特丹購(gòu)物。逛累了之后，我們坐在咖啡館露臺(tái)上喝了一杯咖啡，我就想能不能做到這一點(diǎn)，然后就設(shè)計(jì)了最短路徑算法。就像之前所說(shuō)，這是一個(gè)20分鐘的發(fā)明。事實(shí)上，這本書在三年后的1959年出版，現(xiàn)在還能讀到。它是本很好的書，因?yàn)槲耶?dāng)時(shí)沒(méi)有用鉛筆和紙來(lái)設(shè)計(jì)。后來(lái)我發(fā)現(xiàn)，不用鉛筆和紙?jiān)O(shè)計(jì)的好處之一是，設(shè)計(jì)時(shí)必須要化繁為簡(jiǎn)。最終，我沒(méi)想到，這個(gè)算法竟然成了我的成名作之一。

—— Edsger Dijkstra, 和Philip L. Frana的一段采訪對(duì)話，美國(guó)計(jì)算機(jī)學(xué)會(huì)通訊，2001[3]

應(yīng)用

• Dijkstra算法的演變版本被廣泛應(yīng)用于谷歌地圖中用來(lái)尋找最短路徑。
• 假設(shè)你在沃爾瑪工作，已知不同的通道和所有通道之間的距離，求出A通道到客戶所在的D通道的最短路徑。

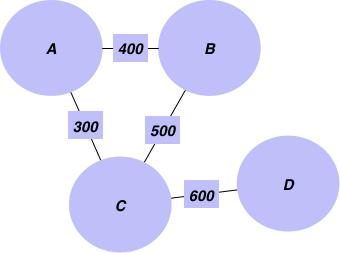
•  領(lǐng)英上有很多一級(jí)聯(lián)系和二級(jí)聯(lián)系。這些聯(lián)系背后都是如何運(yùn)作的呢?

編碼

print(nx.shortest_path(g, 'Stuttgart','Frankfurt',weight='weight')) 
print(nx.shortest_path_length(g, 'Stuttgart','Frankfurt',weight='weight')) 
-------------------------------------------------------- 
['Stuttgart', 'Numberg', 'Wurzburg', 'Frankfurt'] 
503 

還可以使用以下命令找到所有城市對(duì)之間的最短路徑：

for x in nx.all_pairs_dijkstra_path(g,weight='weight'): 
 print(x) 
-------------------------------------------------------- 
('Mannheim', {'Mannheim': ['Mannheim'], 'Frankfurt': ['Mannheim', 'Frankfurt'], 'Karlsruhe': ['Mannheim', 'Karlsruhe'], 'Augsburg': ['Mannheim', 'Karlsruhe', 'Augsburg'], 'Kassel': ['Mannheim', 'Frankfurt', 'Kassel'], 'Wurzburg': ['Mannheim', 'Frankfurt', 'Wurzburg'], 'Munchen': ['Mannheim', 'Karlsruhe', 'Augsburg', 'Munchen'], 'Erfurt': ['Mannheim', 'Frankfurt', 'Wurzburg', 'Erfurt'], 'Numberg': ['Mannheim', 'Frankfurt', 'Wurzburg', 'Numberg'], 'Stuttgart': ['Mannheim', 'Frankfurt', 'Wurzburg', 'Numberg', 'Stuttgart']})('Frankfurt', {'Frankfurt': ['Frankfurt'], 'Mannheim': ['Frankfurt', 'Mannheim'], 'Kassel': ['Frankfurt', 'Kassel'], 'Wurzburg': ['Frankfurt', 'Wurzburg'], 'Karlsruhe': ['Frankfurt', 'Mannheim', 'Karlsruhe'], 'Augsburg': ['Frankfurt', 'Mannheim', 'Karlsruhe', 'Augsburg'], 'Munchen': ['Frankfurt', 'Wurzburg', 'Numberg', 'Munchen'], 'Erfurt': ['Frankfurt', 'Wurzburg', 'Erfurt'], 'Numberg': ['Frankfurt', 'Wurzburg', 'Numberg'], 'Stuttgart': ['Frankfurt', 'Wurzburg', 'Numberg', 'Stuttgart']}).... 

3. 最小生成樹(MST)

現(xiàn)在另一個(gè)問(wèn)題來(lái)了。假設(shè)你在水管鋪設(shè)公司或互聯(lián)網(wǎng)纖維公司工作，需要用最少的電線/管道連接圖中的所有城市，這該怎么做呢?

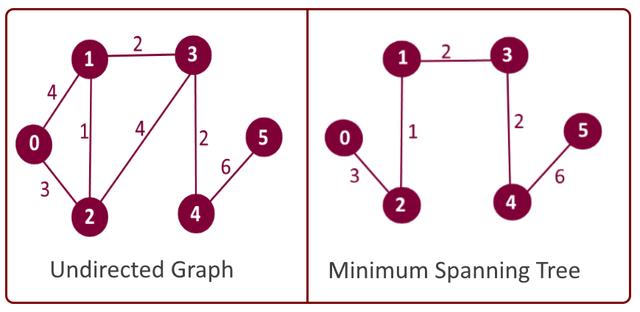
一個(gè)無(wú)向圖，它的MST在右邊

應(yīng)用

• MST被直接應(yīng)用于網(wǎng)絡(luò)設(shè)計(jì)中。其中包括電腦網(wǎng)絡(luò)、電訊網(wǎng)絡(luò)、運(yùn)輸網(wǎng)絡(luò)、供水網(wǎng)絡(luò)和電網(wǎng)(最初設(shè)計(jì)目的)
• MST還用于解決旅行商問(wèn)題
• 聚類——首先建構(gòu)MST，接著用簇間距離和簇內(nèi)距離確定閾值，從而打破MST中的一些聯(lián)系
• 圖像分割——首先在圖中構(gòu)建MST，其中像素是節(jié)點(diǎn)，像素之間的距離基于一些相似性度量(顏色、強(qiáng)度等)

編碼

# nx.minimum_spanning_tree(g) returns a instance of type graph 
nx.draw_networkx(nx.minimum_spanning_tree(g)) 

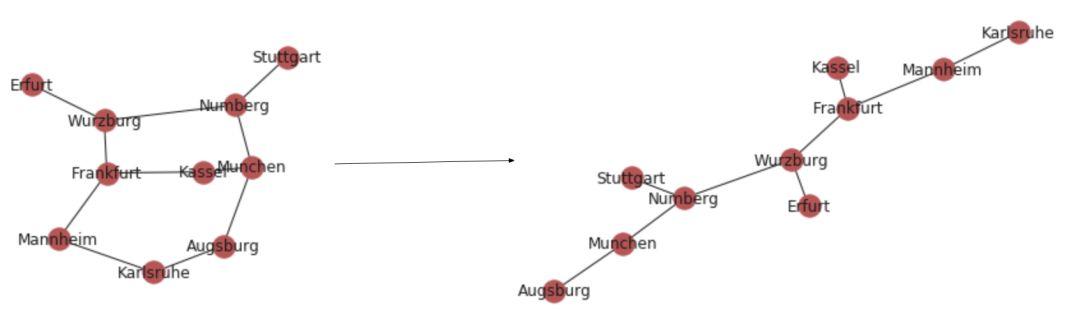
本圖中的MST

如圖所示，上圖中便是要鋪設(shè)的電線。

4. 網(wǎng)頁(yè)排名

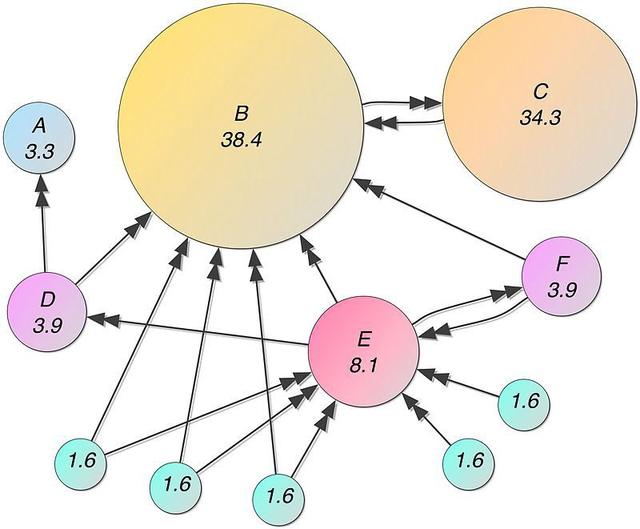
上圖便是谷歌一直以來(lái)的網(wǎng)頁(yè)排名算法。它根據(jù)輸入和輸出連接的數(shù)量和質(zhì)量為頁(yè)面分配分?jǐn)?shù)。

應(yīng)用

網(wǎng)頁(yè)排名可用于需要估算網(wǎng)絡(luò)節(jié)點(diǎn)重要性的任何地方。

• 用于使用引文找到最有影響力的論文
• 在谷歌中用于網(wǎng)頁(yè)排名
• 還可用來(lái)給推特排序——以用戶和推特作為節(jié)點(diǎn)。如果用戶A關(guān)注了用戶B，就創(chuàng)建用戶間的連接。如果用戶發(fā)送或轉(zhuǎn)發(fā)一條推特，則創(chuàng)建用戶和推特之間的連接。
• 推薦引擎

編碼

此練習(xí)會(huì)使用Facebook數(shù)據(jù)。這里有facebook用戶之間的連接/鏈接文件。首先這樣創(chuàng)建Facebook圖形：

# reading the datasetfb = nx.read_edgelist('../input/facebook-combined.txt', create_using = nx.Graph(), nodetype = int) 

它是這樣運(yùn)作的：

pos = nx.spring_layout(fb)import warnings 
warnings.filterwarnings('ignore')plt.style.use('fivethirtyeight') 
plt.rcParams['figure.figsize'] = (20, 15) 
plt.axis('off') 
nx.draw_networkx(fb, pos, with_labels = False, node_size = 35) 
plt.show() 

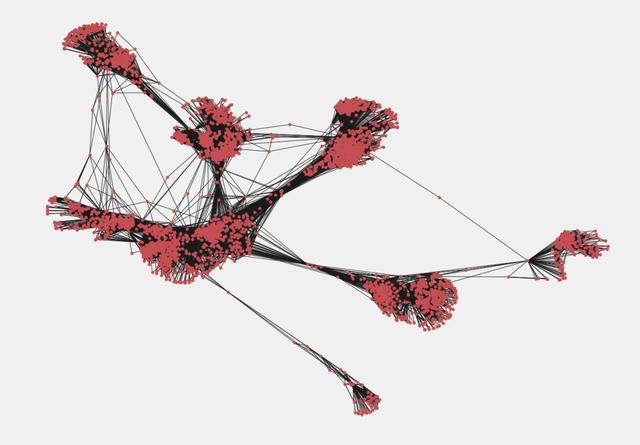
FB用戶圖

現(xiàn)在要找到影響力高的用戶。

直觀地說(shuō)，網(wǎng)頁(yè)排名算法會(huì)給有很多朋友的用戶打高分，而這些用戶又有很多facebook上的朋友。

pageranks = nx.pagerank(fb) 
print(pageranks) 
------------------------------------------------------ 
{0: 0.006289602618466542, 
 1: 0.00023590202311540972, 
 2: 0.00020310565091694562, 
 3: 0.00022552359869430617, 
 4: 0.00023849264701222462, 
........} 

這樣可以得到排序后的網(wǎng)頁(yè)排名算法或最有影響力的用戶：

import operator 
sorted_pagerank = sorted(pagerank.items(), key=operator.itemgetter(1),reverse = True) 
print(sorted_pagerank) 
------------------------------------------------------ 
[(3437, 0.007614586844749603), (107, 0.006936420955866114), (1684, 0.0063671621383068295), (0, 0.006289602618466542), (1912, 0.0038769716008844974), (348, 0.0023480969727805783), (686, 0.0022193592598000193), (3980, 0.002170323579009993), (414, 0.0018002990470702262), (698, 0.0013171153138368807), (483, 0.0012974283300616082), (3830, 0.0011844348977671688), (376, 0.0009014073664792464), (2047, 0.000841029154597401), (56, 0.0008039024292749443), (25, 0.000800412660519768), (828, 0.0007886905420662135), (322, 0.0007867992190291396),......] 

以上ID用于最有影響力的用戶。

這里可以看到很具影響力用戶的子圖：

first_degree_connected_nodes = list(fb.neighbors(3437)) 
second_degree_connected_nodes = [] 
for x in first_degree_connected_nodes: 
 second_degree_connected_nodes+=list(fb.neighbors(x)) 
second_degree_connected_nodes.remove(3437) 
second_degree_connected_nodes = list(set(second_degree_connected_nodes))subgraph_3437 = nx.subgraph(fb,first_degree_connected_nodes+second_degree_connected_nodes)pos = nx.spring_layout(subgraph_3437)node_color = ['yellow' if v == 3437 else 'red' for v in subgraph_3437] 
node_size = [1000 if v == 3437 else 35 for v in subgraph_3437] 
plt.style.use('fivethirtyeight') 
plt.rcParams['figure.figsize'] = (20, 15) 
plt.axis('off')nx.draw_networkx(subgraph_3437, pos, with_labels = False, node_color=node_color,node_size=node_size ) 
plt.show() 

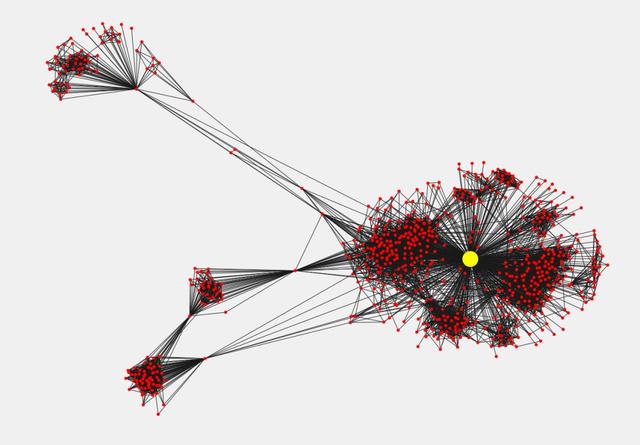
最有影響力的用戶(黃點(diǎn)) 

5.中心性度量

中心度量有很多可以用來(lái)做機(jī)器學(xué)習(xí)模型的特性。以下將介紹其中的兩種。這里可以看到一些其他的測(cè)量方法：https://networkx.github.io/documentation/networkx-1.10/reference/algorithms.centrality.html

中介中心性：朋友最多的用戶很重要，連接兩個(gè)地理位置的用戶也很重要，因?yàn)樗層脩艨梢钥吹絹?lái)自不同地理位置的內(nèi)容。中介中心性量化了一個(gè)特定節(jié)點(diǎn)在其他兩個(gè)節(jié)點(diǎn)之間最短路徑中出現(xiàn)的次數(shù)。

度中心性：即節(jié)點(diǎn)的連接數(shù)。

應(yīng)用

中心性度量可以用作任何機(jī)器學(xué)習(xí)模型的特性。

編碼

以下代碼用于查找子圖的中介中心性。

pos = nx.spring_layout(subgraph_3437) 
betweennessCentrality = nx.betweenness_centrality(subgraph_3437,normalized=True, endpoints=True)node_size = [v * 10000 for v in betweennessCentrality.values()] 
plt.figure(figsize=(20,20)) 
nx.draw_networkx(subgraph_3437, pos=pos, with_labels=False, 
 node_size=node_size ) 
plt.axis('off') 

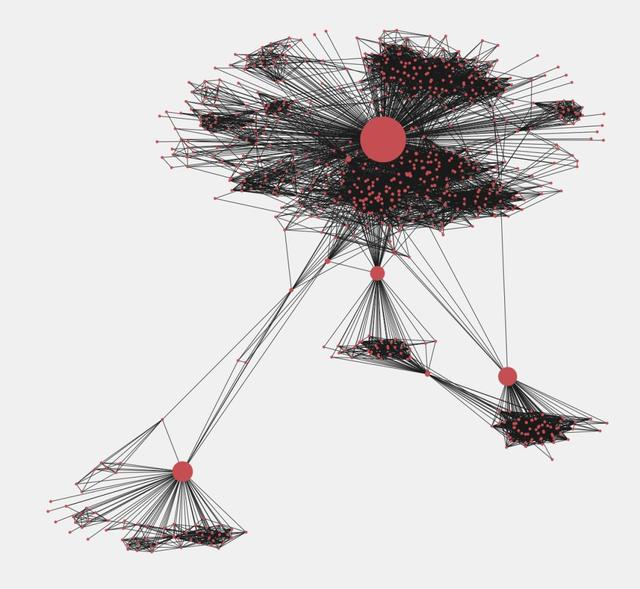
如上可以看到按中介中心性值調(diào)整了節(jié)點(diǎn)的大小。這些節(jié)點(diǎn)可以看作是信息傳遞者。斷開(kāi)高中介中心性的節(jié)點(diǎn)會(huì)將圖分成許多部分。

總結(jié)

本文介紹了一些很具影響力的圖算法，它們從各方面改變了人們的生活方式。

隨著社會(huì)數(shù)據(jù)的大量涌現(xiàn)，網(wǎng)絡(luò)分析可以在很大程度上幫助人們改進(jìn)模型，產(chǎn)生巨大價(jià)值，甚至還會(huì)增進(jìn)人類對(duì)世界的認(rèn)識(shí)。

現(xiàn)今圖算法層出不窮，以上這些是筆者最喜歡的。如果感興趣，歡迎對(duì)這些算法進(jìn)行深入研究。本文僅對(duì)該領(lǐng)域進(jìn)行了一定的介紹。

這里是本文中提到的所有算法的Kaggle Kernel：https://www.kaggle.com/mlwhiz/top-graph-algorithms