在本文中，我將深入探討數(shù)據(jù)科學(xué)中的統(tǒng)計學(xué)習(xí)概念。

首先，我將定義什么是統(tǒng)計學(xué)習(xí)。然后，我們將深入研究統(tǒng)計學(xué)習(xí)中的關(guān)鍵概念。

什么是統(tǒng)計學(xué)習(xí)? 

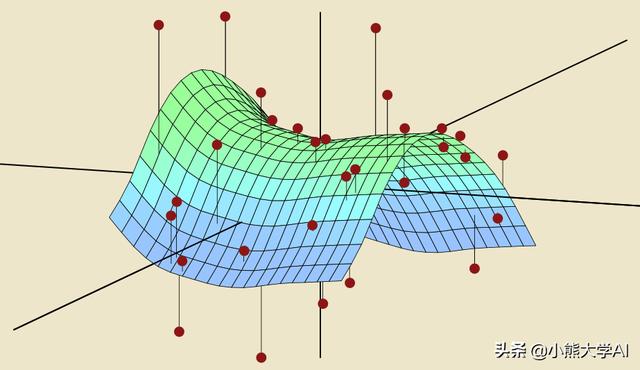
根據(jù)維基百科，統(tǒng)計學(xué)習(xí)理論是從統(tǒng)計學(xué)和功能分析領(lǐng)域中提取的機器學(xué)習(xí)的框架。

機器學(xué)習(xí)是通過軟件應(yīng)用程序?qū)崿F(xiàn)的統(tǒng)計學(xué)習(xí)技術(shù)的表現(xiàn)。

這在實踐中意味著什么?統(tǒng)計學(xué)習(xí)是指能夠使我們更好地理解數(shù)據(jù)的工具和技術(shù)。理解數(shù)據(jù)是什么意思?

在統(tǒng)計學(xué)習(xí)的背景下，有兩種類型的數(shù)據(jù)：

• 可以直接控制的數(shù)據(jù)被稱為自變量。
• 無法直接控制的數(shù)據(jù)被稱為因變量。
• 無法控制的數(shù)據(jù)，即因變量需要預(yù)測或估計。

更好地理解數(shù)據(jù)是根據(jù)自變量來表示因變量。讓我用一個例子來說明它：

• 假設(shè)我想根據(jù)我為電視，廣播和打印分配的廣告預(yù)算來衡量銷售額。我可以控制可以分配給電視，廣播和打印的預(yù)算。我無法控制的是它們將如何影響銷售。我想用我無法控制的數(shù)據(jù)(銷售)作為我可以控制的數(shù)據(jù)(廣告預(yù)算)的函數(shù)。

統(tǒng)計學(xué)習(xí)揭示隱藏的數(shù)據(jù)關(guān)系。依賴數(shù)據(jù)和獨立數(shù)據(jù)之間的關(guān)系。

參數(shù)和模型

運營管理中著名的商業(yè)模式之一是ITO模型。它代表輸入 - 轉(zhuǎn)換 - 輸出模型。這些輸入經(jīng)歷了一些轉(zhuǎn)換創(chuàng)建一個輸出。

統(tǒng)計學(xué)習(xí)也應(yīng)用了類似的概念。有輸入數(shù)據(jù)，輸入數(shù)據(jù)被轉(zhuǎn)換，生成輸出(需要預(yù)測或估計的數(shù)據(jù))。

轉(zhuǎn)換引擎稱為模型。這些是估算輸出的函數(shù)。

這個轉(zhuǎn)換是數(shù)學(xué)上的。將數(shù)學(xué)成分添加到輸入數(shù)據(jù)中以估計輸出。這些成分稱為參數(shù)。

讓我們來看一個例子：

• 是什么決定了一個人的收入?收入是由一個人的教育和多年的經(jīng)驗決定的。估計收入的模型可以是這樣的：收入= c +β0*教育+β1*經(jīng)驗

β0和β1是表示收入與教育和經(jīng)驗相關(guān)的參數(shù)。

教育和經(jīng)驗是可控的變量。這些可控變量具有不同的同義詞。它們被稱為自變量。它們也被稱為特征。

收入是無法控制的變量。它們被稱為目標。

訓(xùn)練和測試 

當我們準備考試時，我們該怎么辦?研究，學(xué)習(xí)，接受，做筆記，練習(xí)，模擬測試。這些是學(xué)習(xí)和準備未知測試的工具。

機器學(xué)習(xí)也使用類似的學(xué)習(xí)概念。數(shù)據(jù)是有限的，可用的數(shù)據(jù)需要謹慎使用。構(gòu)建的模型需要進行驗證。驗證它的方法如下：

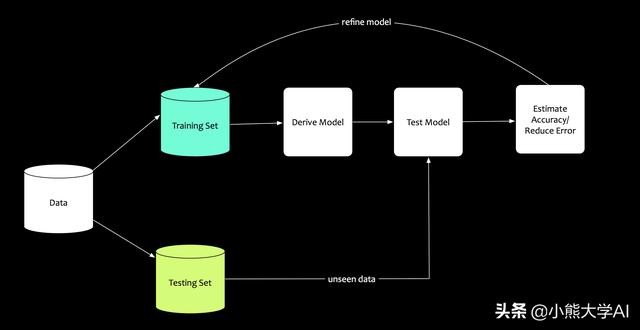
將數(shù)據(jù)拆分為兩部分。

• 一部分進行訓(xùn)練。讓模型從中學(xué)習(xí)，讓模型使用數(shù)據(jù)。此數(shù)據(jù)集稱為訓(xùn)練數(shù)據(jù)。
• 另一部分進行測試。使用未知的數(shù)據(jù)對模型進行“測試”。此數(shù)據(jù)集稱為測試數(shù)據(jù)。

在競爭性考試中，如果準備充分，學(xué)習(xí)合理，那么最后的考試成績也會令人滿意。類似地，在機器學(xué)習(xí)中，如果模型從訓(xùn)練數(shù)據(jù)中很好地學(xué)習(xí)，則它將在測試數(shù)據(jù)上表現(xiàn)良好。

類似地，在機器學(xué)習(xí)中，一旦在測試數(shù)據(jù)集上測試了模型，就會評估模型的性能。它是根據(jù)估計的輸出與實際值的接近程度來評估的。

方差和偏差 

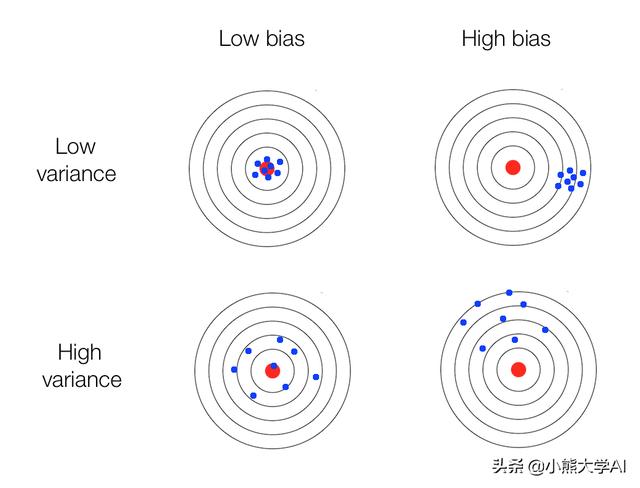
英國著名統(tǒng)計學(xué)家喬治·博克斯曾引用過：

• “All models are wrong, but some are useful。“

沒有一個模型是100%準確的。所有模型都是有誤差的。這些誤差來自兩個來源：

• 偏差
• 方差

讓我試著用類比來解釋這個。

一個7歲的孩子，剛剛學(xué)習(xí)了乘法的概念。他已經(jīng)掌握了1和2的法則。他的下一個挑戰(zhàn)是學(xué)習(xí)3的法則。他非常興奮并開始練習(xí)3的乘法表。他的表是這樣的：

• 3 x 1 = 4
• 3 x 2 = 7
• 3 x 3 = 10
• 3 x 4 = 13
• 3 x 5 = 16

他的同學(xué)和他一樣，但是他的表看起來是這樣的：

• 3 x 1 = 5
• 3 x 2 = 9
• 3 x 3 = 18
• 3 x 4 = 24
• 3 x 5 = 30

讓我們從機器學(xué)習(xí)的角度來研究兩個學(xué)生創(chuàng)建的乘法模型。(我們將兩個孩子認定為A，B)

• A的模型有一個無效的假設(shè)。它假設(shè)乘法運算意味著在結(jié)果之后添加一個1。該假設(shè)引入了偏置誤差。假設(shè)是一致的，即在輸出中加1。這意味著A的模型具有較低的偏差。
• A的模型導(dǎo)致輸出始終與實際相差1個數(shù)。這意味著他的模型具有低方差。
• B的模型輸出沒有邏輯。他的模型輸出與實際值有很大差異。偏差沒有一致的模式。B的模型具有高偏差和高方差。

上面的例子粗略地解釋了方差和偏差的重要概念。

• 偏壓：是模型不考慮數(shù)據(jù)中的所有信息，從而不斷學(xué)習(xí)錯誤的東西的傾向。
• 方差：是模型在不考慮真實信息的情況下獲取隨機信息的傾向。

偏差 - 方差的權(quán)衡 

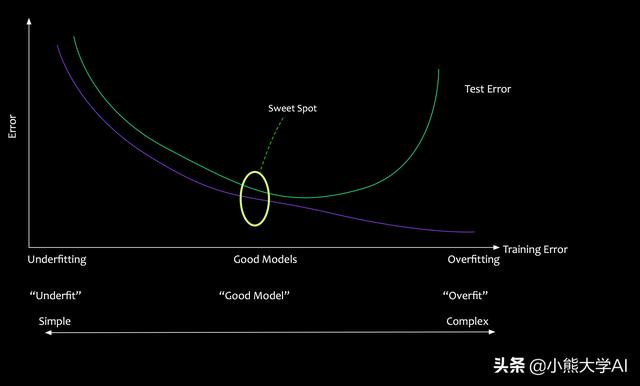
如果模型對特定的數(shù)據(jù)集了解太多，并試圖將相同的模型應(yīng)用于未知的數(shù)據(jù)，則會出現(xiàn)較高的誤差。從給定數(shù)據(jù)集中學(xué)習(xí)太多被稱為過度擬合，它沒有將學(xué)習(xí)推廣到有用的未知數(shù)據(jù)上。另一方面，學(xué)習(xí)太少會導(dǎo)致欠擬合，該模型非常差，甚至無法從給定的數(shù)據(jù)中學(xué)習(xí)。

阿爾伯特愛因斯坦簡潔地總結(jié)了這個概念。他說：

“每件事都應(yīng)該盡可能地簡單，但絕不是越簡單越好。”

在機器學(xué)習(xí)的問題中，一個不斷努力的目標就是找到一個正確的平衡點。創(chuàng)建一個不太復(fù)雜且不太簡單的模型，創(chuàng)建一個通用模型，創(chuàng)建一個相對不準確但有用的模型。

• 過度擬合的模型很復(fù)雜。它在訓(xùn)練數(shù)據(jù)方面表現(xiàn)很好。它在測試數(shù)據(jù)方面表現(xiàn)不佳。
• 欠擬合的模型過于簡單。它對訓(xùn)練數(shù)據(jù)和測試數(shù)據(jù)都無法正常的執(zhí)行。
• 一個好的模型可以平衡欠擬合和過度擬合。它盡可能簡單但并不簡單。

這種平衡行為稱為偏差 - 方差的權(quán)衡。

結(jié)論

統(tǒng)計學(xué)習(xí)是復(fù)雜機器學(xué)習(xí)應(yīng)用的基礎(chǔ)。本文介紹了統(tǒng)計學(xué)習(xí)的一些基本概念。本文的前5個要點是：

1. 統(tǒng)計學(xué)習(xí)揭示隱藏的數(shù)據(jù)關(guān)系。依賴數(shù)據(jù)和獨立數(shù)據(jù)之間的關(guān)系。
2. 模型是轉(zhuǎn)換引擎。參數(shù)是實現(xiàn)轉(zhuǎn)換的要素。
3. 模型使用訓(xùn)練數(shù)據(jù)來學(xué)習(xí)，使用測試數(shù)據(jù)進行評估。
4. All models are wrong, but some are useful(所有模型都是錯誤的; 只有一些是有用的。)
5. 偏差 - 方差權(quán)衡是一種平衡行為。平衡找到最佳平衡點，找到最優(yōu)模型。

我們將在以后繼續(xù)深入研究機器學(xué)習(xí)模型的細節(jié)。