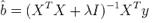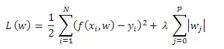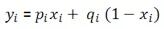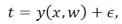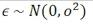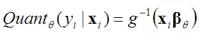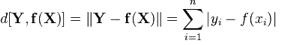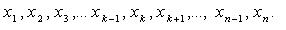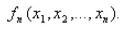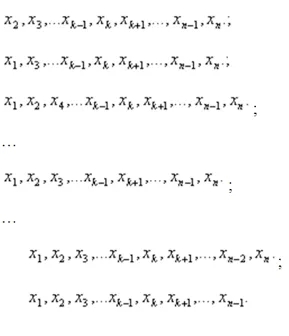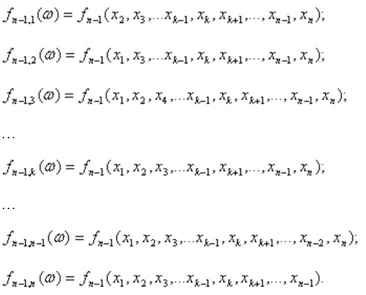除了統計模型和其他的一些算法，回歸是機器學習成功運行的重要構成要素。回歸的核心是尋找變量之間的關系，而機器學習需要根據這種關系來預測結果。

顯然，任何稱職的機器學習工程師都應重視回歸，但回歸也有很多種。線性回歸和邏輯回歸通常是人們最先學習的算法，然而還有許多回歸類型。每種類型都有各自的重要性，并且有最適合應用的情境。那么，該用哪一種呢?

本文將用通俗易懂的方式介紹最常用的回歸類型，遇到具體任務時你便知曉該使用哪一種。

[[267540]]

1. 線性回歸Linear regression

線性回歸是最典型的回歸類型，大約250年前就已出現，也被稱為普通最小二乘法(OLS)和線性最小二乘法回歸。可以使用它對小數據集進行計算，甚至可以手動計算。目前線性回歸常用于插值，但不適合實際預測和主動分析。

另外，現代數據常常結構混亂，線性回歸容易“滯后”：線性回歸過于精確。如果模型對一組數據計算精確，對另一組數據卻極不精確，而線性回歸本應描述一般模式，過于精確會使其在幾乎所有情況下變得不穩定。

2. 嶺回歸Ridge regression

嶺回歸是線性回歸的重要改進，增加了誤差容忍度，對回歸系數進行了限制，從而得到更加真實的結果，并且結果更容易解釋。該方法用于解決自變量之間相互關聯(多重共線性)時的數據冗余問題。

嶺回歸需要使用如下公式來評估參數：

3. 套索回歸Lasso-regression

套索回歸與嶺回歸類似，但回歸系數可為0(模型中排除了一些符號)。

4. 偏最小二乘法回歸Partial least squares(PLS)

與自變量數目相比，觀察結果很少時，或者自變量高度相關時，PLS會很有用。PLS可將自變量減少，并使其不相關，類似于主成分分析。然后，對這些自變量而非原始數據進行線性回歸。

PLS強調發展預測模型，不用于篩選變量。與OLS不同，PLS可以包含多個連續因變量。PLS利用相關結構識別較小的效應，并對因變量中的多元模式進行建模。

[[267543]]

來源：Pexels

5. 邏輯回歸Logistic regression

邏輯回歸廣泛應用于臨床試驗、量化，或者欺詐分析——當測試藥物或信用卡交易的信息可以二進制形式(是/否)獲得時。線性回歸固有的缺點它也有，如低誤差容忍度、依賴數據集，但總的來說，邏輯回歸更好，并且可以簡化為線性回歸類型來簡化計算。有些版本如泊松回歸得到了改進，以便有時需要得到非二進制答案，例如分類、年齡組、甚至回歸樹。

6. 生態回歸 Ecological Regression

生態回歸用于將數據劃分為相當大的層或組的情況(回歸分別應用于每個層或組)，例如，在政治學中生態回歸用于根據匯總數據評估選民的群體行為。

然而，應該警惕“大數據的詛咒”：如果對數百萬次回歸進行統計，其中一些模型可能完全不準確，成功的模型將被高度(且人為)一致的嘈雜模型“擊潰”。因此，這種類型的回歸不適合預測極端事件(地震)和研究因果關系(全球變暖)。

7. 貝葉斯線性回歸Bayesian linear regression

貝葉斯線性回歸與嶺回歸類似，但它的前提是所有可能的誤差都服從正態分布。因此，假設對數據結構有基本了解，就可能獲得更精確的模型(特別是與線性回歸相比)。

然而，在實際操作中，若處理大數據，對數據的初始了解并不能保證準確性，所以這種假設是基于共軛值的，即本質上是人為的，這是這種回歸類型的一個顯著缺陷。

觀測變量的計算：

誤差服從正態分布：

8. 分位數回歸Quantile regression

分位數回歸用于極端事件，包括故意在結果中引入偏差，從而提高模型的準確性。

9. 最小絕對偏差Least absolute deviations(LAD)

最小絕對偏差也稱為最小絕對誤差(LAE)、最小絕對值(LAV)、最小絕對殘差(LAR)、絕對偏差之和或L1范數條件，是最小的模量方法。它用于從包含隨機誤差的測量值中評估未知值，以及估算給定函數的表示法(近似值)。最小絕對偏差看起來像線性回歸，但使用的是絕對值而不是平方。因此，模型的準確性有所提高，且沒有使計算復雜化。

10. 刀切法重采樣Jackknife resampling(大折刀法)

刀切法重采樣是一種用于聚類和數據細化的新型回歸方法。這種方法不具有典型回歸類型的缺點，能為回歸問題提供近似但非常準確、抗誤差的解決方案，自變量相關或不“服從”正態分布時都可使用。

這種類型的回歸很適合黑盒類型預測算法，它非常接近線性回歸，沒有精度損失，即使傳統回歸假設(變量不相關、數據正態分布、條件方差恒定)由于數據性質不被接受，它依舊可以使用。

假設樣本如下：

在概率統計理論中，假設這是一組獨立同分布的隨機變量，且以下是要研究的數據：

約翰•圖基(John Tukey)在1949年提出的觀點(即“大折刀法”)是對一個樣本做大量的研究，排除一個觀察結果(并返回之前被排除的結果)。下面列出了從原始數據中獲得的樣本：

每一項都有n個新樣本，樣本容量為n-1，且都可用來計算計量經濟學感興趣的統計數據的價值(樣本容量減1)：

通過獲得的統計值，可了解其分布和分布的特征，如期望、中值、分位數、散點和均方差。

那么，該使用哪一種回歸?

[[267552]]

• 如果模型需要連續的因變量：線性回歸是最常見和最直接的使用類型。如果有一個連續的因變量，可能要首先考慮線性回歸模型。然而，要注意線性回歸的幾個缺點，如對異常值和多重共線性很敏感。在這種情況下，最好使用更高級的線性回歸變體，如嶺回歸、套索回歸和偏最小二乘法回歸(PLS)。
• 如果模型需要分類因變量：應使用邏輯回歸。這種模型最適合二元因變量。在進行更復雜的分類建模之前，最好先使用這種模型。分類變量的有些值可以根據特征放入可計數的不同組中。邏輯回歸對因變量進行變換，然后使用最大似然估計法而非最小二乘法來估計參數。
• 如果模型需要計數因變量：應使用泊松回歸。計數數據往往遵循泊松分布，因此泊松回歸很適合。使用泊松變量可以計算和評估發生率。