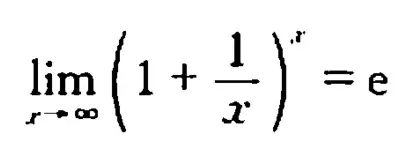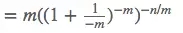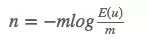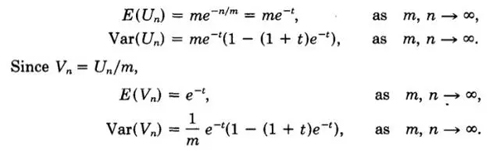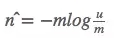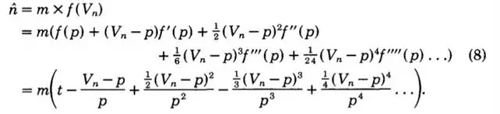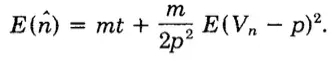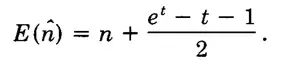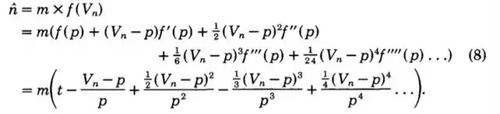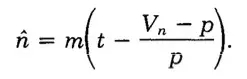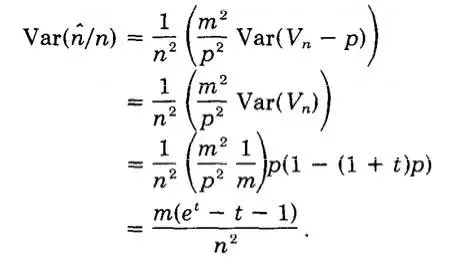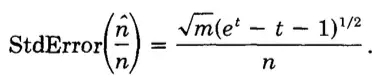大數據計數原理1+0=1這你都不會算(七)
今天的干貨,不是一般的干,噎死人那種干。沒下面這些準備的話直接退出吧,回去度娘啊谷哥啊弄懂是什么東西再回來。
知識儲備必須有這些:
BitMap知識。概率論二項分布。泰勒展開。函數求極限。求期望值。求方差、標準差。log對數變換。極大似然估計。
照例甩一波鏈接。
來了喔。
真的來了喔。
我們先定義幾個代數。
整個BitMap 有m個坑,還要有u個坑還沒被占。我們已經假設了值經過 Hash 后近似服從獨立均勻分布。
對事件進行定義:
A = “經過n個元素進行Hash后,第j個桶值為0”
則A出現的概率如上。意思就是坑為1的概率都是1/m,那么坑為0的概率為 (1 - 1/m),如此重復n次 ,就得到上面的式子了。
又因為每個桶都是獨立的,所以整個BitMap的期望值為A的概率直接乘以m。
做一個小小的trick(小把戲)變換,也就是強行把內部滿足某個求極限的式子。喏,這個。
當m和n都趨向于無窮大的時候,求一下極限,就得到了這個
這個是有u個坑的估計,而我們想知道的是基數n,做一下log變換。
根據極大似然估計的判定定理。
好了,剛剛我們已經得到期望,現在我們求一下方差和比率t的方差和期望,后面有用,至于怎么求的,自行找一下怎么求。
取前三項。原論文里說,因為第二項展開的期望為0,所以保留前三項,求期望得到
代入前面求到的期望值,化簡可以得到。
所以直接除于n,可以得到偏差比率為:
至此,偏差比率的推導就完成啦,能看到這里的都是大神,說實話。
那標準差又是怎么樣的呢?
還是它,泰勒展開。
這里啟發性地取前兩項。
一步一步推導下來,再配合前面求的方差,嗯相信你可以的。
所以標準差就是這樣。
至此,原理,偏差率,標準差都推導完畢,但是還有一點點問題。就是,這樣去算有什么條件呢,對于m的取值?啟發性地取泰勒展開前三項和前兩項又分別代表什么?這個大家自己去論文看,我要是開心,我可能也會說說看。
是不是很干貨?我也知道很干,但是真的要細細閱讀,讀完***搭配上原始論文好好看一下,我看了蠻久的說實話。
好了睡覺了。要是覺得很干就點個贊吧,讓我知道還有人在看。
【本文為51CTO專欄作者“大蕉”的原創稿件,轉載請通過作者微信公眾號“一名叫大蕉的程序員”獲取授權】