[[205570]]

我們展示了深度線性網絡(使用浮點運算實現)實際上并不是線性的，它可以執行非線性計算。我們利用這一點使用進化策略在線性網絡中尋找參數，使我們能夠解決重要問題。

神經網絡通常由一個線性層和非線性函數(比如 tanh 和修正線性單元 ReLU)堆棧而成。如果沒有非線性，理論上一連串的線性層和單一的線性層在數學上是等價的。因此浮點運算是非線性的，并足以訓練深度網絡。這很令人驚訝。

背景

計算機使用的數字并不是***的數學對象，而是使用有限個比特的近似表示。浮點數通常被計算機用于表示數學對象。每一個浮點數由小數和指數的組合構成。在 IEEE 的 float32 標準中，小數分配了 23 個比特，指數分配了 8 個比特，還有一個比特是表示正負的符號位 sign。

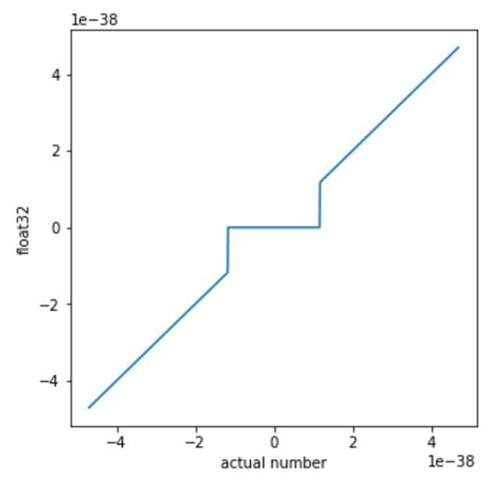
按照這種慣例和二進制格式，以二進制表示的最小非零正常數是 1.0..0 x 2^-126，以下用 min 來指代。而下一個可表示的數是 1.0..01 x 2^-126，可以寫作 min+0.0..01 x 2^-126。很顯然，***和第二個數之間的 gap 比 0 和 min 之間的 gap 小了 2^20 倍。在 float32 標準中，當一個數比最小的可表示數還小的時候，則該數字將被映射為零。因此，近鄰零的所有包含浮點數的計算都將是非線性的。(而反常數是例外，它們在一些計算硬件上可能不可用。在我們的案例中通過設置歸零(flush to zero，FTZ)解決這個問題，即將所有的反常數當成零。)

因此，雖然通常情況下，所有的數字和其浮點數表示之間的區別很小，但是在零附近會出現很大的 gap，而這個近似誤差可能帶來很大影響。

這會導致一些奇怪的影響，一些常用的數學規則無法發揮作用。比如，(a + b) x c 不等于 a x c + b x c。

比如，如果你設置 a = 0.4 x min，b = 0.5 x min，c = 1 / min。

則：(a+b) x c = (0.4 x min + 0.5 x min) x 1 / min = (0 + 0) x 1 / min = 0。

然而：(a x c) + (b x c) = 0.4 x min / min + 0.5 x min x 1 / min = 0.9。

再比如，我們可以設置 a = 2.5 x min，b = -1.6 x min，c = 1 x min。

則：(a+b) + c = (0) + 1 x min = min

然而：(b+c) + a = (0 x min) + 2.5 x min = 2.5 x min。

在這種小尺度的情況下，基礎的加法運算變成非線性的了!

使用進化策略利用非線性

我們想知道這種內在非線性是否可以作為計算非線性的方法，如果可以，則深度線性網絡能夠執行非線性運算。挑戰在于現代微分庫在非線性尺度較小時會忽略它們。因此，使用反向傳播利用非線性訓練神經網絡很困難或不可能。

我們可以使用進化策略(ES)，無需依賴符號微分(symbolic differentiation)法就可以評估梯度。使用進化策略，我們可以將 float32 的零點鄰域(near-zero)行為作為計算非線性的方法。深度線性網絡通過反向傳播在 MNIST 數據集上訓練時，可獲取 94% 的訓練準確率和 92% 的測試準確率(機器之心使用三層全連接網絡可獲得 98.51% 的測試準確率)。相對而言，相同的線性網絡使用進化策略訓練可獲取大于 99% 的訓練準確率、96.7% 的測試準確率，確保激活值足夠小而分布在 float32 的非線性區間內。訓練性能的提升原因在于在 float32 表征中使用非線性的進化策略。這些強大的非線性允許任意層生成新的特征，這些特征是低級別特征的非線性組合。以下是網絡結構：

x = tf . placeholder ( dtype = tf . float32 , shape =[ batch_size , 784 ]) 
 
y = tf . placeholder ( dtype = tf . float32 , shape =[ batch_size , 10 ]) 
 
w1 = tf . Variable ( np . random . normal ( scale = np . sqrt ( 2. / 784 ), size =[ 784 , 512 ]). astype ( np . float32 )) 
 
b1 = tf . Variable ( np . zeros ( 512 , dtype = np . float32 )) 
 
w2 = tf . Variable ( np . random . normal ( scale = np . sqrt ( 2. / 512 ), size =[ 512 , 512 ]). astype ( np . float32 )) 
 
b2 = tf . Variable ( np . zeros ( 512 , dtype = np . float32 )) 
 
w3 = tf . Variable ( np . random . normal ( scale = np . sqrt ( 2. / 512 ), size =[ 512 , 10 ]). astype ( np . float32 )) 
 
b3 = tf . Variable ( np . zeros ( 10 , dtype = np . float32 )) 
 
params = [ w1 , b1 , w2 , b2 , w3 , b3 ] 
 
nr_params = sum ([ np . prod ( p . get_shape (). as_list ()) for p in params ]) 
 
scaling = 2 ** 125 
 
def get_logits ( par ): 
 
h1 = tf . nn . bias_add ( tf . matmul ( x , par [ 0 ]), par [ 1 ]) / scaling 
 
h2 = tf . nn . bias_add ( tf . matmul ( h1 , par [ 2 ]) , par [ 3 ] / scaling ) 
 
o = tf . nn . bias_add ( tf . matmul ( h2 , par [ 4 ]), par [ 5 ]/ scaling )* scaling 
 
return o 

在上面的代碼中，我們可以看出該網絡一共 4 層，***層為 784(28*28)個輸入神經元，這個數量必須和 MNIST 數據集中單張圖片所包含像素點數相同。第二層與第三層都為隱藏層且每層有 512 個神經元，***一層為輸出的 10 個分類類別。其中每兩層之間的全連接權重為服從正態分布的隨機初始化值。nr_params 為加和所有參數的累乘。下面定義一個 get_logist() 函數，該函數的輸入變量 par 應該可以是上面定義的 nr_params，因為定義添加偏置項的索引為 1、3、5，這個正好和前面定義的 nr_params 相符，但 OpenAI并沒有給出該函數的調用過程。該函數***個表達式計算***層和第二層之間的前向傳播結果，即計算輸入 x 與 w1 之間的乘積再加上縮放后的偏置項(前面 b1、b2、b3 都定義為零向量)。后面兩步的計算也基本相似，***返回的 o 應該是圖片識別的類別。不過 OpenAI 只給出了網絡架構，而并沒有給出優化方法和損失函數等內容。