有時候在學習神經網絡教程時，我們通常會看到有的實驗似乎理所當然地就選定了某種神經網絡架構以及特定的網絡層數、激活函數、損失函數等等，卻沒有解釋原因。因為解釋起來有點難。是的，深度學習社區選擇 ReLU(或更現代的選擇 ELU 或 SELU)作為激活函數是「常態」，而且我們基本上也欣然接受，但我們通常并沒有思考這是否是正確的。比如在網絡的層數和優化器的學習率選擇上，我們通常都遵循標準。近日，機器學習開發者兼饒舌歌手 Alex Honchar 在 Medium 上發文分享了自動化這些選擇過程的方式。另外，本文涉及的相關代碼也已在 GitHub 上公開。

代碼地址：https://github.com/Rachnog/Deep-Trading/tree/master/hyperparameters

超參數搜索

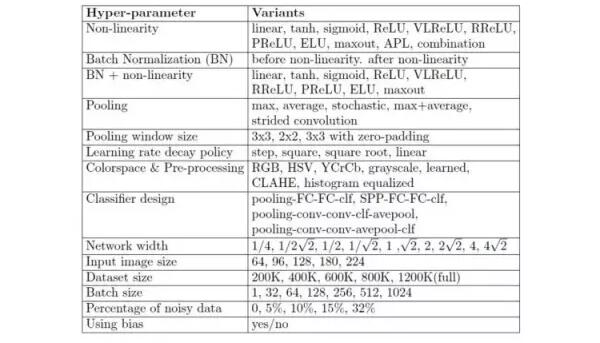
卷積神經網絡訓練的典型超參數的列表

在開始訓練一個模型之前，每個機器學習案例都要選擇大量參數;而在使用深度學習時，參數的數量還會指數式增長。在上面的圖中，你可以看到在訓練計算機視覺卷積神經網絡時你要選擇的典型參數。

但有一個可以自動化這個選擇過程的方法!非常簡單，當你要選擇一些參數和它們的值時，你可以：

• 啟動網格搜索，嘗試檢查每種可能的參數組合，當有一種組合優化了你的標準時(比如損失函數達到最小值)，就停止搜索。
• 當然，在大多數情況下，你可等不了那么久，所以隨機搜索是個好選擇。這種方法可以隨機檢查超參數空間，但速度更快而且大多時候也更好。
• 貝葉斯優化——我們為超參數分布設置一個先決條件，然后在觀察不同實驗的同時逐步更新它，這讓我們可以更好地擬合超參數空間，從而更好地找到最小值。

在這篇文章中，我們將把***一個選項看作是一個黑箱，并且重點關注實際實現和結果分析。

HFT 比特幣預測

我使用的數據來自 Kaggle，這是用戶 @Zielak 貼出的比特幣過去 5 年的每分鐘價格數據，數據集地址：

https://www.kaggle.com/mczielinski/bitcoin-historical-data。

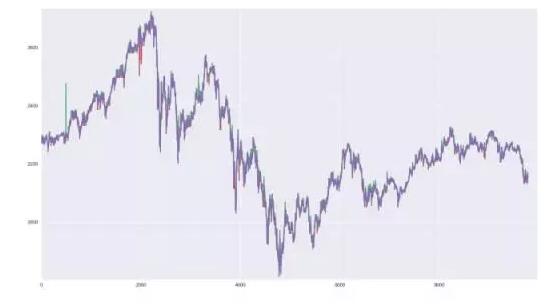
比特幣價格的樣本圖

我們將取出其中最近 10000 分鐘的一個子集，并嘗試構建一個能夠基于我們選擇的一段歷史數據預測未來 10 分鐘價格變化的***模型。

對于輸入，我想使用 OHLCV 元組外加波動，并將這個數組展開以將其輸入多層感知器(MLP)模型。

o = openp[i:i+window] 
h = highp[i:i+window] 
l = lowp[i:i+window] 
c = closep[i:i+window] 
v = volumep[i:i+window] 
volat = volatility[i:i+window] 
x_i = np.column_stack((o, h, l, c, v, volat)) 
x_ix_i = x_i.flatten() 
y_i = (closep[i+window+FORECAST] - closep[i+window]) / closep[i+window] 

優化 MLP 參數

我們將使用 Hyperopt 庫來做超參數優化，它帶有隨機搜索和 Tree of Parzen Estimators(貝葉斯優化的一個變體)的簡單接口。Hyperopt 庫地址：http://hyperopt.github.io/hyperopt

我們只需要定義超參數空間(詞典中的關鍵詞)和它們的選項集(值)。你可以定義離散的值選項(用于激活函數)或在某個范圍內均勻采樣(用于學習率)。

space = {'window': hp.choice('window',[30, 60, 120, 180]), 
        'units1': hp.choice('units1', [64, 512]), 
        'units2': hp.choice('units2', [64, 512]), 
        'units3': hp.choice('units3', [64, 512]), 
        'lr': hp.choice('lr',[0.01, 0.001, 0.0001]), 
        'activation': hp.choice('activation',['relu', 
                                                'sigmoid', 
                                                'tanh', 
                                                'linear']), 
        'loss': hp.choice('loss', [losses.logcosh, 
                                    losses.mse, 
                                    losses.mae, 
                                    losses.mape])} 

在我們的案例中，我想檢查：

• 我們需要更復雜還是更簡單的架構(神經元的數量)
• 激活函數(看看 ReLU 是不是真的是***選擇)
• 學習率
• 優化標準(也許我們可以最小化 logcosh 或 MAE，而不是 MSE)
• 我們需要的穿過網絡的時間窗口，以便預測接下來 10 分鐘

當我們用 params 詞典的對應值替換了層或數據準備或訓練過程的真正參數后(我建議你閱讀 GitHub 上的完整代碼)：

main_input = Input(shape=(len(X_train[0]), ), name='main_input') 
x = Dense(params['units1'], activation=params['activation'])(main_input) 
x = Dense(params['units2'], activation=params['activation'])(x) 
x = Dense(params['units3'], activation=params['activation'])(x) 
output = Dense(1, activation = "linear", name = "out")(x) 
final_model = Model(inputs=[main_input], outputs=[output]) 
opt = Adam(lr=params['lr']) 
final_model.compile(optoptimizer=opt,  loss=params['loss']) 
history = final_model.fit(X_train, Y_train,  
                  epochs = 5,  
                  batch_size = 256,  
                  verbose=0,  
                  validation_data=(X_test, Y_test), 
                  shuffle=True) 
pred = final_model.predict(X_test) 
predpredicted = pred 
original = Y_test 
mse = np.mean(np.square(predicted - original)) 
sys.stdout.flush()  
return {'loss': -mse, 'status': STATUS_OK} 

我們將檢查網絡訓練的前 5 epoch 的性能。在運行了這個代碼之后，我們將等待使用不同參數的 50 次迭代(實驗)執行完成，Hyperopt 將為我們選出其中***的選擇，也就是：

best:  
{'units1': 1, 'loss': 1, 'units3': 0, 'units2': 0, 'activation': 1, 'window': 0, 'lr': 0} 

這表示我們需要***兩層有 64 個神經元而***層有 512 個神經元、使用 sigmoid 激活函數(有意思)、取經典的學習率 0.001、取 30 分鐘的時間窗口來預測接下來的 10 分鐘……很好。

結果

首先我們要構建一個「金字塔」模式的網絡，我常常用這種模式來處理新數據。大多時候我也使用 ReLU 作為激活函數，并且為 Adam 優化器取標準的學習率 0.002.

X_train, X_test, Y_train, Y_test = prepare_data(60) 
main_input = Input(shape=(len(X_train[0]), ), name='main_input') 
x = Dense(512, activation='relu')(main_input) 
x = Dense(128, activation='relu')(x) 
x = Dense(64, activation='relu')(x) 
output = Dense(1, activation = "linear", name = "out")(x) 
final_model = Model(inputs=[main_input], outputs=[output]) 
opt = Adam(lr=0.002) 
final_model.compile(optoptimizer=opt,  loss=losses.mse) 

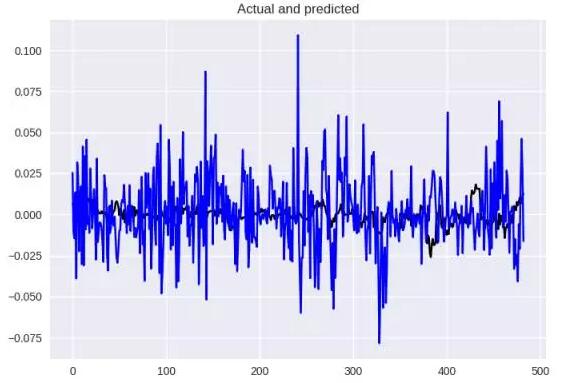
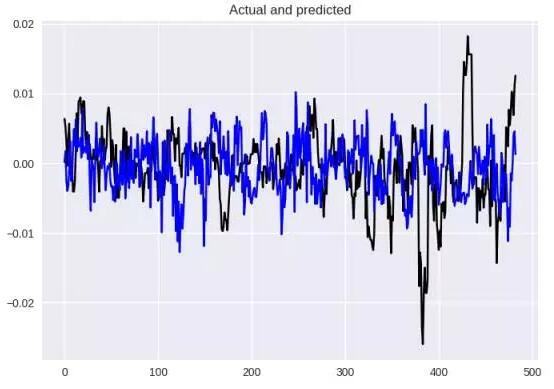
看看表現如何，藍色是我們的預測，而黑色是原始情況，差異很大，MSE = 0.0005，MAE = 0.017。

基本架構的結果

現在看看使用 Hyperopt 找到的超參數的模型在這些數據上表現如何：

X_train, X_test, Y_train, Y_test = prepare_data(30) 
main_input = Input(shape=(len(X_train[0]), ), name='main_input') 
x = Dense(512, activation='sigmoid')(main_input) 
x = Dense(64, activation='sigmoid')(x) 
x = Dense(64, activation='sigmoid')(x) 
output = Dense(1, activation = "linear", name = "out")(x) 
final_model = Model(inputs=[main_input], outputs=[output]) 
opt = Adam(lr=0.001) 
final_model.compile(optoptimizer=opt, loss=losses.mse) 

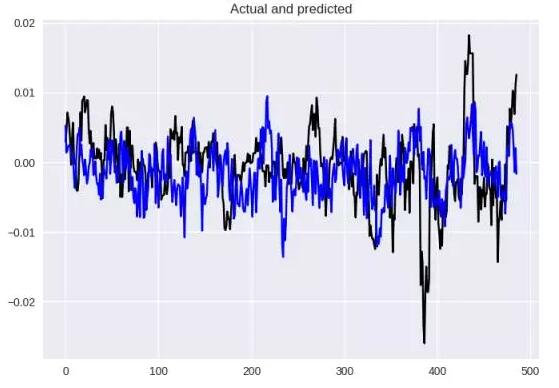
使用 Hyperopt 找的參數所得到的結果

在這個案例中，數值結果(MSE = 4.41154599032e-05，MAE = 0.00507)和視覺效果都好得多。

老實說，我認為這不是個好選擇，尤其是我并不同意如此之短的訓練時間窗口。我仍然想嘗試 60 分鐘，而且我認為對于回歸而言，Log-Cosh 損失是更加有趣的損失函數選擇。但我現在還是繼續使用 sigmoid 激活函數，因為看起來這就是表現極大提升的關鍵。

X_train, X_test, Y_train, Y_test = prepare_data(60) 
main_input = Input(shape=(len(X_train[0]), ), name='main_input') 
x = Dense(512, activation='sigmoid')(main_input) 
x = Dense(64, activation='sigmoid')(x) 
x = Dense(64, activation='sigmoid')(x) 
output = Dense(1, activation = "linear", name = "out")(x) 
final_model = Model(inputs=[main_input], outputs=[output]) 
opt = Adam(lr=0.001) 
final_model.compile(optoptimizer=opt,  loss=losses.logcosh) 

這里得到 MSE = 4.38998280095e-05 且 MAE = 0.00503，僅比用 Hyperbot 的結果好一點點，但視覺效果差多了(完全搞錯了趨勢)。

結論

我強烈推薦你為你訓練的每個模型使用超參數搜索，不管你操作的是什么數據。有時候它會得到意料之外的結果，比如這里的超參數(還用 sigmoid?都 2017 年了啊?)和窗口大小(我沒料到半小時的歷史信息比一個小時還好)。

如果你繼續深入研究一下 Hyperopt，你會看到你也可以搜索隱藏層的數量、是否使用多任務學習和損失函數的系數。基本上來說，你只需要取你的數據的一個子集，思考你想調節的超參數，然后等你的計算機工作一段時間就可以了。這是自動化機器學習的***步!

原文：

https://medium.com/@alexrachnog/neural-networks-for-algorithmic-trading-hyperparameters-optimization-cb2b4a29b8ee

【本文是51CTO專欄機構“機器之心”的原創譯文，微信公眾號“機器之心( id: almosthuman2014)”】

戳這里，看該作者更多好文