[[198700]]

1. 引言

經典物理學的主角是物質和能量。20 世紀初，愛因斯坦寫下E =mc2 ，將質量和能量統一在了一起。而從那之后，一個新角色——信息(Information)——逐漸走向了物理學舞臺的中央。信息是關于不確定程度的度量。Shannon 創立信息論的初衷是為了定量化地描述信息的存儲和傳輸。Jaynes 從信息論的角度研究多粒子體系，重新闡釋了統計力學。原來，物理學家所熟知的熱力學熵與Shannon 用來衡量信息量的信息熵(Information Entropy)系出同源。Landauer 指出擦除信息會增加熱力學熵，從而產生熱量。因此，對于信息的一切處理(比如計算)都受到熱力學基本定律的約束。這些工作使人們逐漸意識到，信息不是一個單純的數學概念，而是與物質和能量一樣基本的物理概念。

量子力學給物理世界帶來了固有的不確定性，從而促生了量子信息理論。量子信息論中最核心的概念是量子糾纏。如果兩個微觀粒子的整體波函數不能夠被寫成各部分的直積，那么它們之間就存在糾纏。對于存在量子糾纏的體系，觀察其中的一部分能夠告訴我們關于另外一部分的信息。類比于經典信息熵， 我們使用糾纏熵(Entanglement Entropy)來度量量子糾纏的大小。量子信息論的視角，特別是量子糾纏的概念在現代物理學的研究中扮演著日趨重要的角色。

凝聚態物理學家用量子糾纏來刻畫量子物質態。傳統上，他們使用對稱性和宏觀序參量來區分不同的物質狀態。這成功地解釋了超流體、超導體、磁性等豐富多彩的自然現象。然而，近些年來人們發現了越來越多僅用對稱性難以區分的物質態，比如不同種類的自旋液體態、分數量子霍爾態等等。量子糾纏可以給這些新的物質態一個恰當的標記。比如，糾纏熵隨著體系尺寸的標度行為反映了量子物質態的基本特性。而對于標度行為的修正也可能包含著關于物質態的普適信息。研究量子物質態中糾纏的大小和模式成為現代凝聚態物理的一個核心問題。此外，量子糾纏還指引計算物理學家發展高效的數值算法精確地模擬量子多體現象。本次專題的另外幾篇文章介紹了使用張量網絡態(Tensor Network State)方法研究量子多體問題的進展。張量網絡算法的成功很大程度上來源于量子物質態典型的糾纏結構：面積定律。很多人們關心的量子體系的兩部分之間的糾纏熵僅僅正比于其邊界的大小，這使得利用經典計算機高效而精確地研究這些量子多體問題成為可能。有意思的是，量子態所遵循的面積定律還和黑洞的熵有著深刻的聯系。從量子信息的視角審視引力、蟲洞以及量子混沌等現象，甚至有可能加深我們關于時空的本源的理解。國際上關于這方面的研究開展得如火如荼。美國的Simons 基金會支持了一項專注于此的合作研究項目。

量子糾纏的深遠影響并沒有就此止步，一些***的研究進展表明，它對機器學習(Machine Learning)中的一些問題也可能有啟發和指導意義。機器學習的研究目標是讓計算機獲得一定程度的智能，不需要過多的人為干預就可以高效地解決實際問題。通常，這種看似神奇的能力是從大量樣本的學習中獲得的。由于近年來算法和硬件的快速發展以及大量的數據積累，機器學習取得了一系列令人振奮的成果。特別是2016 年3 月Google DeepMind 所制造的AlphaGo 程序戰勝了世界圍棋冠軍李世乭，使得以深度學習(Deep Learning)為代表的新一代機器學習技術走進了大眾的視野。如今，機器學習在圖像和語音識別、機器翻譯、計算廣告、推薦系統等人類生活的方方面面都扮演著日趨重要的角色。而它的應用也在逐漸向天文、物理、化學、材料、生物、醫藥等眾多科學研究領域滲透。具體到本文作者所工作的領域：將機器學習方法應用于量子多體問題，可以從高維空間紛雜的微觀構型數據中提取出關鍵的物理信息。而將機器學習的思想與傳統計算途徑相結合，為解決凝聚態和統計物理中的疑難問題提供了新思路。最近的一些嘗試包括使用機器學習方法探測相變和分類物質相，探索使用人工神經網絡作為量子體系的試探波函數等等。這些嘗試讓物理學家們有機會仔細審視機器學習領域的核心思想和技術。本文介紹的就是這一方向上新涌現出的一個研究思路：從量子糾纏的視角審視深度學習，從而反饋機器學習的發展。

2. 深度學習和量子多體物理中的函數近似

深度學習究竟在做什么?用最簡短的話概括，就是函數近似(Function Approximation)。函數近似的目的是用高效經濟的方式盡可能精確地描述復雜的函數映射。實際問題中的目標函數可能是圖像識別應用中從微觀像素到圖片類別的映射，可能是AlphaGo 中圍棋的局面到最終勝率的估計，也可能是Atari 視頻游戲中的畫面到***控制策略的映射等等。讀者也許已經看出來了，以上這幾個函數恐怕都很難用一個簡潔的方式表達。即使考慮一個極端簡化的情形：怎樣描述有N 個二進制自變量的多元函數?原則上，我們當然可以存儲一個2N 行的表格來精確表達這樣一個函數。這個表格的每一行對應了一種可能的輸入和輸出，函數的計算也就等價于查表。可是只要N ≳ 70 ，即使用上全世界所有的存儲介質，我們也沒有能力存下這張表格，更不要說對它進行高效的查找了。

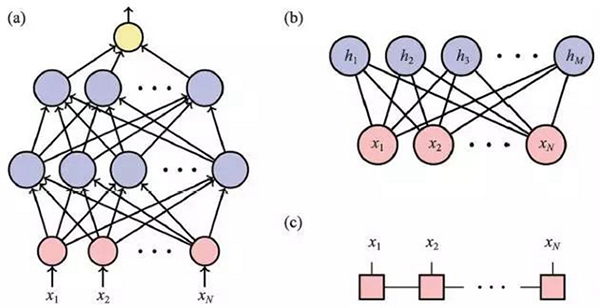
機器學習中的連接主義學派(Connectionism)提倡使用人工神經網絡(Artifical Neural Network)來解決這類函數近似問題。連接主義強調復雜的現象(比如智能)不來自于相對簡單的組成單元，而來自于這些單元之間的連接。圖1(a)，(b)展示了兩種常見的人工神經網絡結構。圖1(a)是前饋神經網絡(Feedforward Neural Network)。圖中的每一個藍色圓圈代表一個人工神經元，它接受上一層結果作為輸入，加權求和之后通過一個非線性的激活函數傳遞給下一層。可見，前饋神經網絡是通過多層非線性函數的嵌套來表達復雜的多元函數的。而圖1(b)顯示了另外一種函數參數化方式：限制玻爾茲曼機(Restricted Boltzmann Machine)。從名字就可以看出，玻爾茲曼機和統計物理有著十分密切的關聯。我們可以將它理解成一個統計力學系統，其中包含了兩組相互作用的隨機變量：顯變量(紅色)和隱變量(藍色)。“玻爾茲曼機”的名字來源于這些隨機變量的聯合概率分布遵循統計物理中的玻爾茲曼分布。而“限制”這個詞來源于圖1(b)中所示的特殊網絡結構：所有連接都僅在顯層和隱層之間。和全連接的玻爾茲曼機相比，這樣的結構可以極大地提高計算效率。而對于一個只關心顯變量的觀察者來說，即便顯層內部沒有直接的相互作用，隱層神經元所誘導的有效相互作用還是可以將它們關聯起來。

圖1 幾種參數化多元函數的方式(a)前饋神經網絡;(b)限制玻爾茲曼機;(c)矩陣乘積態

與使用一個2N 行的表格相比，圖1(a)，(b)中所示的兩類網絡結構都可以用少得多的參數近似表達復雜的多元函數。在實際應用中，我們可以通過調節前饋神經網絡中的權重參數，使得它學會從圖片像素信息中分辨其中物體的種類。或者，我們也可以調節限制玻爾茲曼機中隨機變量之間的相互作用強度，使得顯變量的概率分布盡可能重現目標數據集的分布。訓練好的玻爾茲曼機可以生成更多遵循目標概率分布的新樣本。以上兩類任務分別對應了判別型學習(Discriminative Learning) 和生成型學習(Generative Learning)。打個比方，判別型學習相當于學會認字，而生成型學習的目標是學會寫字。正如費曼在他的黑板上留下的那句名言“What I can not create,I do not understand”，學會寫可比學會讀困難得多，也要求更深層次的理解。判別型學習支撐著大量當下成功的商業應用，而探索生成型學習的模型和算法則代表了深度學習研究的前沿和未來。

在實際應用中，人們希望使用通用的人工神經網絡結構表達盡可能復雜多變的函數形式。這自然引出一個問題：圖1(a)，(b)所示的網絡都能夠表達什么樣的函數形式?為此，人們證明了所謂的“普適表示定理”：隨著網絡中隱層神經元個數的增加，圖1(a)中所示的前饋神經網絡結構(即使只有單個隱層)可以任意逼近任何的連續函數。類似地，通過增加圖1(b)中限制玻爾茲曼機的隱層神經元數目，它也可以表達關于顯變量任意復雜的概率分布函數。然而遺憾的是，針對一個具體的函數近似問題，以上這些普適表示定理沒辦法告訴我們至少需要多少隱層神經元，也沒辦法告訴我們究竟如何確定這些神經元之間的連接權重。而現實中我們關心的首要問題就是：給定有限的計算時間和存儲資源，應該如何***地分配它們呢?

經過多年的摸索實踐，人們有一個關鍵的發現：在參數個數一樣的情況下，深層的神經網絡比淺層的網絡具有更強的表達能力。訓練越來越深的神經網絡來近似表達復雜的函數形式，是深度學習這個名詞中“深度”的來源。當然，神經網絡的表達能力也并不是越強越好。過于復雜的網絡結構不僅增加了計算量，還可能造成神經網絡過擬合(Over-fitting)，這就是典型的“過猶不及”。神經網絡的表達能力***是與需要描述的函數的復雜程度相匹配。為此，人們設計出了種類繁多的神經網絡結構。很多這些結構設計主要由工程實踐經驗驅動，這使得深度學習得到了“經驗主義”的名聲。利用人工神經網絡作函數近似的初衷是利用它們的通用性，不需要太多的人為介入就可以自動尋找到數據中的關鍵特征(Feature)。可當神經網絡結構變得越來越多樣之后，面臨網絡的人為選擇問題，我們又回到了起點。

因此，人們迫切需要一些更具指導意義的判別標準，來幫助我們定量化地界定神經網絡的表達能力和數據集的復雜程度，以便在不同結構的神經網絡之間作出比較和取舍。為此我們需要對于神經網絡所表達的對象——現實世界中的多元函數——有更深刻的理解。在我們前面的例子中，雖然所有可能的輸入原則上有2N 種，但典型的輸入其實通常遵循某一特定分布。關于目標數據分布和函數性質的先驗知識(Prior Knowledge)有助于指導我們設計合適的神經網絡結構。一個最明顯的先驗知識就是函數的對稱性。比如，在圖像識別的例子中，圖片的種類與其中物體的具體位置無關。類似地，對于圍棋局面的估值對盤面構型也應該具有反演和旋轉不變性。在圖1(a)的網絡中實現這些限制，我們就得到了卷積神經網絡(Convolutional Neural Network)。它使用局域感知區(Local Receptive Fields)掃描整張圖片尋找特征，通過不同感知區共享權重來保證函數的不變性。如何發掘和利用更多類似的“先驗知識”是深度學習成功的關鍵。

與上述例子類似，量子物理的研究中也常常使用到函數近似。比如，一個量子自旋體系的波函數無非是一個關于自旋構型的多元函數。和深度學習中的目標一樣，我們也希望使用盡量簡單的參數化方式和盡量少的參數描述盡可能復雜的波函數。總結一句話，那就是“天網恢恢，疏而不漏”。圖1(c)顯示量子多體物理研究中常用的一種參數化波函數的方法：矩陣乘積態(Matrix Product State)。它的基本組成單元是紅色方塊所示的三階張量。豎線代表物理指標，而方塊之間的橫線則稱為“虛擬鍵”(Vitual Bond)。橫線之間的連接代表對于虛擬鍵指標的求和。不難猜測，隨著虛擬鍵維數(Vitual Bond Dimension)的增大，矩陣乘積態可以表達關于物理指標愈加復雜的函數。除了增加虛擬鍵維數，另一種增加矩陣乘積態表達能力的方法是將圖1(c)中所示的方塊推廣成為更高階的張量，也就是增加虛擬鍵的個數。將所有虛擬鍵連接起來，求和完所有的內部張量指標，就得到了前文提到的張量網絡態。和深度學習中種類繁多的人工神經網絡結構一樣，物理學家也發明了很多不同結構的張量網絡態以及相對應的算法。然而，和深度學習不同的是，物理學家們對于張量網絡的表達能力有著更為定量化的理解：關鍵在于量子糾纏!切割一個張量網絡態所斷開的虛擬鍵的個數和維數與這個網絡能夠描述的糾纏熵直接相關。而另一方面，雖然量子多體問題的希爾伯特空間非常大，但幸運的是大多數人們感興趣的量子態只是其中的一個很小的子集。這些態的量子糾纏熵并不是任意的，而是遵循前文提到的面積定律。張量網絡態恰好抓住了物理問題的這個重要特性，因而獲得成功。在實際研究中，物理學家們通常針對具體物理問題的糾纏大小和模式來靈活選擇設計張量網絡態結構。在這個意義下，量子糾纏其實就是指引物理學家們應用張量網絡研究量子多體問題的“先驗知識”。

3. 深度學習助力量子物理

從函數近似的觀點看，深度學習和量子物理之間的聯系非常顯然。即便在上一次連結主義學派研究的低潮期，也曾有過一些使用人工神經網絡作為量子體系的變分波函數的嘗試。最近，Carleo 和Troyer嘗試使用限制玻爾茲曼機作為量子自旋體系的多體變分波函數，得到了非常精確的基態能量和非平衡動力學的結果。值得注意的是，傳統的限制玻爾茲曼機只能表達取值為正的概率分布函數，為了讓它們適合于描述帶有相位信息的波函數，Carleo 等將限制玻爾茲曼機的參數推廣到復數域。另外，實際計算中Carleo 等采用的函數形式其實是多個共享權重的限制玻爾茲曼機的乘積。這樣的結構等價于一個單隱層的卷積神經網絡，從而在結構上保證了物理體系的空間平移不變性。Carleo 和Troyer 的結果激起了人們極大的興趣，沿著這個思路往下：類似的人工神經網絡還能夠描述其他豐富多彩的物質態嗎?

對于這個問題， 鄧東靈、李曉鵬和Das Sarma給出了一個構造性的回答。他們舉例說明限制玻爾茲曼機的函數形式可以表達幾種受到普遍關注的拓撲態。而蔡子直接訓練圖1(a)所示的前饋神經網絡以測試它們能否學會表達一些典型的玻色子、費米子、阻挫磁性態的波函數。這些嘗試進一步展示了人工神經網絡作為量子多體波函數的潛力。可是，是否有更一般的理論定量地描述這類人工神經網絡變分波函數的優勢和局限性呢?為了回答這些問題，鄧東靈等人 研究了限制玻爾茲曼機的糾纏表達能力。他們發現稠密連接的限制玻爾茲曼機原則上能夠承載超越面積定律的量子糾纏。本文作者與謝海東、向濤利用等價變換的思路，在玻爾茲曼機和張量網絡態之間建立起了一座橋梁。這樣就可以通過分析對應的張量網絡態來回答前面關于玻爾茲曼機的種種問題。我們發現恢復平移不變的波函數構造是Carleo 等計算成功的一個關鍵點，這樣的構造在不增加變分參數的情況下巧妙地增加了變分波函數表達能力的上限。郜勛和段路明則從計算復雜性理論的角度分析論證了限制玻爾茲曼機的局限性，并指出深層的玻爾茲曼機可以高效地描述幾乎所有已知的量子態。他們的工作表明糾纏熵并非刻畫表達能力的唯一標準。還需要注意的是，更強的表達能力并不意味著在實際計算中能夠找得到更好的函數近似。另外，黃溢辰和Moore也研究了玻爾茲曼機在量子多體問題中的表達能力。以上這些理論發現，為設計更經濟高效的量子多體試探波函數提供了方向性指引。深度學習的領軍人物Yann LeCun也注意到了這一系列來自物理學領域的工作。他在Facebook 上分享了自己對于量子糾纏、黑洞熵以及張量網絡態的理解，并在***總結道：“迷人的聯系”。

4. 量子糾纏指引深度學習

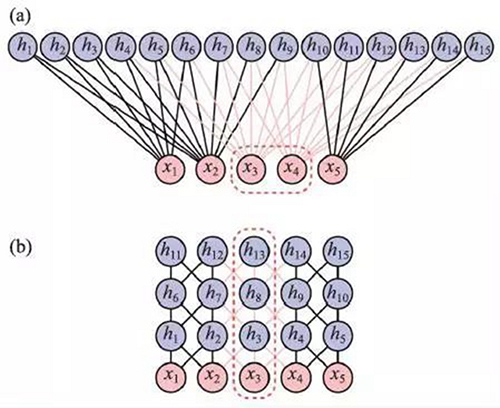
上述這些工作的研究思路是使用神經網絡近似量子多體波函數。有趣的是，使用逆向思維，量子多體物理也能夠幫助回答一些關于深度學習的問題。比如，我們可以從量子糾纏的視角來說明深度學習中的深度為什么重要。考慮圖2 中所示的兩個玻爾茲曼機，它們的隱層神經元個數和權重參數個數都完全相等。不同之處在于圖2(a)的隱層神經元呈淺層扁平化排列，而在圖2(b)中隱層神經元沿縱深方向排列成了層級結構。

圖2

圖2兩個不同架構，但參數個數相等的玻爾茲曼機(a)限制玻爾茲曼機;(b)深層玻爾茲曼機。紅色虛線框中的神經元承載了網絡左右部分的糾纏。一旦去除它們，網絡就分成了獨立的兩部分

為了分析比較圖2 中兩種網絡表達能力的優劣，我們按照文獻的思路將它們分別轉化成矩陣乘積態。由于是等價轉換，相應的矩陣乘積態的虛擬鍵維數限定了原來的玻爾茲曼機承載糾纏能力的上限。而根據文獻，要估計對應的虛擬鍵維數，只需要檢查在玻爾茲曼機中去除多少個神經元就可以將網絡從兩側斷開。如圖2 中虛線方框所示，深層玻爾茲曼機所對應的虛擬鍵維數更大，從而能夠比淺層的玻爾茲曼機負載更大的糾纏。以上的分析僅依賴于玻爾茲曼機的結構而不涉及到任何權重的數值信息。通過這樣的分析，我們從量子糾纏的角度說明了深層結構的重要性：深層玻爾茲曼機在擁有同樣參數個數的情況下具有相對更強的表達能力上限。這里，張量網絡態不僅僅是一個分析手段。作為一個副產品，我們也理解了它與玻爾茲曼機在函數近似上的各自優缺點。比如，為了表達同樣的量子態，玻爾茲曼機所用的參數個數可以比張量網絡態少得多。然而，對于某些特定狀態使用限制玻爾茲曼機表達卻不如張量網絡態方便。

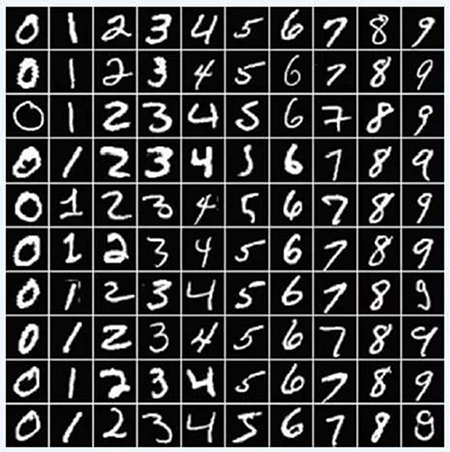
除了幫助分析神經網絡的表達能力，量子糾纏也可以作為深度學習應用的“先驗知識”：它定量地描述數據集的復雜度，并相應地指導設計人工神經網絡的結構。作為一個例子，讓我們考慮機器學習里的一個典型數據集：MNIST。如圖3 所示，MNIST中包含六萬張形態各異的手寫數字圖片。每一張都是28 × 28 的黑白圖像，其像素灰度取值0~255 。所有可能圖像的數目是一個天文數字： 25628×28 。然而，可以想象，真正有意義的手寫數字圖片只占據著這個巨大無比的“像素空間”中的一個小角落。聯想到前文所述，大多數物理上有興趣的量子態同樣僅僅占據希爾伯特空間的一個小角落。我們可以將MNIST中的圖片看作是對于某一量子波函數測量所得的構型快照。類比于對量子體系的分析，我們可以將每張圖片切成兩半，然后研究兩部分之間的量子糾纏。注意，如此定義的糾纏熵是對于整個數據集的分布而言的，并非對于單張圖片。數據集的糾纏特征指導我們在學習的過程中合理地分配資源。比如，注意到MNIST 數據集中每一張圖片的邊緣都是黑色的。這意味著圖片邊緣像素的取值不依賴于任何其他像素，從而不與它們形成糾纏。假如使用玻爾茲曼機來學習這樣的概率分布，就完全不需要使用隱變量來傳導它們之間的關聯。而另一方面，遮住MNIST圖片的一半，還能夠猜測出另一半大致的模樣。這就意味著圖片的這兩部分之間存在糾纏。糾纏熵的具體數值定量地告訴我們至少需要多少隱層神經元，以及怎樣的連接結構才能描述好這樣的數據集。

圖3 MNIST數據集中的一些樣本

曾獲得英特爾國際科學與工程大獎的少年Henry W. Lin 和MIT 的宇宙學家Max Tegmark 等合作指出，深度學習成功的關鍵不僅僅依賴于數學，更依賴于物理學規律。任何我們關心的實際數據集——無論是自然圖像還是語音信號——都是現實世界的反映。這也意味著它們通常表現出局域關聯、存在對稱性、呈現層級結構等特征。在本文作者看來，量子糾纏正可以定量化地挖掘和利用這些來自于物理定律的先驗知識。雖然，自然數據集的糾纏熵未必遵循面積定律，但它們離***糾纏的飽和值還應該差得遠。這啟發我們借用處理量子多體問題的思路，針對數據集的特點相應地設計合適的函數近似手段。讀者也許會感到奇怪，絕大多數現實應用中遇到的數據不都是經典的嗎?為什么非要引入量子糾纏的概念呢?經典信息論難道不夠用嗎?這里我們援引美國計算機科學家和量子信息學家Scott Aaronson 的觀點：將量子力學看作是經典概率論的數學推廣，而量子糾纏就是一個描述多參數函數性質的實用數學工具。文獻就是采用類似的研究思路使用量子糾纏來分析刻畫現實世界中的復雜網絡的。

以上的討論都是針對生成型學習而言的，那么，量子糾纏對于理解判別型的學習是否也有類似的幫助呢?考慮到深層的前饋神經網絡在現實世界中的廣泛應用，這是目前深度學習研究的一個熱點問題。這方面一個很有啟發的工作來自計算物理學家Stoudenmire和生物物理學家Schwab，他們成功訓練了一個矩陣乘積態來識別MNIST 數據集中的數字。他們的成功說明，從MNIST的像素到數字標記的函數映射的糾纏熵看起來并不大，完全可以被矩陣乘積態有效描述。無獨有偶，耶路撒冷希伯來大學的計算機科學家Amnon Shashua 所領導的團隊一直致力于使用張量分析的手段研究人工神經網絡。經過一系列前期工作的鋪墊，他們的注意力最近也被吸引到量子糾纏這個概念上。2017 年4 月初，Shashua 等人在arXiv 上貼出一篇題為“Deep Learning and Quantum Entanglement: Fundamental Connections with Implications to Network Design”的長文。這篇論文的***作者Yoav Levine 碩士期間在以色列的魏茨曼科學院(Weizmann Institute of Science)學習理論凝聚態物理，現在則是Shashua的博士生。在這篇文章中，Levine 等人采用與文獻類似的策略，將一類特殊的卷積神經網絡轉化為張量網絡態。這樣就可以通過對于張量網絡的最小切割(Min-Cut)分析來確定原來的人工神經網絡的糾纏表達能力了。作為一個具體的例子，他們考慮了“上寬下窄”和“上窄下寬”兩種結構的卷積神經網絡，并從理論上證明其性能的優劣取決于目標數據集的糾纏特性。他們在MNIST數據集上設計數值實驗，也的確驗證了這些理論預言。

可見，在深度學習與量子多體物理的交界處正在形成一個新興研究方向，量子糾纏正是連接它們的橋梁。一些嗅覺敏銳的研究者已經意識到了對方的思想、方法和技術對于本領域的幫助，正在積極地相互學習。預計隨著更多思維活躍的研究者的加入，深度學習和量子多體物理的研究會碰撞出更加燦爛的火花。

5. 結語

量子多體物理和深度學習的相遇也許本不應使人驚訝，畢竟，這兩個領域都關心大量微觀自由度組成的復雜體系中涌現出來的宏觀現象。人們為了認識自然界豐富多彩的量子物態所形成的工具，也許可以幫助我們設計出更智能的人工神經網絡和學習算法。“量子機器學習”(Quantum Machine Learning)是一個正在蓬勃發展的領域，本文僅介紹了其中的冰山一角。感興趣的讀者可參閱《物理》雜志上的介紹文章和最近的綜述。

愛因斯坦有一句名言：“自然是微妙的，可她沒有惡意”。隱藏在這個紛繁復雜的世界背后的結構算得上是微妙吧。可一旦抓住訣竅，居然可以用幾行簡潔美妙的公式理解。深度學習是不是能幫我們捕捉自然的善意呢?我們把這個問題放在這里，期待量子物理和機器學習的邂逅可以幫助我們發現更多自然的微妙!