今天很多現(xiàn)有的深度學習系統(tǒng)都是基于張量代數(shù)(tensor algebra)而設計的，但是張量代數(shù)不僅僅只能用于深度學習。本文對張量進行了詳細的解讀，能幫你在對張量的理解上更進一步。

近段時間以來，張量與新的機器學習工具(如 TensorFlow)是非常熱門的話題，在那些尋求應用和學習機器學習的人看來更是如此。但是，當你回溯歷史，你會發(fā)現(xiàn)一些基礎但強大的、有用且可行的方法，它們也利用了張量的能力，而且不是在深度學習的場景中。下面會給出具體解釋。

如果說計算是有傳統(tǒng)的，那么使用線性代數(shù)的數(shù)值計算就是其中最重要的一支。像 LINPACK 和 LAPACK 這樣的包已經(jīng)是非常老的了，但是在今天它們?nèi)稳环浅姶蟆Ｆ浜诵模€性代數(shù)由非常簡單且常規(guī)的運算構(gòu)成，它們涉及到在一維或二維數(shù)組(這里我們稱其為向量或矩陣)上進行重復的乘法和加法運算。同時線性代數(shù)適用范圍異常廣泛，從計算機游戲中的圖像渲染到核武器設計等許多不同的問題都可以被它解決或近似計算，

關鍵的線性代數(shù)運算：在計算機上使用的最基礎的線性代數(shù)運算是兩個向量的點積(dot product)。這種點積僅僅是兩個向量中相關元素的乘積和。一個矩陣和一個向量的積可以被視為該矩陣和向量行(row)的點積，兩個矩陣的乘積可以被視為一個矩陣和另一個矩陣的每一列(column)進行的矩陣-向量乘積的和。此外，再配上用一個值對所有元素進行逐一的加法和乘法，我們可以構(gòu)造出所需要的線性代數(shù)運算機器。

計算機之所以可憑極快速度求出用線性代數(shù)編寫的程序值，部分原因是線性代數(shù)具有規(guī)律性。此外，另一個原因是它們可以大量地被并行處理。完全就潛在性能而言，從早期的 Cray-1(譯者注：Cary-1 是世界上最早的一臺超級計算機，于 1975 年建造，運算速度每秒 1 億次)到今天的 GPU 計算機，我們可以發(fā)現(xiàn)性能增長了超過 30000 倍。此外，當你要考慮用大量 GPU 處理集群數(shù)據(jù)時，其潛在的性能，在極小成本下，比曾經(jīng)世上最快速的計算機大約高出一百萬倍。

然而，歷史的模式總是一致的，即要想充分利用新的處理器，我們就要讓運算越來越抽象。Cray-1 和它向量化的后繼者們需要其運行程序能夠使用向量運算(如點積)才能發(fā)揮出硬件的全部性能。后來的機器要求要就矩陣-向量運算或矩陣-矩陣運算來將算法形式化，從而方可盡可能地發(fā)揮硬件的價值。

我們現(xiàn)在正站在這樣一個結(jié)點上。不同的是我們沒有任何超越矩陣-矩陣運算的辦法，即：我們對線性代數(shù)的使用已達極限。

但是，我們沒有必要把自己限制在線性代數(shù)上。事實證明，我們可以沿著數(shù)學這棵大樹的枝葉往上再爬一段。長期以來，人們都知道在數(shù)學抽象的海洋中存在著比矩陣還要大的魚，這其中一個候選就是張量(tensor)。張量是廣義相對論重要的數(shù)學基礎，此外它對于物理學的其它分支來說也具有基礎性的地位。那么如同數(shù)學的矩陣和向量概念可被簡化成我們在計算機中使用的數(shù)組一樣，我們是否可以將張量也簡化和表征成多維數(shù)組和一些相關的運算呢?很不幸，事情沒有那么簡單，這其中的主要原因是不存在一個顯而易見且簡單的(如在矩陣和向量上類似的)可在張量上進行的一系列運算。

然而，也有好消息。雖然我們不能對張量使用僅幾個運算。但是我們可以在張量上寫下一套運算的模式(pattern)。不過，這還不不夠，因為根據(jù)這些模式編寫的程序不能像它們寫的那樣被充分高效地執(zhí)行。但我們還有另外的好消息：那些效率低下但是編寫簡單的程序可以被(基本上)自動轉(zhuǎn)換成可非常高效執(zhí)行的程序。

更贊的是，這種轉(zhuǎn)換可以無需構(gòu)建一門新編程語言就能實現(xiàn)。只需要一個簡單的技巧就可以了，當我們在 TensorFlow 中寫下如下代碼時：

v1 = tf.constant(3.0) 
v2 = tf.constant(4.0) 
v3 = tf.add(node1, node2) 

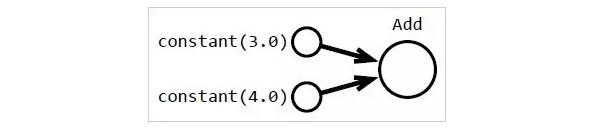
實際情況是，系統(tǒng)將建立一個像圖 1 中顯示的數(shù)據(jù)結(jié)構(gòu)：

圖 1

圖 1：上方的代碼被轉(zhuǎn)譯成一個可被重建的數(shù)據(jù)結(jié)構(gòu)，而且它會被轉(zhuǎn)成機器可執(zhí)行的形式。將代碼轉(zhuǎn)譯成用戶可見的數(shù)據(jù)結(jié)構(gòu)可讓我們所編寫的程序能被重寫從而更高效地執(zhí)行，或者它也可以計算出一個導數(shù)，從而使高級優(yōu)化器可被使用。

該數(shù)據(jù)結(jié)構(gòu)不會在上面我們展示的程序中實際執(zhí)行。因此，TensorFlow 才有機會在我們實際運行它之前，將數(shù)據(jù)結(jié)構(gòu)重寫成更有效的代碼。這也許會牽涉到我們想讓計算機處理的小型或大型結(jié)構(gòu)。它也可生成對我們使用的計算機 CPU、使用的集群、或任何手邊可用的 GPU 設備實際可執(zhí)行的代碼。對它來說很贊的一點是，我們可以編寫非常簡單但可實現(xiàn)令人意想不到結(jié)果的程序。

然而，這只是開始。

做一些有用但不一樣的事

TensorFlow 和像它一樣的系統(tǒng)采用的完全是描述機器學習架構(gòu)(如深度神經(jīng)網(wǎng)絡)的程序，然后調(diào)整那個架構(gòu)的參數(shù)以最小化一些誤差值。它們通過創(chuàng)建一個表征我們程序的數(shù)據(jù)結(jié)構(gòu)，和一個表征相對于我們模型所有參數(shù)誤差值梯度的數(shù)據(jù)結(jié)構(gòu)來實現(xiàn)這一點。這個梯度函數(shù)的存在使得優(yōu)化變得更加容易。

但是，雖然你可以使用 TensorFlow 或 Caffe 或任何其它基本上同樣工作模式的架構(gòu)來寫程序，不過你寫的程序不一定要去優(yōu)化機器學習函數(shù)。如果你寫的程序使用了由你選擇的包(package)提供的張量標注，那它就可以優(yōu)化所有類型的程序。自動微分和***進的優(yōu)化器以及對高效 GPU 代碼的編譯對你仍然有利。

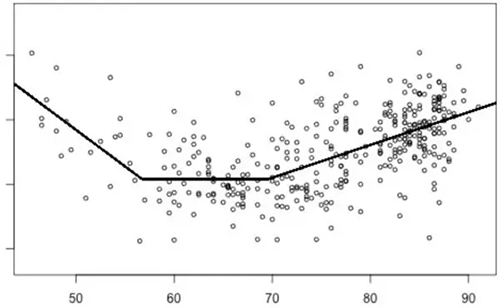
舉個簡例，圖二給出了一個家庭能耗的簡單模型。

圖 2

圖 2：該圖顯示了一間房子的日常能耗情況(圓圈)，橫軸代表了溫度(華氏度)。能耗的一個分段線性模型疊加在了能耗具體數(shù)據(jù)上。模型的參數(shù)按理來說會形成一個矩陣，但是當我們要處理上百萬個模型時，我們便可以用到張量。

該圖顯示了一間房子的能耗使用情況，并對此進行了建模。得到一個模型不是什么難事，但是為了找出這個模型，筆者需要自己寫代碼來分別對數(shù)百萬間房子的能耗情況進行建模才行。如果使用 TensorFlow，我們可以立即為所有這些房子建立模型，并且我們可以使用比之前得到這個模型更有效的優(yōu)化器。于是，筆者就可以立即對數(shù)百萬個房間的模型進行優(yōu)化，而且其效率比之前我們原始的程序要高得多。理論上我們可以手動優(yōu)化代碼，并且可以有人工推導的導數(shù)函數(shù)。不過完成這項工作所需要的時間，以及更重要的，調(diào)試花費的時間會讓筆者無法在有限時間里建立這個模型。

這個例子為我們展示了一個基于張量的計算系統(tǒng)如 TensorFlow(或 Caffe 或 Theano 或 MXNet 等等)是可以被用于和深度學習非常不同的優(yōu)化問題的。

所以，情況可能是這樣的，對你而言***用的機器學習軟件除了完成機器學習功能以外還可以做很多其它事情。

本文作者為 MapR Technologies 的***應用架構(gòu)師 Ted Dunning。

原文：http://www.kdnuggets.com/2017/06/deep-learning-demystifying-tensors.html

【本文是51CTO專欄機構(gòu)“機器之心”的原創(chuàng)譯文，微信公眾號“機器之心( id: almosthuman2014)”】

戳這里，看該作者更多好文