教你從頭到尾徹底理解KMP算法
本文參考:數據結構(c語言版) 李云清等編著、算法導論
引言:
在文本編輯中,我們經常要在一段文本中某個特定的位置找出 某個特定的字符或模式。
由此,便產生了字符串的匹配問題。
本文由簡單的字符串匹配算法開始,經Rabin-Karp算法,***到KMP算法,教你從頭到尾徹底理解KMP算法。
來看算法導論一書上關于此字符串問題的定義:
假設文本是一個長度為n的數組T[1...n],模式是一個長度為m<=n的數組P[1....m]。
進一步假設P和T的元素都是屬于有限字母表Σ.中的字符。
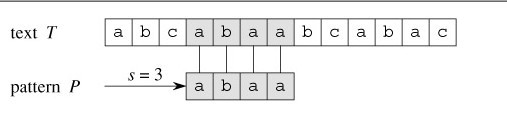
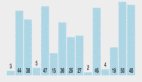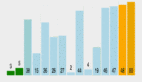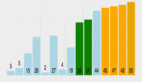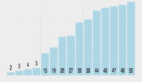
依據上圖,再來解釋下字符串匹配問題。目標是找出所有在文本T=abcabaabcaabac中的模式P=abaa所有出現。
該模式僅在文本中出現了一次,在位移s=3處。位移s=3是有效位移。
一、簡單的字符串匹配算法
簡單的字符串匹配算法用一個循環來找出所有有效位移,
該循環對n-m+1個可能的每一個s值檢查條件P[1....m]=T[s+1....s+m]。
NAIVE-STRING-MATCHER(T, P)
1 n ← length[T]
2 m ← length[P]
3 for s ← 0 to n - m
4 do if P[1 ‥ m] = T[s + 1 ‥ s + m]
//對n-m+1個可能的位移s中的每一個值,比較相應的字符的循環必須執行m次。
5 then print "Pattern occurs with shift" s
簡單字符串匹配算法,上圖針對文本T=acaabc 和模式P=aab。
上述第4行代碼,n-m+1個可能的位移s中的每一個值,比較相應的字符的循環必須執行m次。
所以,在最壞情況下,此簡單模式匹配算法的運行時間為O((n-m+1)m)。
--------------------------------
下面我再來舉個具體例子,并給出一具體運行程序:
對于目的字串target是banananobano,要匹配的字串pattern是nano,的情況,
下面是匹配過程,原理很簡單,只要先和target字串的***個字符比較,
如果相同就比較下一個,如果不同就把pattern右移一下,
之后再從pattern的每一個字符比較,這個算法的運行過程如下圖。
//index表示的每n次匹配的情形。
- #include<iostream>
- #include<string>
- using namespace std;
- int match(const string& target,const string& pattern)
- {
- int target_length = target.size();
- int pattern_length = pattern.size();
- int target_index = 0;
- int pattern_index = 0;
- while(target_index < target_length && pattern_index < pattern_length)
- (
- if(target[target_index]==pattern[pattern_index])
- {
- ++target_index;
- ++pattern_index;
- }
- else
- {
- target_index -= (pattern_index-1);
- pattern_index = 0;
- }
- }
- if(pattern_index == pattern_length)
- {
- return target_index - pattern_length;
- }
- else
- {
- return -1;
- }
- }
- int main()
- {
- cout<<match("banananobano","nano")<<endl;
- return 0;
- }
- //運行結果為4。
上面的算法進間復雜度是O(pattern_length*target_length),
我們主要把時間浪費在什么地方呢,
觀查index =2那一步,我們已經匹配了3個字符,而第4個字符是不匹配的,這時我們已經匹配的字符序列是nan,
此時如果向右移動一位,那么nan***匹配的字符序列將是an,這肯定是不能匹配的,
之后再右移一位,匹配的是nan***匹配的序列是n,這是可以匹配的。
如果我們事先知道pattern本身的這些信息就不用每次匹配失敗后都把target_index回退回去,
這種回退就浪費了很多不必要的時間,如果能事先計算出pattern本身的這些性質,
那么就可以在失配時直接把pattern移動到下一個可能的位置,
把其中根本不可能匹配的過程省略掉,
如上表所示我們在index=2時失配,此時就可以直接把pattern移動到index=4的狀態,
kmp算法就是從此出發。
二、KMP算法
1、 覆蓋函數(overlay_function)
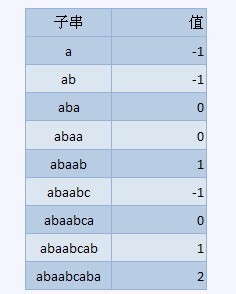
覆蓋函數所表征的是pattern本身的性質,可以讓為其表征的是pattern從左開始的所有連續子串的自我覆蓋程度。
比如如下的字串,abaabcaba
由于計數是從0始的,因此覆蓋函數的值為0說明有1個匹配,對于從0還是從來開始計數是偏好問題,
具體請自行調整,其中-1表示沒有覆蓋,那么何為覆蓋呢,下面比較數學的來看一下定義,比如對于序列
a0a1...aj-1 aj
要找到一個k,使它滿足
a0a1...ak-1ak=aj-kaj-k+1...aj-1aj
而沒有更大的k滿足這個條件,就是說要找到盡可能大k,使pattern前k字符與后k字符相匹配,k要盡可能的大,
原因是如果有比較大的k存在,而我們選擇較小的滿足條件的k,
那么當失配時,我們就會使pattern向右移動的位置變大,而較少的移動位置是存在匹配的,這樣我們就會把可能匹配的結果丟失。
比如下面的序列,
在紅色部分失配,正確的結果是k=1的情況,把pattern右移4位,如果選擇k=0,右移5位則會產生錯誤。
計算這個overlay函數的方法可以采用遞推,可以想象如果對于pattern的前j個字符,如果覆蓋函數值為k
a0a1...ak-1ak=aj-kaj-k+1...aj-1aj
則對于pattern的前j+1序列字符,則有如下可能
⑴ pattern[k+1]==pattern[j+1] 此時overlay(j+1)=k+1=overlay(j)+1
⑵ pattern[k+1]≠pattern[j+1] 此時只能在pattern前k+1個子符組所的子串中找到相應的overlay函數,h=overlay(k),如果此時pattern[h+1]==pattern[j+1],則overlay(j+1)=h+1否則重復(2)過程.
下面給出一段計算覆蓋函數的代碼:
- #include<iostream>
- #include<string>
- using namespace std;
- void compute_overlay(const string& pattern)
- {
- const int pattern_length = pattern.size();
- int *overlay_function = new int[pattern_length];
- int index;
- overlay_function[0] = -1;
- for(int i=1;i<pattern_length;++i)
- {
- index = overlay_function[i-1];
- //store previous fail position k to index;
- while(index>=0 && pattern[i]!=pattern[index+1])
- {
- index = overlay_function[index];
- }
- if(pattern[i]==pattern[index+1])
- {
- overlay_function[i] = index + 1;
- }
- else
- {
- overlay_function[i] = -1;
- }
- }
- for(i=0;i<pattern_length;++i)
- {
- cout<<overlay_function[i]<<endl;
- }
- delete[] overlay_function;
- }
- int main()
- {
- string pattern = "abaabcaba";
- compute_overlay(pattern);
- return 0;
- }
運行結果為:
-1
-1
0
0
1
-1
0
1
2
Press any key to continue
-------------------------------------
2、kmp算法
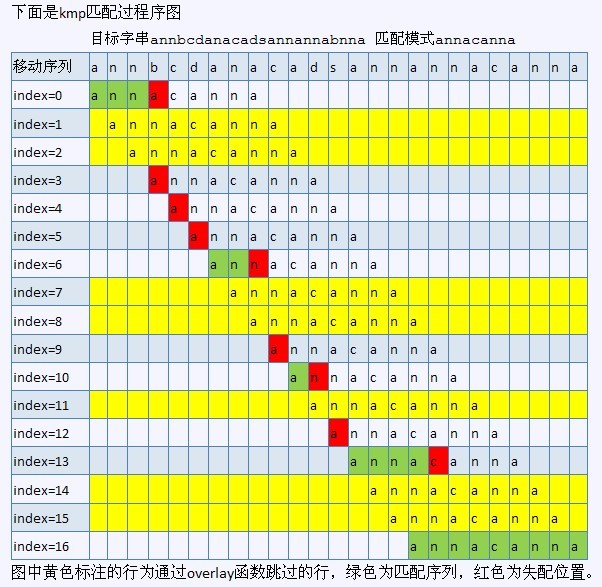
有了覆蓋函數,那么實現kmp算法就是很簡單的了,我們的原則還是從左向右匹配,但是當失配發生時,我們不用把target_index向回移 動,target_index前面已經匹配過的部分在pattern自身就能體現出來,只要動pattern_index就可以了。
當發生在j長度失配時,只要把pattern向右移動j-overlay(j)長度就可以了。
如果失配時pattern_index==0,相當于pattern***個字符就不匹配,
這時就應該把target_index加1,向右移動1位就可以了。
ok,下圖就是KMP算法的過程(紅色即是采用KMP算法的執行過程):
ok,***給出KMP算法實現的c++代碼:
- #include<iostream>
- #include<string>
- #include<vector>
- using namespace std;
- int kmp_find(const string& target,const string& pattern)
- {
- const int target_length = target.size();
- const int pattern_length = pattern.size();
- int * overlay_value = new int[pattern_length];
- overlay_value[0] = -1;
- int index = 0;
- for(int i=1;i<pattern_length;++i)
- {
- index = overlay_value[i-1];
- while(index>=0 && pattern[index+1]!=pattern[i])
- {
- index = overlay_value[index];
- }
- if(pattern[index+1]==pattern[i])
- {
- overlay_value[i] = index +1;
- }
- else
- {
- overlay_value[i] = -1;
- }
- }
- //match algorithm start
- int pattern_index = 0;
- int target_index = 0;
- while(pattern_index<pattern_length&&target_index<target_length)
- {
- if(target[target_index]==pattern[pattern_index])
- {
- ++target_index;
- ++pattern_index;
- }
- else if(pattern_index==0)
- {
- ++target_index;
- }
- else
- {
- pattern_index = overlay_value[pattern_index-1]+1;
- }
- }
- if(pattern_index==pattern_length)
- {
- return target_index-pattern_index;
- }
- else
- {
- return -1;
- }
- delete [] overlay_value;
- }
- int main()
- {
- string source = " annbcdanacadsannannabnna";
- string pattern = " annacanna";
- cout<<kmp_find(source,pattern)<<endl;
- return 0;
- }
- //運行結果為 -1.
三、kmp算法的來源
kmp如此精巧,那么它是怎么來的呢,為什么要三個人合力才能想出來。其實就算沒有kmp算法,人們在字符匹配中也能找到相同高效的算法。這種算法,最終 相當于kmp算法,只是這種算法的出發點不是覆蓋函數,不是直接從匹配的內在原理出發,而使用此方法的計算的覆蓋函數過程序復雜且不易被理解,但是一但找 到這個覆蓋函數,那以后使用同一pattern匹配時的效率就和kmp一樣了,其實這種算法找到的函數不應叫做覆蓋函數,因為在尋找過程中根本沒有考慮是 否覆蓋的問題。
說了這么半天那么這種方法是什么呢,這種方法是就大名鼎鼎的確定的有限自動機(Deterministic finite state automaton DFA),DFA可識別的文法是3型文法,又叫正規文法或是正則文法,既然可以識別正則文法,那么識別確定的字串肯定不是問題(確定字串是正則式的一個子 集)。對于如何構造DFA,是有一個完整的算法,這里不做介紹了。在識別確定的字串時使用DFA實在是大材小用,DFA可以識別更加通用的正則表達式,而 用通用的構建DFA的方法來識別確定的字串,那這個overhead就顯得太大了。
kmp算法的可貴之處是從字符匹配的問題本身特點出發,巧妙使用覆蓋函數這一表征pattern自身特點的這一概念來快速直接生成識別字串的DFA,因此對于kmp這種算法,理解這種算法高中數學就可以了,但是如果想從無到有設計出這種算法是要求有比較深的數學功底的。
原文:http://www.2cto.com/kf/201104/87381.html
作者聲明:個人July 對此24個經典算法系列,享有版權,轉載請注明出處。