五、如何遞，怎樣歸？

     很多人看完遞歸的原理之后會有這種感覺，喔，這個原理我懂了，然后再找一道其余的題目看一看能不能寫的出來，突然發現，我勒個去，還是不會。其實這種現象很普遍，所以如果你是這種的，也沒有什么好沮喪的，我敢保證你能看的懂遞歸的執行過程，基本上已經比30%的人要強了。所以我覺得，我寫一寫我對遞歸思維的理解好了。遞歸這個詞我的理解應該是傳遞和回歸，如何把自身的狀態傳遞下去和如何回歸到一個結果上是遞歸問題的基本思維方式。

      所謂如何傳遞，我覺得思維的難點是如何抽象出數學模型，如果是斐波那契數列那種有明確公式的話，很簡單，直接按照公式該怎么操作怎么操作，難得是只有敘述性語言的，比如這種題目：有一段樓梯n個階梯，你可以選擇一次上一個階梯，也可以選擇一次上兩個階梯，請問走到頂部一共有多少種走法？看似很高深吧？其實這就是斐波那契數列的一個變體而已。這種描述性的題目如果要抽象出數學模型，我覺得***的辦法就先列舉幾個試試，先看看有什么規律沒有，然后再猜想，再證明。你先看看你上2層樓梯有幾種方法，2層樓梯要么是1次性上去，要么分成兩步，一次性上一步，于是就是F（2）=2，如果只有一層和沒有呢，那明顯只有一種走法(一次上一層和不走），也就是F(0)=1,F(1)=1,下面，你要上第三層，你的辦法要么是從第二層上一層到第三層，要么是在***層上兩層到第三層，要么一層一層的走上去，這樣F(3)=3，看起來還是沒有什么規律，接著往下來，現在要上第四層了，那么讓我們換一種思維方式，怎樣到第四層呢？要么你在第三層到第四層，要么從第二層到第四層，為什么不說從***層到第四層呢？因為如果你把這個當作一種情況的話，你會發現在***層的時候，無論下一步你怎樣做都會回到上面兩種情況之中。所以到第四層的作法就是F(3)+F(2),因為你到了第三層或者到了第二層（如果你在第二層選擇上一層那么就會和在第三層的走法重合），后面的走法就確定了，不同的是前面的走法，也就是F(4)=5，現在讓我們增加點難度，如果你要到第n層，那么應該說***一步你有可能是從第n-1層走兩層上來的，也有可能是從第n層走兩層上來的，也就是說到第n層的走法決定于你怎么走到第n-1層和第n層的，所以這個走法應該是F(n)=F(n-1)+F(n-2)。

      還有一種不知道如何傳遞是不知道怎樣將遞歸算法轉換成程序，你知道怎樣用語言描述出遞歸，但是就是不知道怎樣用程序描寫出來，所以***的方式是找一段遞歸的程序，然后看他每一次遞歸的輸出。

     關于如何歸，就是要找到遞歸中止的條件，比如斐波那契數列那個，n=0就是數列的中止條件，別小看這個中止條件，如果不能找出這個中止條件或者定義錯誤的話，后果就是無限的遞歸，導致程序堆棧的崩潰，最終整個程序就很快的崩潰掉了。

     我們從一個簡單的開始，使用遞歸算法求***公約數，利用輾轉相除法,簡單的說就是對于兩個數m和n，利用公式gcd（m,n)=gcd(n,m%n)=

gcd(m%n,m%n%n),直到后面的余數為0為止，這是個有數學公式的比較明顯的遞歸模式，所以按照這個數學公式的邏輯，這個遞歸算法的回歸的話n==0的時候，所以這個算法很容易寫出來。

     代碼相當的簡單，思路要很清晰。那么，再來看一個二分搜索的好了，二分搜索是在已經排序好的數列里面尋找目標數，比如{1,2,...,10},這種，如果是尋找2，那么先求出這一組數的中值5，2比5小，從而轉到0-5這個部分，其中值是2,然后就找到了。這種搜索的過程也是一種不斷傳遞的過程，將某個數列的中值和要查找的目標值比較，如果比它小，就在數列的后半部分做同樣的操作，如果比它大，就在前半部分做相同的操作。那么這個回歸的條件是什么呢？應該說有兩個，一個是找到了，也就是某一個中值等于目標值，一個是沒有找到，可以定義為找到了***個元素和***一個元素還是沒有找到，那么也結束遞歸，其代碼如下:

int BinarySearch(int a[],int n,int low,int high) 
 { 
     int mid=(low+high)/2; 
     if(n==a[mid]) 
         return mid; 
     if((mid==high||mid==low)&&n!=a[mid]) 
         return 0; 
  
     if(n>a[mid]) 
           BinarySearch(a,n,mid+1,high); 
     else  
           BinarySearch(a,n,low,mid); 
       
 } 

     通過代碼可以看到思路和我上面語言描述的基本是一致的，這就是遞歸的好處，可以使得代碼更加清晰。

六、“高帥富”的裝備

      如果你看過一些時間復雜度可以到O(NLOGN）的排序算法，可以看到它們不僅效率高，代碼也很簡潔，因為使用遞歸使得很多復雜的過程變得簡單，使得某個算法可以更容易的實現出來，我先要說的是歸并排序。

     歸并排序簡單的將就是將一個數列不斷的平均分為兩個小數列，然后每個小數列獨立排序之后再合并在一起排序，也就是用若干有序的子序列得到一個有序的數列，為了說明，還是用一個例子好了，就用百度的這個例子好了：

如　設有數列{6，202，100，301，38，8，1}

初始狀態： [6] [202] [100] [301] [38] [8] [1]

            　　i=1 [6 202 ] [ 100 301] [ 8 38] [ 1 ]　 　　

                  i=2 [ 6 100 202 301 ] [ 1 8 38 ]　

            　　i=3　[ 1 6 8 38 100 202 301 ]  　

       整個過程就是不斷的劃分為子序列，不斷的用子序列排序，這明顯是一個遞歸的過程，傳遞的過程是不斷傳遞子序列，那么回歸條件是什么呢？貌似這里不太能夠看出來，從上面的過程可以大概看出來如果當數列的個數只有1的話，那么就要開始回歸了，所以我們采用了一個方法，既然需要找中間的那個值，那么就要保存左邊的索引和右邊的索引，利用這兩個索引，可以確定出數組中有多少個值，那么先看一下代碼吧。

void MergeSort(int numbers[],int array_size) 
{ 
    int* tmpArray =new int[array_size-1]; 
    MergeSort(numbers,tmpArray,0,array_size-1); 
 
} 
 
void MergeSort(int numbers[],int tmpArray[],int left,int right) 
{ 
    if(left<right) 
    { 
        int center=(left+right)/2; 
        cout<<"0"<<endl; 
        MergeSort(numbers,tmpArray,left,center); 
        cout<<"1"<<endl; 
        MergeSort(numbers,tmpArray,center+1,right); 
        cout<<"2"<<endl; 
        Merge(numbers,tmpArray,left,center+1,right); 
        cout<<"3"<<endl; 
    } 
} 
 
void Merge(int numbers[],int tmpArray[],int leftPos,int rightPos,int rightEnd) 
{ 
    int leftEnd=rightPos-1; 
    int tmpPos=leftPos; 
    int numElements=rightEnd-leftPos+1; 
 
    while(leftPos<=leftEnd&&rightPos<=rightEnd) 
    { 
        if(numbers[leftPos]<=numbers[rightPos]) 
            tmpArray[tmpPos++]=numbers[leftPos++]; 
        else 
            tmpArray[tmpPos++]=numbers[rightPos++]; 
    } 
    while(leftPos<=leftEnd) 
         tmpArray[tmpPos++]=numbers[leftPos++]; 
    while(rightPos<=rightEnd) 
         tmpArray[tmpPos++]=numbers[rightPos++]; 
 
    for(int i=0;i<numElements;i++,rightEnd--) 
         numbers[rightEnd]=tmpArray[rightEnd]; 
         
    for (int i = 0; i < numElements; i++){ 
            cout<<numbers[i]<<" "; 
        } 
        cout<<endl; 
} 

      代碼開始有些復雜了，真正有點算法的感覺了，先看看三個函數，***個函數沒有什么特別的含義，只是屏蔽掉一些細節而已，從第二個MergeSort開始，可以看到就像我們描述的思路那樣，***個是比較是否數組里只有一個值，需要回歸啦，然后求出中值，左邊的排序成有序的子序列，然后排序右邊的，***將兩個子序列合并起來，是不是思路特別的清晰？那么接下來看看Merge函數，如果有兩個有序的子序列如何將他們合并成一個？因為這兩個子序列都是有序的，記為子序列A和子序列B，A[0]到A[size-1]是有序的，B[0]到B[size-1]也是有序的，那么對比的過程就簡單了，不斷的對比不斷的合并就可以了。

      對于函數執行的遞歸過程，肯定很多人還是一頭霧水，這很正常，畢竟沒有一個清晰的直觀的認識，那么讓我們看看遞歸的每一步都是怎么走的吧。

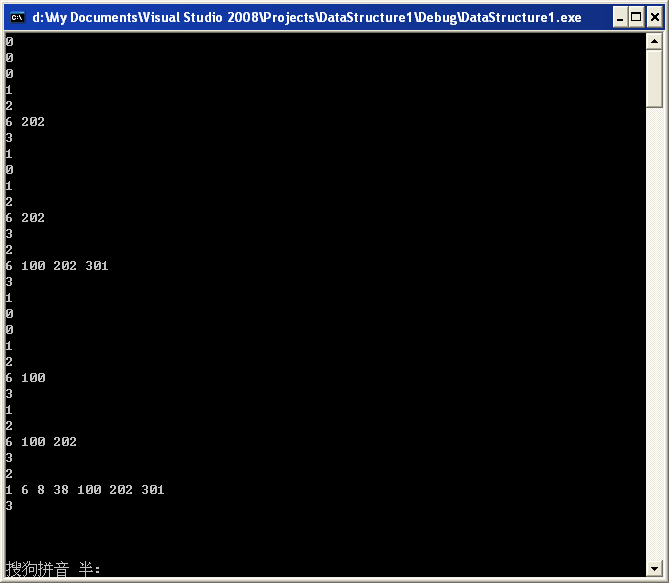
      對于百度給的那個例子，從頭看起，我們調用的代碼是 MergeSort(a,7); 所以，

1.   left最開始等于0，right等于6，進入MergeSort以后left<right，進入if，輸出0，center=3，調用   MergeSort(numbers,tmpArray,left,center);
1.1 left等于0，right等于center等于3，依然滿足left<right，進入if，輸出0，center=1，繼續調用   MergeSort(numbers,tmpArray,left,center);

1.2 left等于0，right等于center等于1，依然滿足left<right，進入if，輸出0，center=0，繼續調用   MergeSort(numbers,tmpArray,left,center);

1.3 left等于0，right等于center等于0，不滿足left<right，掉回1.2往下執行，到此步，輸出了三個0

1.2.1  left等于0，right等于center等于1，執行MergeSort(numbers,tmpArray,left,center);下一行語句，輸出1，執行       MergeSort(numbers,tmpArray,center+1,right);

1.2.2 left等于center+1等于1，right=1，不滿足left<right,回到1.2.1,執行MergeSort(numbers,tmpArray,center+1,right);下面的語句，輸出2，然后進入

 Merge(numbers,tmpArray,left,center+1,right);排序完成之后輸出3。

       以上是一次完整的遞歸過程，對著輸出可以看到這個過程的執行，作為理解遞歸的練習，完全可以對照著后面的輸出熟悉遞歸的過程，對于遞歸的執行，我覺得可以理解為執行到調用自己的函數的時候就不斷的困在自己的這個函數中，直到到達某一個條件時，被自己釋放，回到上一個過程才能進行，這個過程就像有的人失戀了，每天都和自己糾結，每天都在痛苦和不安中度過，這個過程中他是不能往下走的，一旦到某一個條件，比如時間慢慢的沖淡了感覺，他又可以繼續進行了。

原文鏈接：http://www.cnblogs.com/ZXYloveFR/archive/2012/09/26/2704241.html

【編輯推薦】