哪種語言將統(tǒng)治多核時代 再看函數(shù)式語言特性
譯文51CTO編輯推薦:Scala編程語言專題
【51CTO外電精選】最近這幾年,軟件開發(fā)語言可謂是層出不窮。在這些新的編程語言中,最多的就是函數(shù)式語言。本文將向你介紹函數(shù)式語言的概念、術(shù)語、方法以及幾種典型的函數(shù)式語言。本文面向的讀者是那些已經(jīng)懂得其它編程語言、但卻對函數(shù)式語言沒有了解的開發(fā)人員。
什么是函數(shù)式語言?
如果你已經(jīng)用面向?qū)ο蟮恼Z言(例如Java和C#)寫了很長時間的代碼,那么可能很難想象出另一種新的編程思維方式,而函數(shù)式語言恰恰做到了這一點。它的核心就是通過對算法進行功能分解,從而解決軟件問題。在函數(shù)式語言里,函數(shù)是首要的。如果你是Java陣營出身,那應該能理解到這之間的差異。在Java中,實現(xiàn)某種方法的唯一形式就是將其作為某個類的成員。
雖然最近風頭正勁的某些特殊語言引人注目,但是函數(shù)式語言其實也可以代表一門技術(shù),而不僅僅是一種語言。我們可以用函數(shù)式編程的方式,用面向?qū)ο蟮木幊陶Z言實現(xiàn)一般的功能(后面的章節(jié)里我們就會看到一個用函數(shù)式方法編寫的C#程序)。雖然這可以實現(xiàn),但是在稍大一點的程序中,我們很快就會感覺到缺乏表現(xiàn)力,反模式(anti-pattern)也隨之出現(xiàn)。試想一下,不用extend和implement關(guān)鍵字寫個上規(guī)模的Java程序有多痛苦。由于這些困難的存在,人們需要一種新的語言:一種函數(shù)式語言。
為何需要函數(shù)式語言?
很明顯,現(xiàn)代計算平臺上發(fā)生了一個重大變化,那就是多核技術(shù)的引入。除了上網(wǎng)本和PDA,我們甚至都找不出還采用單核處理器的臺式機和筆記本電腦了。我們正在向多核心,多處理器發(fā)展,并且所有跡象都表明這一趨勢將繼續(xù)下去。除了采用多核心之外,高運算量和高復雜度的算法應用都傾向于優(yōu)化使用圖形處理單元(GPU),從而提高并行性。歸納起來,從開發(fā)者的角度來說,這些都屬于并發(fā)問題的范疇。
我們大多數(shù)的編程語言都不容易實現(xiàn)并發(fā)。想想幾十年前,C語言程序里的錯誤處理直接就被代碼基底(code base)丟棄了。它與業(yè)務邏輯混在了一起。C函數(shù)成功后就將返回0 ,失敗則返回錯誤代碼。很明顯這不是很理想的辦法,但是C語言本身的表達能力限制了開發(fā)者們用其它方法來進行出錯處理。其他語言對此進行了改進,在C++或者Java中,出錯時會拋出異常,異常處理程序把出錯處理和正常事務處理分離開來。有些人可能會說這也算不上什么太好的辦法,但是這至少是個不小的進步了。在解決并發(fā)這個問題上,我們所掌握的技術(shù)的成熟度也和這差不多。如果想要在一個用面向?qū)ο笳Z言編程的程序里實現(xiàn)并行,那編寫起來真得費一番腦筋。像生成一個打印任務線程并不需要處理多少并發(fā)控制,但是往往它還會牽扯到進程間的狀態(tài)共享、顯示器的阻塞。隨著內(nèi)核數(shù)的增加,同時運行的線程數(shù)可能進一步增大,系統(tǒng)的效率也將隨之降低。這時,我們就需要一種新的語言,讓我們能從這些細節(jié)工作中抽身出來,以更好地利用并發(fā)。
函數(shù)式語言已經(jīng)在簡化并行開發(fā)中證明了它的作用, 這得益于它既不用共享內(nèi)存,也不會產(chǎn)生副作用(side effect)的函數(shù)。進一步深入函數(shù)式語言,你就會發(fā)現(xiàn)它讓開發(fā)者從并發(fā)這個概念中抽身出來了,讓開發(fā)者不用老是想著現(xiàn)在CPU是在并發(fā)作業(yè)。許多語言實現(xiàn)了一種并發(fā)開發(fā)模式,通常稱之為Actor模型。在這種模型下,進程間傳遞消息,而不是共享狀態(tài),從而消除線程阻塞。
函數(shù)式語言的另一大寶貴優(yōu)點就是簡潔。在Stuart Halloway的《Programming Clojure》一書第一章中,Stuart展示了3行clojure代碼,這比用Jakarta Commons框架開發(fā)減小了三分之一的代碼量,同時還體現(xiàn)出更清晰明了的邏輯思路。
有一個很重要的觀點就是,函數(shù)式語言不是用來取代面向過程或者面向?qū)ο蟮木幊陶Z言的。看看我們在上一節(jié)中所列舉出來的幾種函數(shù)式語言,就會發(fā)現(xiàn)許多新的函數(shù)式語言都是多范型(multi-paradigm),很多時候這些語言都是運行在虛擬機上,并且作為其它面向?qū)ο笳Z言和命令式語言的橋梁出現(xiàn)的。選擇適合手頭工作的語言才是最重要的。我希望從業(yè)者們在開發(fā)主流應用時繼續(xù)使用Java,Groovy或者C#這些通用語言,但當面臨著一個極為復雜的算法或需要實現(xiàn)高并發(fā)時,最好還是轉(zhuǎn)而用函數(shù)式語言來集成這些方案。這也正是Neal Ford說了多年的 “多語言程序員”(polyglot programmer)。對于此類程序員的形成,我們可以參考一下一位Java兼Scala開發(fā)者的學習歷程。
幾種典型的函數(shù)式語言
當我們回顧歷史上的編程語言時,就會發(fā)現(xiàn)其實函數(shù)式語言并不是一個新生事物,它早就出現(xiàn)過。其中最廣為人知的幾種“祖父”級語言包括:LISP和FORTRAN 。自1980年代中期以來,這些語言在企業(yè)和商業(yè)開發(fā)領(lǐng)域逐漸讓位于面向?qū)ο蟮拈_發(fā)語言,流行領(lǐng)域也逐漸縮小到只剩下學術(shù)界。不過下面列出的這幾種函數(shù)式語言最近正在向商業(yè)領(lǐng)域發(fā)起反攻:
◆Erlang:這是一種以A.K Erlang的名字命名的通用并行編程語言。它有函數(shù)式語言的元素,以及一個Actor 并發(fā)模型,從而簡化并行開發(fā)工作。編輯推薦對Erlang感興趣的讀者閱讀一下51CTO以前的一次訪談:因并發(fā)而生 因云計算而熱:Erlang專家訪談實錄。
◆Haskell:這是一門已經(jīng)有超過20年歷史的開源編程語言,它的設計宗旨就是成為一門純粹的函數(shù)式語言。
◆OCaml:面向?qū)ο蟮腃aml(Objective Caml)是Caml語言的一個開源版本,Caml語言可以算是ML語言的一個方言版了,ML語言1970年就已經(jīng)開發(fā)出來了,也是作為一種通用函數(shù)式語言存在的。它被認為是后來出現(xiàn)的F#等多種函數(shù)式語言的基礎。
◆Lisp:表處理語言(List Processing Language)是一種函數(shù)式語言,最初是于1958年擬定的。由它派生出了許多分支。
◆Scala:Scala 語言的設計目標是在Java虛擬機上實現(xiàn)函數(shù)式和面向?qū)ο筮@兩類編程語言的集成。它是一種強類型的編程語言。Scala編程語言近年來的流行度在不斷提升,編輯推薦讀者參閱51CTO的Scala編程語言專題。
◆Clojure:Clojure是Lisp語言的一個現(xiàn)代分支,它運行在Java虛擬機上,是為并發(fā)程序開發(fā)設計的。它是一種動態(tài)類型編程語言。
◆F#:這是一種運行在.Net CLR平臺上的新語言。它是OCaml的一個分支,它兼具了函數(shù)式和命令式面向?qū)ο笳Z言的特點。同時它也是一種強類型的編程語言。F#在未來的.NET平臺上有重要的作用,將在Visual Studio 2010中被正式包含。
值得注意的是函數(shù)式語言并不一定要是動態(tài)語言(dynamic language)。函數(shù)式語言允許動態(tài)或靜態(tài)類型。這里所列出的語言只是各種各樣函數(shù)式語言中的一個子集,每一種實現(xiàn)了某種特定的需求。本文將介紹好幾種典型函數(shù)式語言,而不是專門講解某一種語言。另外我們還有一個沒有回答的問題就是:為什么現(xiàn)在對函數(shù)式語言的需求越來越強烈?
#p#
函數(shù)式語言的特色
函數(shù)式語言的根本宗旨之一就是它不是一種命令式(imperative)語言。在命令式語言中,函數(shù)中定義的變量通常都代表內(nèi)存中的一塊特定大小的區(qū)域,而且賦給它的值也通常允許在整個方法中改變。而在函數(shù)式語言中,對變量的賦值是綁定性的,就像在數(shù)學函數(shù)式中那樣。比如說,有這樣的數(shù)學式:let x=2。這就是說對于這個問題,x的值為2。x的值不能改變,總是2。按照這樣的模式,我們平常編程過程中的一些寫法就沒有意義了,例如這個賦值語句:let x=x+1。在命令式語言中這是有意義的,但是在數(shù)學上,這是沒有任何意義的,因為x=x+1是無解的。理解這個概念后,函數(shù)式開發(fā)(functional development)就算是上路了。
和在數(shù)學中一樣,函數(shù)式語言中的賦值并不僅限于數(shù)值型。方法在函數(shù)式語言中是最為重要的。因此,一個方法閉包(method closure)可以用來給變量賦值,并且被傳遞或調(diào)整到其它的函數(shù)表達式里。用數(shù)學表達式來說就相當于:let x=f(y)。數(shù)學上稱之為:x是以y為自變量的函數(shù)f 的函數(shù)值。任給一個y值,都有一個對應的x值。這就是函數(shù)式編程的另一個核心思想。只要y不變,那么x也總是一個特定的對應值,不會發(fā)生改變。
雖然不同的函數(shù)式語言之間有一些不同之處,但是他們都有以下一些共同點:
◆函數(shù)閉包支持
◆高階函數(shù)
◆用for流程來實現(xiàn)遞歸
◆沒有副作用(side-effects)
◆把重點放在“要計算什么”,而不是“如何去計算”上。
◆引用透明性(Referential transparency)
函數(shù)式語言的功能和術(shù)語
伴隨著函數(shù)式語言的發(fā)展,涌現(xiàn)了許多新的術(shù)語,但是沒有哪種能比Lambda產(chǎn)生得更快。就像我們前面提到的一樣,函數(shù)式編程和數(shù)學界有很大的聯(lián)系。Lambda指的是λ演算(lambda calculus 或 l-calculus)λ演算是一套用于研究函數(shù)定義、函數(shù)應用和函數(shù)遞歸的系統(tǒng)。

清單1 :一個簡單的Lambda表達式
還有許多的λ表達式我們這里都不再深入討論了。如清單1所示的幾個簡單表達式,λ提供了一種全新的語法。上面所舉的例子表示的是一個一元函數(shù),這意味著函數(shù)只需要一個參數(shù),或者說元數(shù)是1.在清單2中,我們可以看到把一個函數(shù)作為另一個函數(shù)的參數(shù)。
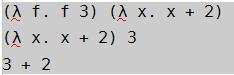
清單2 :一個簡單的λ函數(shù)作參數(shù)傳遞
λ表達式在線指引上對這些有詳細解釋。在清單2中,每行表達式都是等價的。x的函數(shù)被當作參數(shù)傳遞給函數(shù)f,并且作用在3上。函數(shù)x作用在3上就得到了3+2。在函數(shù)式語言里,把一個函數(shù)作用在另一個函數(shù)上是非常常見的一種做法。下面我們考慮清單3:
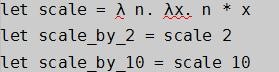
清單3 :用函數(shù)賦值
在清單3中,有3個函數(shù)。函數(shù)scale_by_2是以scale函數(shù)為參數(shù)并且作用在2上。它的返回值就相當于 λ n.x * 2 。這個表達式。函數(shù)式開發(fā)通常就是一層一層地組建這種類型的函數(shù)。
#p#
閉包(Closure)
函數(shù)式語言的另一個重要術(shù)語和關(guān)注點就是閉包。閉包在現(xiàn)在的各種編程語言中都很常見,這個術(shù)語常用來表示一個方法引用(method reference)或者一個匿名函數(shù)(anonymous function)。技術(shù)上看,閉包就是動態(tài)分配的一個含有代碼指針(code pointer)的數(shù)據(jù)結(jié)構(gòu),這個代碼指針指向一個計算函數(shù)結(jié)果的代碼片段以及一個受限變量(found variable)環(huán)境。閉包用來把一個函數(shù)和“私有”變量聯(lián)系起來。許多語言里的匿名函數(shù)就是用來實現(xiàn)這一目的的,這也常常是讓初學者看不懂的地方。
- Function powerFunctionFactory(int power) {
- int powerFunction(int base) {
- return pow(base, power);
- }
- return powerFunction;
- }
- Function square = powerFunctionFactory (2);
- square(3); // returns 9
- Function cube = powerFunctionFactory (3);
- cube(3); // returns 27
在清單4里,factory這個函數(shù)返回的是一個求冪次的函數(shù)。當我們調(diào)用square函數(shù)時,它所需要的power這個變量根本就不在作用域內(nèi),為什么這樣也有意義呢?powerFunctionFactory這個函數(shù)返回后按理來說它的堆棧應該也就隨之釋放了。cube函數(shù)也有相同的問題,只不過它求的冪次不一樣。要實現(xiàn)這樣的語法要求這種語言必須保存變量值,并且要為所創(chuàng)建的每個函數(shù)保存變量值。這就稱為閉包。
閉包允許把自定義的行為作為函數(shù)參數(shù)傳遞,這就引出了另一個重要的術(shù)語,“柯里化”(currying)。
柯里化(Currying)
柯里化這個名字聽起來很深奧,實際上它指的就是把一個多參數(shù)函數(shù)轉(zhuǎn)換成只需要單個參數(shù)的函數(shù)鏈的這種變換。因此,考慮一個函數(shù) foo(x, y) 它的結(jié)果是 z 的值,或者我們把它寫成 foo(x, y) -> z 。現(xiàn)在,我們得把它分解成多個函數(shù),每個函數(shù)都需要一個函數(shù)作為傳入?yún)?shù)或者返回值。看出來這種技術(shù)與λ演算之間的關(guān)系了嗎?
如果有 bar(x)->baz, baz(y)->z。這表示bar函數(shù)將以x為參數(shù)并且返回函數(shù)baz。然后當baz以y為參數(shù)時,它的結(jié)果就是z。因此,foo(x, y) -> z可以用如下方式表示:
bar(x) -> baz
baz(y) -> z
還是讓我們結(jié)合一個C#實例看看吧。下面這段代碼在C# 3.5里是正確的:
- Func< int, Func< int,int>> scale =
- x => y => x * y;
- var scaleBy2 = scale(2);
- scaleBy2 (100);
按正常做法,我們應該編寫一個方法,以數(shù)值100和倍數(shù)2為參數(shù)。但是,采用函數(shù)式編程的方法,函數(shù)scale(2)返回一個可以用來給變量賦值的函數(shù)。我們把那個返回的函數(shù)稱為scaleBy2,當然這很容易“鏈式”地進行下去。通過對一個函數(shù)引用進行命名,我們就有了一個可以被調(diào)整至整個程序里面使用的函數(shù)了。如果你沒有搞清楚這些,沒有關(guān)系,我們下面將繼續(xù)探討函數(shù)式編程的基礎。
數(shù)據(jù)結(jié)構(gòu)
函數(shù)式語言中的數(shù)據(jù)結(jié)構(gòu)包括元組(tuples)和單體(monad)。元組是不可改變的對象序列。序列,鏈表和樹也是函數(shù)式語言中非常常見的數(shù)據(jù)結(jié)構(gòu)。大部分的語言都提供對這些數(shù)據(jù)結(jié)構(gòu)的運算符和庫,以簡化對它們的運算。
一個單體是一個用來反映控制流程或者運算的抽象數(shù)據(jù)類型。引入它的目的是為了避免使用可能帶來副作用(side effect)的語法來表達輸入輸出操作和狀態(tài)變化。
模式匹配(Pattern Matching)
模式匹配并不是函數(shù)式編程的創(chuàng)新,也不是專用于函數(shù)式編程。但是它和函數(shù)式語言有廣泛聯(lián)系,因為其它主流編程語言大都沒有這一特性。模式匹配說白了就是一種對值或者類型進行匹配的簡潔方法。如果你曾經(jīng)寫過很復雜的if,if/else,或者switch語句,那么你應該已經(jīng)能認識到模式識別的價值了。清單6是一個用Mathematica編寫的匹配程序,用于求一個斐波納契序列(Fibonacci sequence)。
- fib[0|1]:=1
- fib[n_]:= fib[n-1] + fib[n-2]
清單6 :用Mathematica寫的模式匹配范例
對0或1進行匹配的結(jié)果是1.對其它任何數(shù)的匹配都會進入fid這個遞歸調(diào)用里。要想找一個比這還簡潔的求斐波納契序列的方法可真是不容易了。這是一種非常強大的技術(shù)。
原文:An Introduction to Functional Languages
作者:Ken Sipe
【相關(guān)閱讀】































