循環變換器中的潛在思維:深度與參數效率的權衡研究
研究背景與創新點
深度學習模型,尤其是大型語言模型(LLMs)在推理任務上的表現令人矚目。傳統觀點認為,模型參數量是決定推理能力的主要因素。然而,Google Research團隊的這項研究《推理潛在思維:循環變換器的力量》提出了一個更為大膽的觀點:許多推理問題主要需要的是足夠的深度,而非海量參數。該研究探索了循環變換器(Looped Transformers)在推理任務中的應用潛力,并揭示了模型架構與推理能力之間的深層聯系。
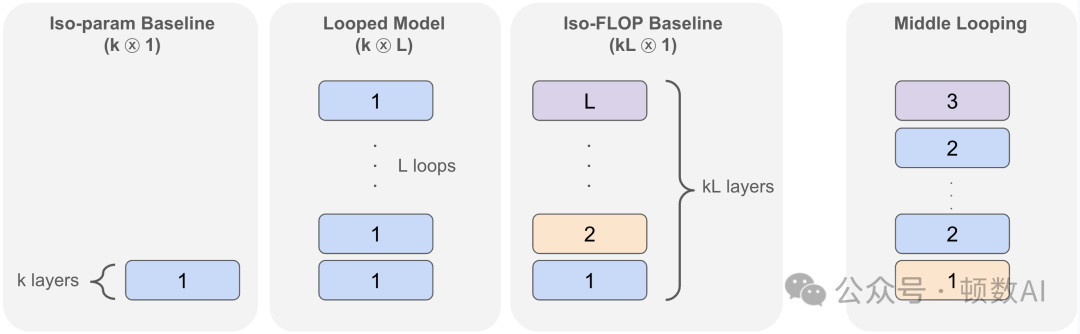
本文的核心創新點在于提出并驗證了循環模型在推理任務上的優勢。研究表明,一個k層變換器循環L次(表示為(k?L))的性能可以接近甚至超過具有相同計算量但參數量大L倍的非循環kL層模型,同時顯著優于參數量相同的k層非循環模型。這一發現不僅適用于合成推理問題,還擴展到了實際語言建模場景,揭示了模型架構設計中的重要權衡。
研究方法與實驗設計
研究團隊采用了多種方法驗證其假設,包括:
- 合成推理任務實驗:研究者設計了三類合成推理任務來測試循環模型的能力:
- n元加法:測試模型對多個三位數進行加法的能力
- p-hop歸納:測試模型在序列中進行多步回溯檢索的能力
- i-GSM(合成小學數學問題):模擬小學數學應用題的計算圖問題
- 語言建模實驗:在Pile數據集上預訓練1B參數規模的模型,比較不同架構在下游任務上的表現:
- 閉卷問答(測試記憶能力)
- 開卷問答(測試閱讀理解能力)
- 數學應用題(測試數學推理能力)
- 推理原語(測試基礎推理能力)
- 理論分析:證明循環模型在特定推理任務上的表達能力,包括:
- 群組合問題的最優深度解
- 循環模型模擬非循環模型的能力
- 循環模型與思維鏈(Chain-of-Thought)推理的關系
實驗設計精巧,通過比較(k?L)循環模型與兩個基線:參數量相同的(k?1)模型和計算量相同的(kL?1)模型,全面評估了循環架構的優勢與局限。
主要研究發現
1. 循環模型在合成推理任務上的表現
在合成推理任務上,循環模型展現出顯著優勢。以n元加法為例,即使是循環12次的1層網絡,其表現也接近使用12倍參數量的12層基線模型。類似地,在p-hop問題和i-GSM任務上,循環模型也能以少得多的參數達到與非循環模型相當的性能。這表明這些推理任務主要需要的是足夠的深度,而非大量參數。
研究者還通過理論分析證明,對于群組合問題,一個1層變換器循環log?(n)次就能有效解決,這與非循環模型的最佳已知深度上界相匹配。
2. 循環模型在語言建模中的歸納偏置
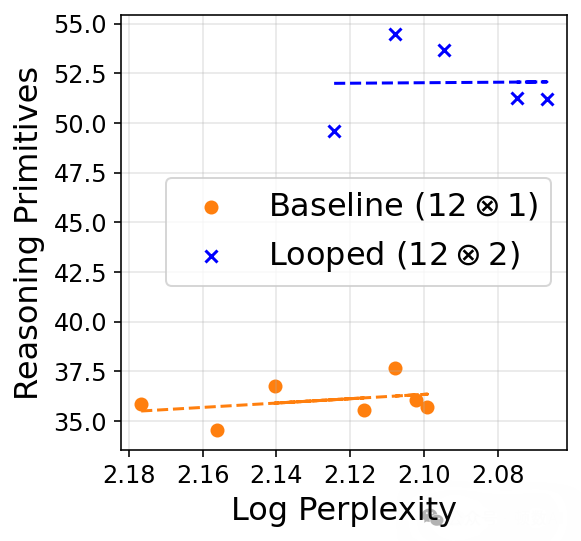
在語言建模實驗中,研究者發現了一個有趣的現象:雖然循環模型的困惑度(perplexity)不如參數量更大的非循環模型,但在需要推理的下游任務上表現出色。具體而言:
- 在記憶型任務(如閉卷問答)上,循環模型的優勢有限
- 在推理型任務(如開卷問答、數學應用題)上,循環模型能彌補大部分與參數量更大模型的差距
- 在純推理原語任務上,循環模型甚至超過了參數量更大的基線模型
這表明循環架構具有促進推理能力的歸納偏置,即使以犧牲一些記憶能力為代價。研究者通過"等困惑度"下游性能比較(isoplots)進一步驗證了這一發現。
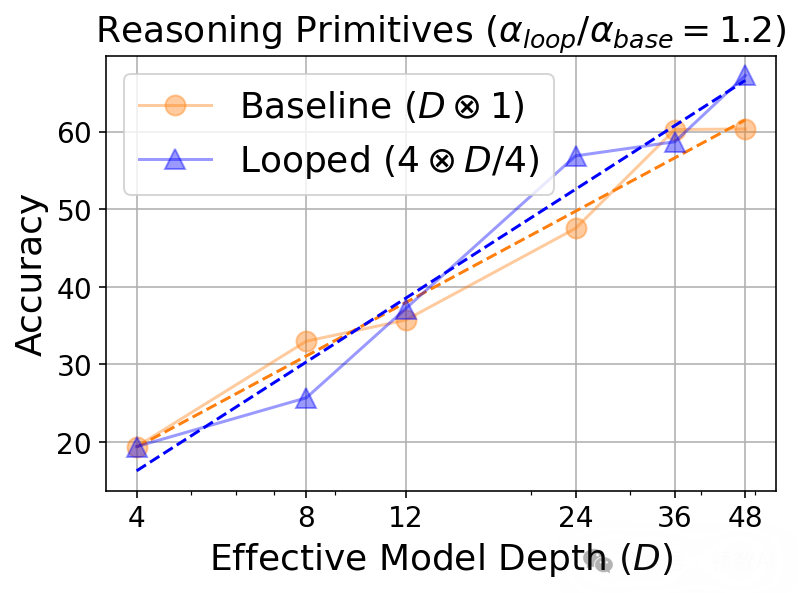
3. 循環深度的縮放行為
研究發現,隨著循環次數增加,模型在各類任務上的表現呈現對數縮放規律:
準確率 = α·log(D) + β其中D為有效深度,α衡量深度對下游性能的影響。不同任務類型的α值不同,推理任務的α值相對更高,表明推理任務從深度增加中獲益更多。這種縮放行為類似于思維鏈(CoT)推理的推理時間縮放。
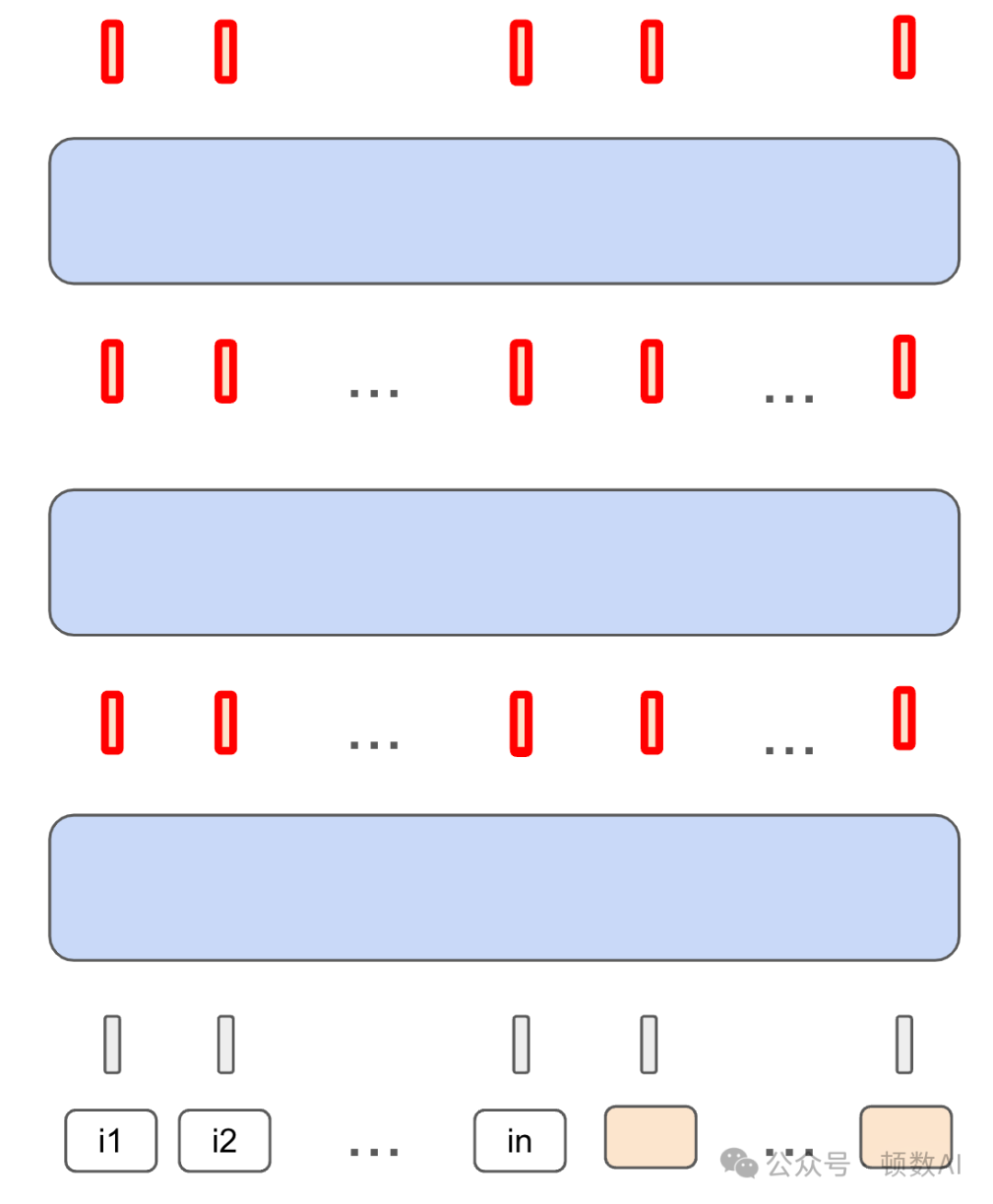
4. 循環模型與思維鏈推理的聯系
研究者提出了循環模型與思維鏈推理之間的理論聯系。思維鏈推理可以視為一種特殊的循環模型,每次迭代產生一個思維token。而循環模型則更為強大,能在每次迭代中生成多個"潛在思維"。研究者證明了循環變換器能夠模擬思維鏈推理,這解釋了為何循環模型在推理任務上表現出色。
5. 基于循環的正則化方法
基于循環模型對推理的歸納偏置,研究者設計了一種新的正則化方法,通過鼓勵模型層之間的相似性來獲得循環模型的優勢,同時保持非循環模型的靈活性。實驗表明,這種正則化方法能在不影響困惑度的情況下提升模型的推理能力。
技術細節分析
循環變換器的數學表示
循環變換器可以形式化表示為重復應用相同的變換器塊。給定L層變換器塊TB,循環T次的模型可表示為:
p_{θ,T} = OUTPUT ° (TB)^T ° EMBED其中OUTPUT是輸出層,EMBED是嵌入層,(TB)^T表示變換器塊循環應用T次。
理論結果
研究提供了幾個重要的理論結果:
- 群組合定理:對于任何有限群G和n個元素,存在一個1層變換器循環?log?n?次就能計算這n個元素的組合,且深度最優。
- 循環模型模擬定理:具有R個不同層的L層非循環變換器可以被一個循環L次的1層變換器模擬,后者的嵌入維度增加R+2,MLP隱藏維度增加O(L)。
- CoT模擬定理:任何L層非循環變換器進行m步CoT推理,都可以被一個具有L+O(1)層、循環m次的變換器模擬。
這些理論結果為實驗觀察提供了堅實的數學基礎,證明了循環架構在推理任務上的優勢并非偶然。
實現細節
研究中使用的循環變換器實現相對簡單,主要是在前向傳播中重復應用相同的變換器塊。對于(k?L)模型,即k層變換器循環L次,總共有k×L層計算,但只有k層的參數。
研究還探索了"中間循環"(Middle Looping)變體,即保留網絡開始和結束的獨立層,只在中間部分應用循環。這種方法在某些任務上表現更好,表明網絡的不同部分可能需要不同程度的參數共享。
研究意義與局限性
研究意義
- 參數效率提升:研究表明,通過循環架構可以顯著減少模型參數量,同時保持甚至提升推理能力,這對于資源受限場景具有重要價值。
- 推理與記憶的二分法:研究揭示了模型能力中推理與記憶的權衡,為理解大型語言模型的能力提供了新視角。
- 與思維鏈的聯系:建立了循環架構與思維鏈推理之間的理論聯系,為理解和改進推理機制提供了新思路。
- 正則化方法:提出的基于循環的正則化方法為提升模型推理能力提供了實用工具。
局限性
- 推理定義的模糊性:研究中"推理"的定義相對寬泛,不同類型的推理可能需要不同的模型架構。
- 任務覆蓋有限:實驗主要集中在特定類型的推理任務,可能不能完全代表所有推理場景。
- 規模限制:實驗主要在1B參數規模進行,更大規模模型的行為可能有所不同。
- 計算效率權衡:雖然參數量減少,但循環架構在推理時的計算量與非循環模型相同,沒有提高推理速度。
未來研究方向
- 多模態推理:探索循環架構在視覺-語言等多模態推理任務中的應用。
- 推理形式化:更精確地形式化不同類型的推理問題,理解它們對模型架構的不同需求。
- 推理時間縮放:進一步探索利用循環模型進行更高效的推理時間縮放,輔助更深層次的推理。
- 混合架構:結合循環和非循環層的混合架構,平衡推理能力和記憶能力。
- 更優循環策略:研究不同的循環策略(如選擇性循環、動態循環等)對性能的影響。
結論
本研究對循環變換器在推理任務中的應用進行了深入探索,揭示了一個重要發現:許多推理問題主要需要的是計算深度而非大量參數。循環架構通過參數共享實現了深度增加而不增加參數量,在各種推理任務上展現出顯著優勢。研究還建立了循環模型與思維鏈推理之間的理論聯系,為理解大型語言模型的推理機制提供了新視角。
這些發現不僅有理論意義,還提供了實用價值:通過循環架構或基于循環的正則化,可以構建更參數高效的推理模型。未來研究可進一步探索循環架構在更廣泛推理任務中的應用,以及與其他推理增強技術的結合。
總的來說,這項研究為大型語言模型的架構設計提供了新的思路,強調了在追求更強推理能力時,深度與參數量之間的權衡,以及循環架構作為一種有效折中方案的潛力。
論文:https://arxiv.org/abs/2502.17416

















